| Feladat: | Pontversenyen kívüli P.159 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bacsó Gábor , Csendes Tibor , Dobor T. , Emese Gy. , Horváth Mária , Kiss E. , Kollár János , Krebsz Sarolta , Lelkes A. , Markó P. , Páles Zsolt , Pócsi György , Révész György , Surján P. , Vörös Z. | ||
| Füzet: | 1974/március, 115 - 116. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Logikai feladatok, Mozgással kapcsolatos szöveges feladatok, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1972/december: Pontversenyen kívüli P.159 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A közlés szerint a teknőc átlagos sebessége (m/perc) volt, viszont a b) és c) feltételek szerint minden megfigyelő (m/perc) átlagsebességet észlelt, és az a) feltétel szerint ezek a figyelések lefedték a teknőc egész mozgását. Ezek azonban csak első látásra vannak ellentmondásban, ugyanis a megfigyelők száma nincs korlátozva. 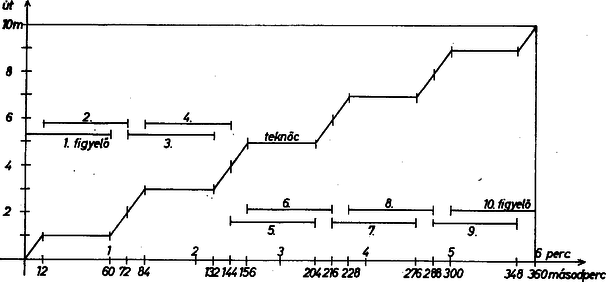 Ábránk a minimálisan szükséges megfigyelővel mutat egy lehetőséget a történet idő-út grafikonjára, az út egyes métereiben egyenletes mozgást tételezve fel. Megjegyzések. 1. A feladat "nehézsége'' kizárólag abban áll, hogy ki kellett lépnünk a jól ismert mozgástípusok köréből. 2. A feltételek nem zárják ki azt, hogy az egyes megfigyelők több részletben teljesítsék 1-1 percüket. Ha ezt megengedjük, a teknőc tetszőlegesen nagy utat is megtehet, a perces menetidő megtartásával: az első másodperc alatt áll, és ezt ember figyeli, ezután mindegyik ember kizárólagos, mp-nyi figyelése alatt 1-1 métert halad, együttvéve métert. Itt és kapcsolatát a egyenlet adja meg. ‐ Megmagyarázható a mozgás akkor is, ha a megteendő út mértékszáma nem természetes szám. |