Kezdőlap


Feladat:	Pontversenyen kívüli P.151	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos Tamás , Kiss Emil
Füzet:	1973/február, 75 - 77. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Integrálszámítás, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1972/október: Pontversenyen kívüli P.151

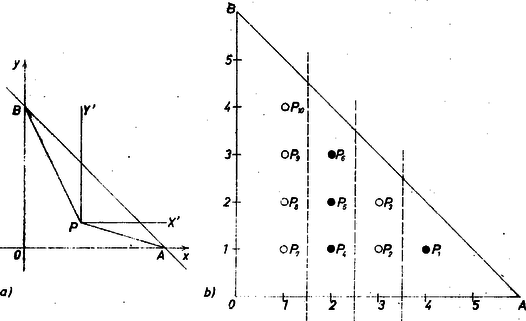
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $O A B$ háromszög egy belső pontja $P$ , és az ezen át az $x$ , $y$ tengely pozitív felével párhuzamos félegyenes $P X'$ , ill. $P Y'$ (1 a ábra).

Ekkor a látószög mint a

P B, P A

félegyenesek irányszögének különbsége

\begin{matrix} A P B ∢ = X' P B ∢ - X' P A ∢ = π / 2 + Y' P B ∢ + A P X' ∢, \end{matrix}

ennek

φ

középértékét kell kiszámítanunk háromszögünk

P_{1}, P_{2}, ..., P_{10}

rács-pontjaira (1 b ábra):

\begin{matrix} φ = \frac{π}{2} + \frac{1}{10} \sum_{i = 1}^{10} (Y' P_{i} B ∢ + A P_{i} X' ∢) = \frac{π}{2} + \frac{2}{10} \sum_{i = 1}^{10} A P_{i} X' ∢, \end{matrix}

ugyanis alakzatunk (a háromszög és a benne levő rácspontok halmaza) szimmetrikus az

y = x

egyenesre, ennek alapján a zárójel kétféle tagjából képezett összegek egyenlők.
A szögeket célszerű tangensük alapján mindjárt ívmértékben kiírni:^{$^{*}$}

\begin{matrix} i & tgA P_{i} X' ∢ = t_{i} & arc tg t_{i} & Közép \\ 1 & 1 / 2 = 0,5 & 0,4636 & 0,4636 \\ 2 & 1 / 3 = 0,3333 & 0,3217 \\ 3 & 2 / 3 = 0,6667 & 0,5880 & 0,4578 \\ 4 & 1 / 4 = 0,25 & 0,2450 \\ 5 & 2 / 4 = 0,5 & 0,4636 \\ 6 & 3 / 4 = 0,75 & 0,6435 & 0,4542 \\ 7 & 1 / 5 = 0,2 & 0,1974 \\ 8 & 2 / 5 = 0,4 & 0,3805 \\ 9 & 3 / 5 = 0,6 & 0,5404 \\ 10 & 4 / 5 = 0,8 & 0,6747 & 0,4518 \end{matrix}

A táblázat utolsó oszlopa az

i = 1,3,6,10

határokig bezárólag kapott ívmértékszámok középértékét tünteti fel. Közülük az utolsó a feladat eredeti kérdésére vonatkozik, az első három pedig a megfelelő eredmény

O A = 3,4

, ill.

5

esetére. Eszerint (

3

tizedesre kerekítve)

\begin{matrix} φ & = (φ_{6} =) \frac{π}{2} + 2 \cdot 0,4518 = 2,474, \\ φ_{3} & = 2,498, φ_{4} = 2,486, φ_{5} = 2,479, \end{matrix}

míg a közölt érték:

π - log 2 = 3,1416 - 0,6931 = 2,4484 ...

, ezt

φ_{6}

alig többel, mint

1 %

-kal haladja meg.

Megjegyzés. A

P_{1}

-hez; a

P_{2}

-höz és

P_{3}

-hoz; a

P_{4}

-hez,

P_{5}

-höz és

P_{6}

-hoz; valamint a

P_{7}

P_{8}

P_{9}

P_{10}

pontokhoz tartozó átlagok, külön-külön egy-egy (szokásos) közelítést adnak az

\begin{matrix} \int_{0}^{1} arc tg x \end{matrix}

integrálra. Nem egészen szabályos felső közelítések ezek, hiszen az utolsó, az

x = 1

osztásponthoz tartozó függvényérték nem szerepel az átlagban. Azt mondhatjuk, véletlen, hogy még így is felső közelítést kaptunk. Mindenesetre, ha a beosztást finomítjuk, a mondott integrál értékét egyre pontosabban kapjuk meg, tehát e közelítő értékek súlyozott átlaga is tart az integrál értékéhez. Ennek az integrálnak a fenti számítás alapján kapott felső közelítő értékeit és a trapéz-szabályból kapott alsó közelítő értékeit az alábbi táblázatban foglaljuk össze:

\begin{matrix} n & Felső közelítés & Alsó közelítés \\ 2 & 0,4636 & 0,4282 \\ 3 & 0,4548 & 0,4341 \\ 4 & 0,4507 & 0,4362 \\ 5 & 0,4482 & 0,4371 \end{matrix}

Ha tudjuk, hogy az

\begin{matrix} F (x) = x arc tg x - \frac{1}{2} log (1 + x^{2}) \end{matrix}

függvény deriváltja épp

arc tg x

aminek az ellenőrzéséhez a tanult deriválási szabályokon kívül csak az iskolai táblázatban is megtalálható

\begin{matrix} (arc tg x)' = \frac{1}{1 + x^{2}}, (log x)' = \frac{1}{x} \end{matrix}

deriváltakat kell ismernünk), a fenti integrált pontos értékét is meghatározhatjuk a Newton-Leibniz-formula szerint:

\begin{matrix} \int_{0}^{1} arc tg x \end{matrix}

A feladatban közölt átlagos látószöget a fenti megoldás szerint ebből úgy kapjuk, hogy a kétszereséhez hozzáadjuk a

π / 2

szöget, így valóban a

(π - log 2)

számot kapjuk.

^{$^{*}$}Az iskolai függvénytáblázat-gyűjtemény 8. sz. táblázata.