Kezdőlap


Feladat:	Pontversenyen kívüli P.148	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bacsó Gábor , Bara T. , Császár Gy. , Iszlay Zoltán , Kollár János , Kópházi József , Páles Zsolt , Pallagi Dezső
Füzet:	1973/október, 72 - 76. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Transzverzálisok, Kör egyenlete, Körök, Szabályos tetraéder, Szabályos sokszögek geometriája, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1972/szeptember: Pontversenyen kívüli P.148

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. A feladatot a koordináta-geometria eljárásaival oldjuk meg. Vegyük origónak $K$ -t, az $x$ tengelyt $B C$ -vel párhuzamosnak, irányítsuk az $y$ tengelyt úgy, hogy $A$ -n, a pozitív fele menjen át és válasszuk hosszúságegységnek a $K A$ szakasz felét. Így a csúcsok: $A (0; 2), B (- \sqrt[]{3}; - 1), C (\sqrt[]{3}; - 1)$ . Legyen másrészt az $e$ metsző egyenes egyenlete $y = m x$ , ahol a föltevések szerint egyrészt $m$ véges és $m \neq \pm 1 / \sqrt[]{3}$ , másrészt ‐ mivel $A_{1}$ , $B_{1}$ , $C_{1}$ mindegyike létrejött, $e$ nem párhuzamos, egyik oldallal sem ‐, ezért $m \neq 0$ és $m \neq \pm \sqrt[]{3}$ (ugyanis ezek háromszögünk oldalegyeneseinek iránytangensei, 1. ábra).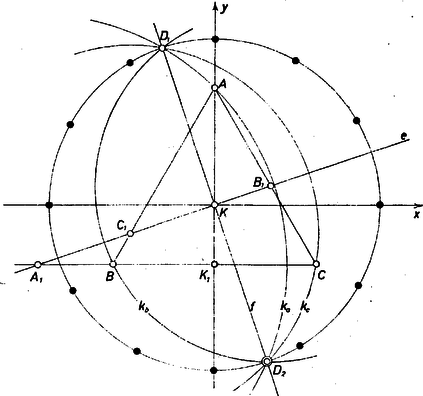

1. ábra

B C

C A

A B

oldalegyenes egyenlete rendre

y = - 1

y = \mp \sqrt[]{3} x + 2

, és

e

-vel való metszéspontjaik koordinátái:

\begin{matrix} A_{1} (- \frac{1}{m}, - 1), B_{1} (\frac{2}{m + \sqrt[]{3}}, \frac{2 m}{m + \sqrt[]{3}}), C_{1} (\frac{2}{m - \sqrt[]{3}}, \frac{2 m}{m - \sqrt[]{3}}) . \end{matrix}

B_{1}

pont körüli,

B

-n átmenő

k_{b}

kör egyenlete:

\begin{matrix} {(x - \frac{2}{m + \sqrt[]{3}})}^{2} + {(y - \frac{2 m}{m + \sqrt[]{3}})}^{2} = {(- \sqrt[]{3} - \frac{2}{m + \sqrt[]{3}})}^{2} + {(- 1 - \frac{2 m}{m + \sqrt[]{3}})}^{2} \end{matrix}

(a jobb oldalt abból kapjuk, hogy a bal oldal értéke mindig annyi, mint amennyi akkor adódik, ha

x

y

helyére

B

koordinátáit írjuk), rendezve

\begin{matrix} K_{b} (x, y) = x^{2} + y^{2} - \frac{4}{m + \sqrt[]{3}} (x + m y) - 8 = 0. \end{matrix}

(1)

Hasonlóan a

C_{1}

körüli,

C

-n átmenő

k_{c}

, kör, végül az

A_{1}

körüli,

A

-n átmenő kör egyenlete:

\begin{matrix} K_{c} (x, y) & = x^{2} + y^{2} - \frac{4}{m - \sqrt[]{3}} (x + m y) - 8 = 0, & (2) \\ K_{a} (x, y) & = x^{2} + y^{2} + \frac{2}{m} (x + m y) - 8 = 0. & (3) \end{matrix}

2. Azt kell bebizonyítanunk, hogy a

k_{b}

k_{c}

, körök

D_{1}

D_{2}

metszéspontjain a

k_{a}

kör is átmegy.

D_{1}

és

D_{2}

koordinátái kielégítik a

K_{b} (x, y) = 0

és

K_{c} (x, y) = 0

. egyenleteket, ezért bármely két,

λ_{b}

λ_{c}

állandó számot véve, a

\begin{matrix} λ_{b} \cdot K_{b} (x, y) + λ_{c} \cdot K_{c} (x, y) = (λ_{b} + λ_{c}) (x^{2} + y^{2} - 8) - & (4) \\ - 4 (\frac{λ_{b}}{m + \sqrt[]{3}} + \frac{λ_{c}}{m - \sqrt[]{3}}) (x + m y) = 0 \end{matrix}

egyenletet is. Mármost az állítást annak megmutatásával bizonyítjuk, hogy, ez az egyenlet

λ_{b}

, és

λ_{c}

alkalmas megválasztásával azonossá tehető

k_{a}

egyenletével. (4) azonos a (3)-mal, ha van olyan

λ_{b}

és

λ_{c}

, hogy bennük

(x^{2} + y^{2} - 8)

és

(x + m y)

együtthatói rendre egyenlők:

\begin{matrix} λ_{b} + λ_{c} = 1, \\ - 4 (\frac{λ_{b}}{m + \sqrt[]{3}} + \frac{λ_{c}}{m - \sqrt[]{3}}) = \frac{- 4 m (λ_{b} + λ_{c}) + 4 \sqrt[]{3} (λ_{b} + λ_{c})}{m^{2} - 3} = \frac{2}{m} . \end{matrix}

Az utóbbiból az első fölhasználásával és kellő alakításával

\begin{matrix} λ_{b} - λ_{c} = \frac{1}{4 \sqrt[]{3}} [\frac{2 (m^{2} - 3}{m} + 4 m] = \frac{\sqrt[]{3}}{2} (m - \frac{1}{m}), \end{matrix}

tehát a kívánt értékek:

\begin{matrix} λ_{b} = \frac{1}{2} + \frac{\sqrt[]{3}}{4} (m - \frac{1}{m}), λ_{c} = \frac{1}{2} - \frac{\sqrt[]{3}}{4} (m - \frac{1}{m}) . \end{matrix}

[Pl.

λ_{b}

csak

m = + \frac{1}{\sqrt[]{3}}

és

m = \sqrt[]{3}

mellett lehetne 0, ekkor

λ_{c} = 1

és

K_{c} (x, y) \equiv K_{a} (x, y)

C_{1} \equiv A_{1} \equiv B

, ami kizárt eset.]
Ezzel a feladat állítását bebizonyítottuk ‐ anélkül, hogy

D_{1}

D_{2}

koordinátáit meghatároztuk és

k_{a}

-ba helyettesítettük volna.
3. Most kiszámítjuk

D_{1}

D_{2}

koordinátáit. Vonjuk ki (1)-ből (2)-t:

\begin{matrix} (\frac{4}{m - \sqrt[]{3}} - \frac{4}{m + \sqrt[]{3}}) (x + m y) = \frac{8 \sqrt[]{3}}{m^{2} - 3} (x + m y) = 0, \end{matrix}

amiből (mivel

m \neq \pm \sqrt[]{3}

)

\begin{matrix} x + m y = 0. \end{matrix}

(5)

Innen

y = - x / m

-et (1)-be helyettesítve rövid számítással

D_{1} (x_{1}, y_{1})

és

D_{2} (x_{2}, y_{2})

abszcisszája, ordinátája rendre:

\begin{matrix} x_{1,2} = \pm \sqrt[]{\frac{8 m^{2}}{m^{2} + 1}}, y_{1,2} = \mp \sqrt[]{\frac{8}{m^{2} + 1}} . \end{matrix}

(6)

Eszerint

D_{1}

és

D_{2}

mindig egymás tükörképei

K

-ra nézve. Ezért a koordinátákat

x_{D}

-vel,

y_{D}

-vel jelölve,

m

kiküszöbölésével

\begin{matrix} x_{D}^{2} + y_{D}^{2} = 8, \end{matrix}

tehát a három kör közös pontja ‐ ha létrejön ‐ mindig rajta van az

A B C

háromszög

K

középpontja körüli,

2 \sqrt[]{2} = \sqrt[]{2} K A

sugarú

k_{d}

körön.
4. Fordítva, meg kell vizsgálnunk, kiadódik-e

k_{d}

minden pontja

D

-ként. Eleve tudjuk azonban, hogy az

m

iránytényező kizárt

0

\pm \sqrt[]{3}

\pm 1 / \sqrt[]{3}

értékei mellett (6) eredményeink nem érvényesek. Így pedig nincs olyan megengedett

m

, amely

x_{D} = 0

-ra vezet, tehát

k_{d}

-nek az ordinátatengelyen ‐ a

K A

egyenesen ‐ levő pontjai nem tartoznak hozzá a

h

mértani helyhez. Másrészt olyan

m

sincs (6) szerint, amely

y_{D} = 0

-ra vezetne, tehát

k_{d}

-nek a

K

-n át

K A

-ra merőlegesen (

B C

-vel párhuzamosan) húzott egyenesen levő pontjai sem tartoznak

h

-hoz. Az így kizárt 4 pontból újabb 4 ‐ 4 kizárandó adódik

K

körüli,

120^{\circ}

-kal, illetve

240^{\circ}

-kal való elfordításukkal, hiszen ezek az elfordítások háromszögünket önmagába viszik át. Az újabb 8 pontra az ordináta és az abszcissza hányadosának abszolút értéke

\sqrt[]{3}

, illetve

1 / \sqrt[]{3}

k_{d}

-nek minden más

D

pontjára az

\frac{y_{D}}{x_{D}} = μ

hányados véges és a

0

\pm 1 / \sqrt[]{3}

\pm \sqrt[]{3}

értékektől különböző szám és (5) mutatja, hogy ekkor

- 1 / μ

éppen az az

m

érték, mely a fentiek szerint

D

-t adja a 3 kör közös pontjaiként (és

D

-nek az origóra vonatkozó tükörképét, amelyre a hányados értéke ugyancsak

μ

).
Mindezek szerint a közös pontok mértani helye a

k_{d}

kör, a mondott 12 pont kihagyásával. (E pontok egy szabályos 12-szög csúcsai.)

Bacsó Gábor, Pallagi Dezső

Megjegyzések. 1. A fenti (5) ‐ mint elsőfokú egyenlet ‐ a

k_{b}

k_{c}

, körök

f

közös húregyenesének, hatványvonalának^{$^{*}$} egyenlete. Ugyanez adódik (1) és (3) különbségéből is, tehát

f

k_{b}

k_{a}

körpárnak is hatványvonala. A bizonyítást ezek alapján így is befejezhetjük:

f

csak 2 pontban metszi

k_{b}

-t és azokon áthalad

k_{c}

is,

k_{a}

is.
2. Eleve a pont körre vonatkozó hatványának fogalmát használja fel a következő, a koordinátageometriainál jóval egyszerűbb megoldás.

II. megoldás. Nyilvánvaló, hogy a keresett mértani hely örökli az

A B C

háromszög tengelyes és forgási szimmetriáit. Példaként véve két egymásba így át nem vihető

e

egyenest, azt sejtjük, hogy a keresett mértani hely egy

K

körüli kör (ill. a kizárt helyzetek miatt ennek része); ezt bizonyítjuk.
Legyen a háromszög magasságának hossza

m

, és messe

A K

B C

-t

K_{1}

-ben.

K

-nak

k_{a}

-ra vonatkozó hatványa¹ a

K A_{1} K_{1}

és

A A_{1} K_{1}

derékszögű háromszögek alapján

\begin{matrix} K A_{1}^{2} - A A_{1}^{2} = (K K_{1}^{2} + K_{1} A_{1}^{2}) - (A K_{1}^{2} - K_{1} A_{1}^{2}) = \frac{m^{2}}{9} - m^{2} = - \frac{8}{9} m^{2}, \end{matrix}

állandó, független

e

helyzetétől, tehát ugyanennyi

K

-nak

k_{b}

-re,

k_{c}

,-re vonatkozó hatványa is. Eszerint a

K

-ban

e

-re állított merőlegest mindhárom kör ugyanabban a két pontban metszi (a hatvány negatív értéke miatt

K

mindhárom körben benne van). És ha

e

K

körül forgatva minden megengedett helyzetén átfut, a metszéspont-pár a

K

körül kört ír le, sugarának négyzete egyenlő a hatvány abszolút értékével:

\begin{matrix} K D_{1} \cdot K D_{2} = K D_{1}^{2} = \frac{8}{9} m^{2} . \end{matrix}

III. megoldás. A feladatot térgeometriai értelmezéssel oldjuk meg. Az

A B C

szabályos háromszöget egy

A B C D

szabályos tetraéder alaplapjának vesszük ‐ ekkor

K

D

csúcs merőleges vetülete az alapon ‐, az alakzatunkat származtató

e

egyenest pedig egy a

D K

magasságvonalon átmenő

S

sík és az alapsík metszésvonalának tekintjük. Ekkor

S

a tetraéder

D A B

D B C

D C A

lapsíkját rendre a

D C_{1}

D A_{1}

D B_{1}

egyenesben metszi, és ha

B_{1}

C_{1}

az alapháromszög kerületén vannak, akkor a

D B_{1} C_{1}

háromszög a tetraéder és

S

metszésidoma (2. ábra).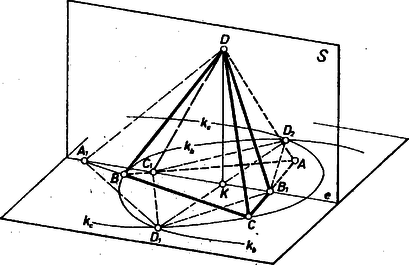

2. ábra

Azt fogjuk belátni ‐ a fenti jelöléseket tovább használva ‐, hogy a

k_{b}

k_{c}

, körök

D_{1}

D_{2}

metszéspontjai azonosak a

D

csúcsnak azokkal az új helyzeteivel, ahová jut, ha a metszésidomot a

B_{1} C_{1}

egyenes mint tengely körül az egyik vagy a másik irányban belefordítjuk az alapsíkba.
Valóban, a

D A C

lapot

A C

körül az alaplapra ráfordítva

D

B

-be jut. S mivel eközben

B_{1}

a helyén marad, a

B_{1} B

sugár egyenlő a metszetidom

B_{1} D

oldalával, és szerkesztésünk szerint

D_{1} B_{1} = D_{2} B_{1} = B B_{1} = D B_{1}

.
A meggondolást megismételve a

D A B

lappal, kapjuk, hogy

D_{1} C_{1} = D_{2} C_{1} = C C_{1} = D C_{1}

, ezek alapján a

D_{1} B_{1} C_{1}

, a

D_{2} B_{1} C_{1}

és a

D B_{1} C_{1}

háromszögek egybevágók, ennélfogva mint e háromszögek megfelelő szakaszaira:

D_{1} K = D_{2} K = D K

, állandó.
Azt kaptuk, hogy a

k_{b}

k_{c}

körök metszéspontjai a metsző egyenes (és az

S

sík) minden megengedett helyzetében azon a

k_{d}

körön adódnak, amelynek középpontja

K

és sugara a tetraéder magassága. Mivel pedig

K D

és vele együtt

K D_{1}

K D_{2}

is merőleges

B_{1} C_{1}

-re, azt is kaptuk, hogy

k_{b}

k_{c}

köreink

D_{1} D_{2}

közös húregyenese mindig átmegy

K

-n.
A

k_{a}

kör amiatt halad át

D_{1}

-en és

D_{2}

-n, mert

D

-t

B C

körül az alapsíkba fordítva,

A

-ba jut, ezért

A_{1} A = A_{1} D

, másrészt

A_{1}

is a

B_{1} C_{1}

egyenes pontja, tehát a metszetidom lefordításával

A_{1} D = A_{1} A

hossza az

A_{1} D_{1}

A_{1} D_{2}

szakaszokban valódi nagyságában látszik. Ezzel a feladat állítását bebizonyítottuk.
Már csak annak a vizsgálata van hátra, hogy a

k_{d}

kör mely pontjai tartoznak hozzá a

h

mértani helyhez. Láttuk, hogy a

D_{1} D_{2}

szakasz

k_{d}

-nek

S

-re, egyszersmind

e

-re merőleges átmérője:

e

-nek minden olyan helyzete figyelembe veendő, mely különböző a

K A

K B

K C

egyenestől is a rájuk

K

-ban állított merőlegestől, tehát a kizárt helyzetek száma 6. Így ki van zárva

h

-ból

k_{d}

-nek az a

6 \cdot 2 = 12

pontja, melyek e 6 kizárt egyenesre merőleges átmérő végpontjai. Fordítva,

k_{d}

-nek minden más

D_{1}

pontjához úgy kapjuk

e

-nek a

D_{1}

-et előállító helyzetét, hogy merőlegest állítunk

K

-ban

K D_{1}

-re. Más kizárt pont tehát nincs.

^{$^{*}$}Lásd pl. Tolnai Jenő: Érdekes matematikai gyakorló feladatok, II. rész. Tankönyvkiadó, Budapest, 1971. 22. old.