Kezdőlap


Feladat:	Pontversenyen kívüli P.147	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Császár Gy. , Fürész B. , Kiss Emil , Kollár János , Kópházi J. , Kozma I. , Oláh Vera , Páles Zs. , Ureczky J.
Füzet:	1973/április, 171 - 172. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1972/szeptember: Pontversenyen kívüli P.147

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $r$ sugarú kör $α$ középponti szögű ívével $(0 < α ≦ 2 π)$ és a végpontjai közti húrral határolt körszelet területe: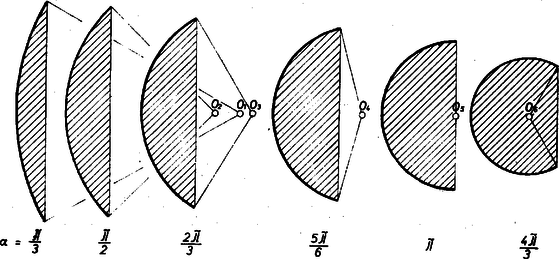

\begin{matrix} T = \frac{1}{2} r^{2} (α - sin α) . \end{matrix}

Válasszuk az adott hosszúságot egységnyinek, azaz

r α = 1

, így

r = \frac{1}{α}

és

\begin{matrix} T (α) = \frac{1}{2} \cdot \frac{α - sin α}{α^{2}} . \end{matrix}

Rögtön látjuk, hogy ez a függvény minden

α \neq 0

helyen deriválható, így ha van maximuma a vizsgált intervallum belsejében, akkor ott

T' (α) = 0

. A derivált, mindjárt alkalmas goniometrikus alakítással:

\begin{matrix} T' (α) = \frac{1}{2 α^{3}} [2 sin α - α (1 + cos α)] = \frac{cos \frac{α}{2}}{α^{3}} \cdot (2 sin \frac{α}{2} - α cos \frac{α}{2}) = \\ = \frac{2 cos^{2} \frac{α}{2}}{α^{3}} (tg \frac{α}{2} - \frac{α}{2}) . \end{matrix}

Az utolsó alak zárójelbeli kifejezése

0 < \frac{α}{2} < \frac{π}{2}

, azaz

0 < a < π

esetében pozitív,

π < α < 2 π

esetén negatív, és mindezekre az értékekre az első tényező pozitív. Eszerint

0 < α < π

esetén

T' (α) > 0

, viszont

π < α < 2 π

esetén

T' (α) < 0

.
Az utolsó előtti alakból viszont látjuk, hogy a derivált

cos \frac{α}{2} = 0

, azaz

α = π

esetén is értelmezve van és értéke

T' (π) = 0

. Csak itt lehet szélsőérték, és a derivált előjelére mondottak szerint itt szoros értelemben vett maximuma van

T (α)

-nak.
A szóban forgó terület tehát akkor a legnagyobb, ha az adott hosszúságot félkör alakúra hajlítjuk, és ekkor értéke

T = \frac{1}{2 π}