Kezdőlap


Feladat:	Pontversenyen kívüli P.132	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bartolits I. , Füredi Z. , Nagy S. , Neumann A. , Párkány Katalin , Stachó B.
Füzet:	1975/április, 158 - 160. oldal		PDF \| MathML
Témakör(ök):	Egyéb feladványok, Térbeli szimmetrikus alakzatok, Poliéderek szimmetriái, Térgeometriai bizonyítások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1972/február: Pontversenyen kívüli P.132

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szimmetriacentrummal bíró síkidom oldalainak száma páros, legegyszerűbb példája a paralelogramma, ilyenből 3-at véve egy közös csúcsba, már legalább 7 csúcsot adnak, ezért a föltevés szerinti poliéderek legegyszerűbb példája a paralelepipedon, és erre az állítás helyessége nyilvánvaló. (Két további példa lapunkból az 1407. gyakorlatban^{$^{*}$} vizsgált test és a rombdodekaéder^{$^{*}$}. Azt kell belátnunk, hogy a feltevés szerinti bármely $P$ poliéderhez található olyan $O$ pont, amelyre tükrözve $P$ -nek bármelyik lapját, a tükörkép ugyancsak lapja $P$ -nek.

1. Jelöljük

P

egy

L_{1}

lapja egyik ‐ függőlegesen tartott ‐ élének alsó végpontját

A_{1}

-gyel, a felsőt

B_{1}

-gyel, ezek tükörképét a lap szimmetriacentrumára

A_{2}

-vel, illetve

B_{2}

-vel. Ekkor a föltevést

L_{1}

-re alkalmazva,

A_{2} B_{2}

is éle

L_{1}

-nek, továbbá

A_{2} B_{2}

-ben csatlakozik

L_{1}

-hez

P

-nek egy további

L_{2}

lapja. Ennek szimmetria-középpontjára tükrözve

A_{2} B_{2}

-t, ismét egy

A_{3} B_{3}

élét kapjuk

P

-nek, rajta átléphetünk egy

L_{3}

lapra, és így tovább. Az

A_{1} B_{1}

A_{2} B_{2}

A_{3} B_{3}

...

élek egymással párhuzamosak, egyenlő hosszúak és a szomszédosak páronként ellentétes irányúak.
Ebben a tükrözési sorozatban eljutunk egy olyan

k

indexhez, amelyre az

A_{k + 1} B_{k + 1}

él ‐ amelyhez az

L_{k}

lap centrumán való tükrözéssel jutottunk, ‐ beleesik egy már megjelölt

A_{j} B_{j}

kép

(j < k)

egyenesébe, viszont az

A_{k} B_{k}

kép egyenese még minden korábbi kép egyenesétől különböző. Ha ugyanis nem volna ilyen

k

, akkor

P

-nek végtelen sok éle és lapja volna, amit pedig kizárhatunk. (Annak ellenére is kizárhatjuk ezt, hogy a kitűzés nem mondta ki; ezt az észrevételt a probléma az igényes megoldótól elvárja.) Ekkor

P

konvexsége alapján,

A_{k + 1}

vagy

A_{j}

-vel esik egybe, vagy

B_{j}

-vel, egyszersmind

B_{k + 1}

A_{j} B_{j}

él másik végpontjával, mert konvex testnek nem lehet két éle egymás meghosszabbításán; továbbá

j = 1

, mert

j > 1

esetén

A_{j} B_{j}

három lapnak,

L_{j - 1}

-nek,

L_{j}

-nek és

L_{k}

-nak lenne közös éle, ami ismét lehetetlen.
Az

L_{1}

L_{2}

...

L_{k}

lapok ‐ szögletes csődarabra emlékeztető ‐ együttesét a poliéder

A_{1} B_{1}

-gyel párhuzamos zónájának nevezzük (kristálytani kifejezéssel élve). Természetesen azt várjuk, hogy

L_{1}

-nek a várt

O

pontra való tükörképét az

L_{i}

lapok közt találjuk meg

(i = 3, ..., k - 1)

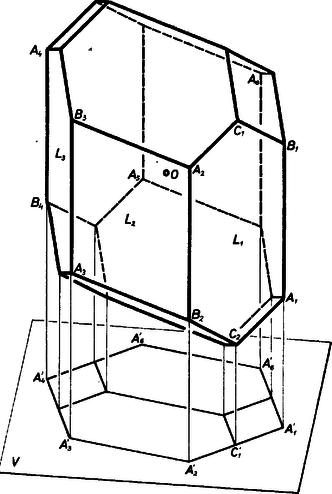
2. Vetítsük

P

-t

A_{1} B_{1}

irányú vetítéssel egy rá merőleges

V

(vízszintes) síkra és jelöljük bármely

X

alakzat (csúcs, lap) ilyen vetületét

X'

-vel. Így

A'_{i}

és

B'_{i}

egybeesik. Az

A'_{i} A'_{i + 1}

szakasz az

L_{i}

kerületéből annak a két résznek a közös vetülete, amelyekre az szétesik az

A_{i} B_{i}

és

A_{i + 1} B_{i + 1}

oldalak elhagyásával, hiszen

P

konvexsége alapján minden egyes lapja konvex sokszög, és

L_{i}

közte van a mondott párhuzamos éleknek.
Továbbá az

L_{i}

lap síkjának a vetülete az

A'_{i} A'_{i + 1}

egyenes, ezért

P

vetülete ennek az egyenesnek az egyik oldalára esik, hiszen

P

minden pontja az egyik oldalán van minden olyan síknak, amelyben benne van

P

-nek egy lapja. Ezt valamennyi

i

-re alkalmazva, az

A'_{1} A'_{2} ... A'_{k} = K

sokszög konvex, és

P

vetülete ennek a belsejébe és a kerületére esik; más szóval:

K

P

vetületének ún. kontúrvonala. Minden egyes

L_{i}

-t meghosszabbítva az

A_{i} B_{i}

és

A_{i + 1} B_{i + 1}

egyenesek közti végtelen síksávvá, e

k

síksáv együttese elhatárol egy végtelen hasábos térrészt, melynek alapidoma

K

és

P

benne van e térrészben.
A látott zóna

P

további lapjait szétválasztja két egymástól különálló részre, egy alsó

S_{a}

és egy felső

S_{f}

süvegre, pl.

S_{a}

-nak a zónával közös csúcsai

A_{1}

B_{2}

A_{3}

B_{4}

...

valamint az

L_{i}

lapok esetleges további csúcsai a mondottak szomszédos párjai között. A süvegek minden egyes lapjának

V

-n levő vetülete centrálszimmetrikus konvex sokszög, mert tükrös a lap centrumának vetületére, hiszen szakasz felezőpontjának vetülete felezi a szakasz vetületét. Egyetlen ilyen lap vetülete sem lehet egyenesszakasz, mert

P

-nek nincs további, az

A_{1} B_{1}

-gyel párhuzamos lapja. Az egy süvegbe tartozó lapok vetülete hézagtalanul és egyrétűen kitölti

K

-t, mert a hasábos tér belsejében,

A_{1} B_{1}

-gyel párhuzamosan haladó minden egyenes két pontban metszi

P

határfelületét, mindegyik süveget 1‐1 pontban. Ha tehát csak az egyik süveget vetítjük le,

K

-nak egy centrálszimmetrikus sokszögekre való felbontását kapjuk.
Alkalmazhatjuk erre a P. 144. probléma^{$^{*}$} megoldásában bizonyított állítást: ha egy konvex

K

sokszöget centrálszimmetrikus konvex sokszögekre lehet felbontani, akkor maga

K

is centrálszimmetrikus. Emiatt az

A_{1} B_{1}

éllel párhuzamos zónában páros sok él van,

k = 2 n

, tehát beszélhetünk szemközti élekről:

1 ≦ i ≦ n

mellett az

A_{i} B_{i}

éllel szemben az

A_{n + i} B_{n + i}

él van, két szomszédos él által meghatározott lap síkja párhuzamos a választott élekkel szemközti élek síkjával, és a szemközti élpárok távolsága egyenlő.

3. Az eddigiek szerint

P

tetszőleges

L

lapjának tetszőleges

A_{1} B_{1}

A_{2} B_{2}

élpárjához található

P

-nek olyan szemközti

L^{*}

lapja, amelyik párhuzamos

L

-lel, és amelyiknek van

A_{1} B_{1}

-gyel párhuzamos

A_{1}^{*} B_{1}^{*}

A_{2}^{*} B_{2}^{*}

élpárja, és még azt is tudjuk, hogy

A_{1} B_{1}

, és

A_{2} B_{2}

távolsága egyenlő

A_{1}^{*} B_{1}^{*} *

és

A_{2}^{*} B_{2}^{*}

távolságával. Alkalmazzuk ezt a megállapítást a

B_{1}

B_{2}

csúcsokhoz csatlakozó

B_{1} C_{1}

B_{2} C_{2}

élpárra (nem zárva ki az

A_{1} \equiv C_{2}

lehetőséget sem), kapjuk először is, hogy a párhuzamos lap csak

L^{*}

lehet, mert

P

-nek

L

-lel legfeljebb csak egy lapja lehet párhuzamos, és az

A_{1} B_{1}

A_{2} B_{2}

B_{1} C_{1}

B_{2} C_{2}

egyenesek által határolt paralelogramma egybevágó

L^{*}

megfelelő paralelogrammájával. Tehát

A_{1} A_{2}

és

A_{1}^{*} A_{2}^{*}

párhuzamosak és egyenlőek, és a felezőpontjaik által meghatározott szakasz felezőpontjára tükrözve őket egymásba mennek át. Feltehetjük, hogy

L^{*}

csúcsait eleve úgy betűztük meg, hogy ez a tükrözés

A_{1}

-t

A_{1}^{*}

-ba viszi. Az

A_{1} A_{2}

szakasz felezőpontja

L

szimmetriacentruma, tehát

A_{1} A_{1}^{*}

felezőpontja azonos az

L

és

L^{*}

szimmetriacentrumai által meghatározott szakasz felezőpontjával. Jelöljük ezt a felezőpontot

O

-val, mint láttuk,

O

helyzete nem függ attól, hogy

L

-en melyik csúcsot választjuk

A_{1}

szerepére, ami azt jelenti, hogy

L

-t

O

-ra tükrözve

L^{*}

-ot kapjuk.

4. Ezzel beláttuk, hogy

P

tetszőleges

L

lapjához található olyan

O

pont, amelyre

L

-t tükrözve ismét

P

valamelyik lapját kapjuk.

P

szomszédos lapjaihoz ugyanaz a centrum tartozik, hiszen e centrumot most már az az él meghatározza, amelyben a választott lapok egymáshoz csatlakoznak. Mivel bármely lapról bármely lapra eljuthatunk, szomszédos lapok láncolatán át,

P

tetszőleges lapjához ugyanaz az

O

centrum tartozik, vagyis

P

centrálszimmetrikus, amint azt bizonyítanunk kellett.

^{$^{*}$}Megoldását lásd K. M. L. 47 (1973) 62.

^{$^{*}$} Lásd pl. Csákány Bélának A méhek lépsejtjeiről, matematikus szemmel c. cikkében, K. M. L. 43 (1971) 109‐117. E cikkböl vettük ábránk ötletét Szerk.

^{$^{*}$}Megoldását lásd ezen szám 161. oldalán