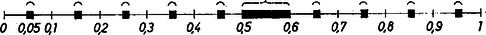Kezdőlap


Feladat:	Pontversenyen kívüli P.123	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bálint L. , Kollár J. , Kópházi J. , Reviczky J. , Szeredi J. , Szigeti G.
Füzet:	1974/február, 72 - 73. oldal		PDF \| MathML
Témakör(ök):	Tizes alapú számrendszer, Események algebrája, Geometriai valószínűség, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/december: Pontversenyen kívüli P.123

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A véletlenszerű kiválasztás a következőképpen értendő: annak valószínűsége, hogy a kiválasztott szám a $[0; 1]$ intervallum valamely $[a, b]$ vagy $[a, b)$ vagy $(a, b]$ vagy $(a, b)$ részintervallumába esik, egyenlő az intervallum $| b - a |$ hosszával.
Ha a kiválasztott szám tizedes tört alakjában az első $n$ jegy között előfordul 5-ös jegy, akkor a kiválasztott számot "jó szám''-nak fogjuk nevezni. Próbáljunk képet alkotni a jó számok elhelyezkedéséről. Ha $a_{1}$ , $a_{2}$ , $...$ , $a_{k}$ az 5-östől különböző számjegyek és $k ≦ n - 1$ , akkor a jobbról nyitott [ $0, a_{1} a_{2} ... a_{k} 5$ ; $0, a_{1} a_{2} ... a_{k} 6$ ) intervallum minden száma jó szám.
Fordítva, minden jó szám beletartozik egy, az előbbi típusú intervallumba, mert véve az első 5-ös jegyét ‐ legyen ennek a sorszáma $m$ , és legyenek ezt megelőző tizedes jegyei $a_{1}$ , $a_{2}$ , $...$ , $a_{m - 1}$ ‐, mindenesetre fennáll $m ≦ n$ és $a_{i} \neq 5$ , ha $i \leq m - 1$ , tehát a jó szám benne van a következő intervallumban:

\begin{matrix} [0, a_{1} a_{2} ... a_{m - 1} 5; 0,_{1} a_{2} ... a_{m - 1} 6) . \end{matrix}

(1)

Ábránk

n ≦ 2

-re szemlélteti a jó számokat tartalmazó intervallumokat.
Az (1) alakú intervallumok diszjunktok (páronként nincs közös pontjuk), ezért a keresett

P

valószínűséget az ilyen intervallumok hosszának összege adja meg. Az (1) hossza

10^{- m}

, az ilyenek száma annyi, ahányféleképp az

a_{1} a_{2} ... a_{m - 1}

szám megválasztható, vagyis

9^{m - 1}

, és együttes

9^{m - 1} \cdot 10^{- m}

hosszukat összegeznünk kell

m = 1

, 2,

...

n

-re.

\begin{matrix} P = \frac{1}{10} + \frac{9}{10^{2}} + \frac{9^{2}}{10^{3}} + ... + \frac{9^{n - 1}}{10^{n}} = \frac{1}{10} {1 + \frac{9}{10} + {(\frac{9}{10})}^{2} + ... + {(\frac{9}{10})}^{n - 1}} = 1 - {(\frac{9}{10})}^{n} . \end{matrix}

(1)-ből látható, hogy a tizedes törttel kétféleképpen előállítható számoknak a véges alakjára gondoltunk. Az első bekezdésben adott értelmezés szerint azonban nem változtat eredményünkön, ha a végtelen alakra gondolunk.

Megjegyzések. 1. A fenti megoldás a tankönyv egy "olvasmány'' jelzésű fejezetét használta fel.^{$^{*}$}
2. Ha

n \to \infty

, akkor

P \to 1

, eszerint annak valószínűsége, hogy a

[0; 1]

-ból véletlenszerűen kiválasztott szám tizedes tört alakjában szerepel 5-ös számjegy: 1 (biztos esemény). Ezt azonban már értelmezésünk tartalmazta.

II. megoldás. A kérdéses eseménnyel ellentétes esemény valószínűségét határozzuk meg.
Osszuk a

[0; 1]

intervallumot

10^{n}

számú, egymással egyenlő,

10^{- n}

hosszú részintervallumra, így az osztópontok azok a véges tizedes törtek, amelyeknek legföljebb

n

tizedes jegyük van, más szóval az 1, 2,

...

10^{n} - 1

egész számok

10^{- n}

-szeresei. Így minden egyes részintervallum minden száma akkor és csak akkor "nem jó'' szám, ha az intervallum bal végpontja nem jó szám.
A bal végpontok közül azok a nem jó számok, amelyeknek

10^{n}

-szeresében nem fordul elő az 5-ös, azaz minden jegyük a 0, 1, 2, 3, 4, 6, 7, 8, 9 közül való. Számuk

9^{n}

, így a nem jó intervallumok együttes hossza

{(\frac{9}{10})}^{n}

. Ebből értelmezhető az I. megoldás egyszerű eredménye.

^{$^{*}$} Czapáry E.‐Gyapjas F.‐Horvay Katalin‐Pálmay L.: Matematika a gimn. IV. o. számára, Tankönyvkiadó, Budapest, 1969. 269. oldal: Valószínűségek meghatározása geometriai módszerekkel.