Feladat:	Pontversenyen kívüli P.119	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balogh Zoltán ,  Hermann Péter ,  Nagy Sándor ,  Székely Albert ,  Totik V.
Füzet:	1975/január, 22 - 25. oldal		PDF  |  MathML
Témakör(ök):	Differenciálási szabályok, Trigonometrikus egyenlőtlenségek, Paraméteres egyenlőtlenségek, Határozatlan integrál, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/november: Pontversenyen kívüli P.119

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle \frac{1}{2}\left(\text{tg}x+\text{tg}nx-\text{tg}\left(n-1\right)x\right)>\frac{1}{n}\text{tg}nx\mathrm{.}}\end{array}$ (1) 1. Az $n=3$ esetben azt kell bizonyítanunk, hogy ha $0<x<\pi /6$, akkor $\begin{array}{c}{\displaystyle \frac{1}{2}\left(\text{tg}x+\text{tg}3x-\text{tg}2x\right)>\frac{1}{3}\text{tg}3x\mathrm{.}}\end{array}$ (2) A $\text{tg}x=y$ jelöléssel egyrészt $\begin{array}{c}{\displaystyle 0<y<\frac{1}{\sqrt[]{3}}\mathrm{,}}\end{array}$ (3) másrészt $\begin{array}{c}{\displaystyle \text{tg}2x=\frac{2y}{1-y^2}\mathrm{,}\text{tg}3x=\frac{3y-y^3}{1-3y^2}\mathrm{.}}\end{array}$ Ezeket (2)-be beírva, a bizonyítandó állítás ekvivalens átalakításokkal a következőbe megy át: $\begin{array}{c}{\displaystyle 3y+\frac{3y-y^3}{1-3y^2}>\frac{6y}{1-y^2}\mathrm{.}}\end{array}$ Itt a nevezők (3) szerint pozitívok, így újabb ekvivalens átalakításokkal $\begin{array}{c}{\displaystyle 3y\left(1-3y^2\right)\left(1-y^2\right)+y\left(3-y^2\right)\left(1-y^2\right)-6y\left(1-3y^2\right)=2y\left(1+5y^2\right)>0.}\end{array}$ Az utolsó alak helyessége nyilvánvaló, ezzel (2)-t bebizonyítottuk. Ha $nx$-et $a$-val jelöljük, és (1)-et a pozitív $\frac{x}{2}$-lel osztjuk, a $\begin{array}{c}{\displaystyle \frac{\text{tg}x-\text{tg}0}{x}+\frac{\text{tg}a-\text{tg}\left(a-x\right)}{x}>2\frac{\text{tg}a-\text{tg}0}{a}}\end{array}$ (4) egyenlőtlenséget kapjuk. Mi ezt fogjuk bizonyítani, és közben az $a$ és $x$ számokról csak azt használjuk fel, hogy $\begin{array}{c}{\displaystyle 0<x<\frac{a}{2}<\frac{\pi }{4}\mathrm{.}}\end{array}$ (5) Rögzített $a$ mellett a (4) bal oldalán álló kifejezés $x$ függvénye, jelöljük ezt a függvényt $f\left(x\right)$-szel. Ez a függvény az $x=\frac{a}{2}$ helyen egyenlő (4) jobb oldalával (1. ábra), így elég lesz belátni, hogy $f\left(x\right)$ monoton fogy a $0\le x\le \frac{a}{2}$ szakaszon. 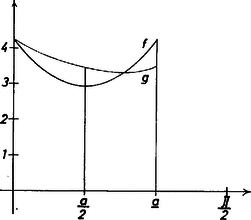    1. ábra   Mivel a $\text{tg}x$ függvény deriváltja $1/\text{cos}{}^{2}x$, a Newton-Leibniz formula szerint 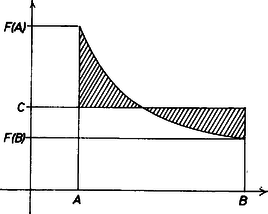${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{tg}x-\text{tg}0=\underset{0}{\overset{x}{\int }}\frac{dt}{\text{cos}{}^{2}t}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{tg}a-\text{tg}\left(a-x\right)=\underset{a-x}{\overset{a}{\int }}\frac{dt}{\text{cos}{}^{2}t}=\underset{0}{\overset{x}{\int }}\frac{dt}{\text{cos}{}^2\left(a-t\right)}\mathrm{.}}\hfill \end{array}}$ Emiatt $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{1}{x}\underset{0}{\overset{x}{\int }}\left[\frac{1}{\text{cos}{}^{2}t}+\frac{1}{\text{cos}{}^2\left(a-t\right)}\right]dt\mathrm{,}}\end{array}$ (6) azaz $f\left(x\right)$ a $\begin{array}{c}{\displaystyle g\left(t\right)=\frac{1}{\text{cos}{}^{2}t}+\frac{1}{\text{cos}{}^2\left(a-t\right)}}\end{array}$ (7) függvénynek ún. integrálközepe: $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{1}{x}\underset{0}{\overset{x}{\int }}g\left(t\right)dt\mathrm{.}}\end{array}$ (8)     2. ábra   Általában egy függvény integrálközepe egy szakaszon az a konstans, amivel a függvényt helyettesítve az integrálja nem változik meg: az $F\left(x\right)$ függvénynek az $\left(A\mathrm{,}B\right)$ szakaszon az integrálközepe $C$, ha (2. ábra) $\begin{array}{c}{\displaystyle \underset{A}{\overset{B}{\int }}F\left(x\right)dx=\underset{A}{\overset{B}{\int }}Cdx\mathrm{,}\text{azaz}C=\frac{1}{B-A}\underset{A}{\overset{B}{\int }}F\left(x\right)dx\mathrm{.}}\end{array}$ Ha $F\left(x\right)$ szigorúan monoton fogy az $A$, $B$ szakaszon, akkor $\begin{array}{c}{\displaystyle F\left(A\right)>\frac{1}{B-A}\underset{A}{\overset{B}{\int }}F\left(x\right)dx>F\left(B\right)\mathrm{,}}\end{array}$ (9) hiszen $F\left(x\right)$-et az egész $\left(A\mathrm{,}B\right)$ szakaszon $F\left(A\right)$-val helyettesítve az integrál nő, $F\left(B\right)$-vel helyettesítve pedig fogy: $\begin{array}{c}{\displaystyle \underset{A}{\overset{B}{\int }}F\left(A\right)dx<\underset{A}{\overset{B}{\int }}F\left(x\right)dx<\underset{A}{\overset{B}{\int }}F\left(B\right)dx\mathrm{.}}\end{array}$ Ennek alapján azt várjuk, hogy ha a $g\left(x\right)$ függvény monoton fogy a $0\le x\le b$ szakaszon, akkor a $\left(\mathrm{0,}x\right)$ szakaszon vett integrálközepe az $x$ monoton fogyó függvénye. Valóban, ha $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{1}{x}\underset{0}{\overset{x}{\int }}g\left(t\right)dt\mathrm{,}}\end{array}$ és $0<x<y\le b$, akkor $f\left(x\right)<g\left(x\right)$, és ${\displaystyle \begin{array}{c}\hfill {\displaystyle \underset{0}{\overset{y}{\int }}g\left(t\right)dt=\underset{0}{\overset{x}{\int }}g\left(t\right)dt+\underset{x}{\overset{y}{\int }}g\left(t\right)dt=\underset{0}{\overset{x}{\int }}f\left(x\right)dt+\underset{x}{\overset{y}{\int }}g\left(t\right)dt<\underset{0}{\overset{x}{\int }}f\left(x\right)dt+\underset{x}{\overset{y}{\int }}f\left(x\right)dt=\underset{0}{\overset{y}{\int }}f\left(x\right)dt\mathrm{,}}\hfill \end{array}}$ tehát az $f\left(x\right)$ konstansokkal a $\left(\mathrm{0,}y\right)$ szakaszon vett integrálja nagyobb $g$ integráljánál, és így $g$ integrálközepe kisebb $f\left(x\right)$-nél: $\begin{array}{c}{\displaystyle \frac{1}{y}\underset{0}{\overset{y}{\int }}g\left(t\right)dt<\frac{1}{y}\underset{0}{\overset{y}{\int }}f\left(x\right)dt=f\left(x\right)\mathrm{.}}\end{array}$ Ha tehát belátjuk, hogy a (7) alatti $g\left(t\right)$ függvény monoton fogy a $0\le t\le \frac{a}{2}$ szakaszon, akkor ebből következik, hogy ott a (8)-cal definiált $f\left(x\right)$ függvény is monoton fogy, és azt már beláttuk, hogy ebből következik (4). A $g\left(t\right)$ függvény deriváltja, $\begin{array}{c}{\displaystyle g\text{'}\left(t\right)=\frac{2\text{tg}t}{\text{cos}{}^{2}t}-\frac{2\text{tg}\left(a-t\right)}{\text{cos}{}^2\left(a-t\right)}}\end{array}$ $0<t<\frac{a}{2}$ mellett negatív, mert $0<t<a-t<\frac{\pi }{2}$ miatt $\begin{array}{c}{\displaystyle 0<\text{tg}t<\text{tg}\left(a-t\right)\text{és}0<\text{cos}\left(a-t\right)<\text{cos}t\mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle \frac{\text{tg}t}{\text{cos}{}^{2}t}<\frac{\text{tg}\left(a-t\right)}{\text{cos}{}^2\left(a-t\right)}\mathrm{,}}\end{array}$ állításunkat ezzel bebizonyítottuk.