Feladat: Pontversenyen kívüli P.118 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Reviczky János ,  Totik Vilmos ,  Turán György 
Füzet: 1972/október, 72 - 77. oldal  PDF  |  MathML 
Témakör(ök): Trigonometrikus egyenletrendszerek, Paraméteres egyenletrendszerek, Függvények, Függvény határértéke, Mértani helyek, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1971/november: Pontversenyen kívüli P.118

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a=sin2x,b=cos2y, ekkor

0≤a≤1;0≤b≤1,(4)
teljesül tetszőleges x, y mellett, és könnyen látható az is, hogy ha a, b olyan számpár, amelyre (4) teljesül, akkor van olyan x, y számpár, amelyre sin2x=a, cos2y=b. Emiatt feladatunk ekvivalens a következővel: határozzuk meg a sík azon P(u,v) pontjainak mértani helyét, melyekre az
f(a)+f(b)=u,(5)a+b=v(6)


egyenletrendszernek van olyan a,b megoldása, amelyre (4) teljesül. (4)-ből és (6)-ból azonnal látható, hogy
0≤v≤2,(i)
ez az (u,v) számpárra vonatkozó első szükséges feltétel.
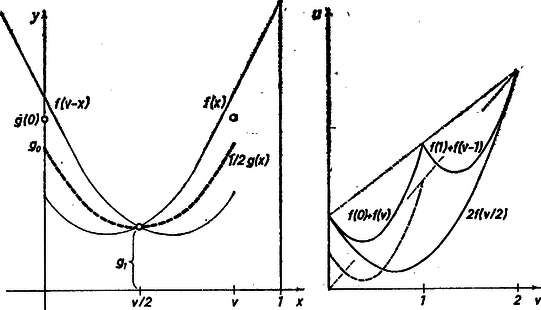
Legyen először v a zárt [0,1] intervallum tetszőleges rögzített pontja: 0≤v≤1. Ekkor u a
g(x)=f(x)+f(v-x)(7)
függvény értékkészletét futja be, ha a függvényt azokra az x-ekre értelmezzük, amelyekre az
a=x,b=v-x
számokra teljesül (4), tehát amelyekre
0≤x≤1,0≤v-x≤1,
azaz 0≤x≤v.
A v=0 esettől mint triviálistól a továbbiakban eltekintünk, hiszen ekkor g értékkészlete a g(0)=2f(0) számból áll. Legyen tehát 0<v≤1, ekkor g értelmezési tartománya a zárt [0,v] intervallum. Itt ez a függvény szimmetrikus az x=v2 abszcisszájú pontra:
g(v2+Δ)=f(v2+Δ)+f(v2-Δ)=g(v2-Δ),
tehát g-nek a [0,v] feletti értékkészlete megegyezik a [0,v2] feletti értékkészletével. Megmutatjuk, hogy g az egész [0,v] intervallumban konvex, és [0,v2]-ben monoton fogy, [v2,v]-ben monoton nő. Valóban, legyen 0≤x1<x2≤v és legyen λ a [0,1] intervallum tetszőleges pontja, akkor
g(λx1+μx2)=f(λx1+μx2)+f(λy1+μy2)≤≤λ[f(x1)+f(y1)]+μ[f(x2)+f(y2)]=λg(x1)+μg(x2),


ahol μ=1-λ, y1=v-x1, y2=v-x2. Ezzel beláttuk, hogy g konvex, és rátérünk annak a bizonyítására, hogy a [0,v2] szakaszon monoton fogy.
A konvexség definíciójában szereplő
xλ=λx1+(1-λ)x2
abszcisszájú, és
yλ=λf(x1)+(1-λ)⋅f(x2)
ordinátájú Hλ(xλ, yλ) pont az (x1,f(x1)), (x2,f(x2)) pontokat összekötő szakasz pontja, nevezetesen az a pont, amely a szakaszt (1-λ):λ arányban osztja. Jelöljük e(x;x1,x2)-vel azt a lineáris függvényt, amelynek az értéke x1-ben f(x1), x2-ben f(x2). A Hλ pont rajta van ennek a függvénynek a képén, így a konvexség feltétele azt jelenti, hogy az x1≤x≤x2 szakaszon az f(x) függvény képe e(x;x1,x2) alatt halad:
f(x)≤e(x;x1,x2),hax1≤x≤x2.

Szükségünk lesz arra is, hogy ha f(x) konvex, akkor
f(x)≥e(x;x1,x2),hax<x1,vagyx>x2.
Valóban, legyen például x0<x1, akkor f(x) konvex volta miatt
f(x1)≤e(x1;x0,x2),
viszont f(x1)=e(x1;x1,x2), tehát az e(x;x1,x2) lineáris függvény x<x2 mellett e(x;x0,x2) alatt halad:
f(x0)=e(x0;x0,x2)≥e(x0;x1,x2).
E megjegyzés után visszatérünk g monotonitásának a bizonyítására.
Legyen y1 és y2 az f(x) értelmezési tartományának oly pontja, melyre y1≤x1, y2≥x2 teljesül, azaz legyen az [x1,x2] szakasz az [y1,y2] szakasz része. Mivel f(x) az e(x;y1,y2) alatt van, azért e(x;y1,y2) alatt van f(x)-nek az e(x;x1,x2) húrja is. Valóban, ha x1≤x≤x2, akkor
e(x;x1,x2)=x2-xx2-x1f(x1)+x-x1x2-x1f(x2)≤≤x2-xx2-x1e(x1;y1,y2)+x-x1x2-x1e(x2;y1,y2)=e(x;y1,y2).


Ennek speciális eseteként kapjuk, hogy ha 0≤y1<x1≤v2, akkor
g(y1)=f(y1)+f(y2)=2e(v2;y1,y2)≥2e(v2;x1,x2)=f(x1)+f(x2)=g(x1),
ahol y2=v-y1, x2=v-x1. Tehát g valóban monoton fogyó a [0,v2] szakaszon.
A g függvény ‐ mint minden konvex függvény ‐ folytonos az értelmezési tartományának minden belső pontjában. Legyen ugyanis f(x) a p≤x≤q szakaszon konvex, és legyen p<x0<q. Akkor p≤x≤x0, mellett
e(x;x0,q)≤f(x)≤e(x;p,x0),
ha pedig x0≤x≤q, akkor
e(x;p,x0)≤f(x)≤e(x;x0,q).
 

 


Eszerint
min{e(x;p,x0),e(x;x0,q)}≤f(x)≤max{e(x;p,x0),e(x;x0,q)}.
Mivel ennek az egyenlőtlenség láncnak a két szélén folytonos függvények állnak, és ezeknek az x=x0 helyen felvett értéke egyenlő, f(x) is folytonos x0-ban.
Könnyen látható, hogy ha f(x) konvex [p,q]-ban, akkor f-nek a p-beli értékét tetszőleges, f(p)-nél nagyobb számmal helyettesítve ismét konvex függvényt kapunk. Emiatt a [p,q]-ban konvex f függvény a végpontokban nem feltétlenül folytonos. Így van ez a fenti g függvény esetében is, ezért nem várható, hogy a [0,v2]-ben monoton g függvény értékkészlete az egész [g(v2),g(0)] szakasz legyen. Mivel g monoton, létezik az x=0 pontban a jobb oldali határértéke, jelöljük ezt g0-lal. Megmutatjuk, hogy g értékkészlete az
u=g(0)=f(0)+f(v)(ii)
számból, és a
g1≤u<g0(iii)
számokból áll, ahol
g0=limx→0x>0[f(x)+f(v-x)]ésg1=g(v2)=2f(v2).
(Ha a g0 határérték egyenlő a g1 függvényértékkel, akkor g értékkészlete a g(0) és a g1 számokból áll.)
Ennek érdekében ‐ többek között ‐ azt kell megmutatnunk,
hogy ha u0 tetszőleges valós szám, melyre g1≤u0<g0 teljesül, akkor van olyan 0<x0≤v2 amelyre g(x0)=u0. Legyen A azoknak az x valós számoknak a halmaza, amelyekre
0<x≤v2ésg(x)<u0
teljesül. Mivel g monoton fogy és g0>u0, azért az x=0 hely alkalmas környezete A-hoz tartozik, és ha x∈A, akkor az egész (0,x) szakasz A-hoz tartozik. Emiatt A maga is egy intervallum, jelöljük x0-lal A jobb oldali végpontját (x0 az A-beli számok felső határa: a legkisebb olyan szám, amelynél A egyetlen eleme sem nagyobb). Akkor 0<x0≤v2<v miatt g folytonos x0-ban, tehát x0-beli értéke egyenlő itteni határértékével. Ez csak u0 lehet, hiszen A definíciója szerint g-nek x0-beli bal oldali határértéke legalább u0, ha pedig g(x0)>u0 volna, x0-nak valamely alkalmas környezete teljes egészében A-hoz tartozna. Tehát a balról zárt, jobbról nyílt [g1,g0] intervallum (a g1=g0 esetben a g1 pont) g értékkészletéhez tartozik. Nyilván oda tartozik a g(0) érték is, így már csak azt kell belátnunk, hogy más érték nem tartozik g értékkészletéhez. Mivel g monoton, e számokon kívül csak g0 tartozhatna még g értékkészletéhez. Ha azonban van olyan 0<x0≤v2, melyre g(x0)=g0, akkor g monoton és konvex volta miatt g(x)=g0, volna minden 0<x≤v2 mellett, tehát g0 csak akkor tartozhat g értékkészletéhez, ha egyenlő g1-gyel.
Ezzel beláttuk, hogy ha 0≤v≤1, akkor a keresett P(u,v) pontok azok és csakis azok, amelyeknek első koordinátájára (ii) vagy (iii) teljesül. Hasonlóan kapjuk, hogy ha 1≤v≤2, akkor az
u=g(1)=f(1)+f(v-1)
szám és a
g1≤u<g2
balról zárt, jobbról nyílt szakasz a keresett P(u,v) pontok első koordinátájának a mértani helye, ahol
g2=limx→1x<1[f(x)+f(v-x)].
Ezzel a kérdésre megadtuk a választ. A keresett mértani helyet az (i), (ii) és (iii) feltételek írják le.
 

Megjegyzések. 1. Megkaphatjuk a keresett (v,u) számpárokat úgy is, hogy vesszük a (v,u) síkon az u=2f(v2) függvény összes húrjának a felezőpontját ‐ pontosabban: e felezőpontok koordinátáit. Ha f folytonos a [0,1] szakasz végpontjaiban, akkor a keresett mértani hely a (v,u) síkon a h1(v)=2f(v2) és a
h2(v)={f(0)+f(v)ha0≤v≤1,f(1)+f(v-1)ha1<v≤2
függvények képei által határolt idom.
 

2. Többször használtuk a következő állítást: ha az an, sorozat monoton nő és felülről korlátos, akkor konvergens. Legegyszerűbb, ha azt mondjuk, ez a valós számoknak alaptulajdonsága, és ezért nem kell bizonyítanunk. Mint a geometriában, a matematika más területein is axiómákkal, alaptulajdonságokkal definiálhatjuk az alapfogalmakat. Így a valós számokat is úgy definiálhatjuk, hogy felsoroljuk mindazokat a tulajdonságokat, amelyek a valós számokat alapvetően jellemzik. Az alapműveletekkel kapcsolatos tulajdonságokon kívül két tulajdonságot szokás még axiómának tekinteni: az egyik azt biztosítja, hogy beszélhessünk "akármilyen nagy'' valós számról, a másik pedig azt, hogy a valós számok összességében "ne legyen lyuk''. Az utóbbi tulajdonságnak az egyik lehetséges változata a megoldásunkban használt állítás.