Kezdőlap


Feladat:	Pontversenyen kívüli P.116	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balogh Zoltán , Breuer Péter , Császár Gyula , Oláh Vera
Füzet:	1972/május, 216 - 218. oldal		PDF \| MathML
Témakör(ök):	Ellipszis egyenlete, Hiperbola egyenlete, Ellipszis, mint mértani hely, Hiperbola, mint mértani hely, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/október: Pontversenyen kívüli P.116

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatot a koordináta-geometria eljárásával oldjuk meg. Legyen a két tengely az $e_{1}$ , $e_{2}$ egyenespár közép párhuzamosa, illetőleg az $f$ egyenes, legyen $e_{1}$ egyenlete $y = g$ $(> 0)$ , ekkor $e_{2}$ egyenlete $y = - g$ . A koordináta-rendszer használata könnyűvé teszi annak tekintetbevételét, hogy $P_{1}$ és $P_{2}$ az $f$ -nek ugyanazon az oldalán vannak-e, vagy ellentétes oldalán. Ugyanis $O_{i} P_{i}$ -t $(i = 1,2)$ előjellel ellátva ‐ vagyis helyette $P_{i}$ abszcisszáját írva ‐, $P_{1}$ és $P_{2}$ akkor és csak akkor vannak $f$ ugyanazon (ill. ellentétes) oldalán, ha a két abszcissza szorzata pozitív (ill. ha negatív). Eszerint a feladat két kérdésének elindítását egybe is foglalhatjuk így: $O_{1} P_{1} \cdot O_{2} P_{2} = k$ legyen, ahol az eredeti kérdésben $k = 1$ , a kiegészítő kérdésben 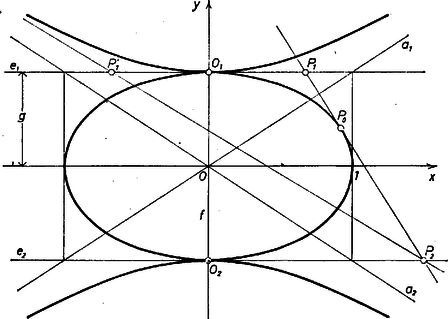$k = - 1$ .

Előre látjuk, hogy ha a sík egy

P (x, y)

pontján át rajzolható egy megfelelő

P_{1} P_{2}

egyenes, akkor ennek az egyenesnek minden pontja megfelel

P

szerepére.
Az is világos, hogy az

e_{1}

és

e_{2}

egyeneseknek ‐

O_{1}

, ill.

O_{2}

kivételével ‐ minden pontja hozzátartozik a mértani helyhez, mert ha

e_{1}

-nek egy

O_{1}

-től különböző pontja

P

, akkor

e_{2}

-nek

f

-től, azaz

O_{2}

-től

1 / O_{1} P

távolságra levő pontjai

P

-vel együtt megfelelő pontpárt alkotnak, éspedig a

P

-vel egyező oldalon levő

P'

az eredeti kérdés szempontjából, az

f

túlsó oldalán levő pedig a kiegészítő kérdés szempontjából. Maga

O_{1}

viszont nyilvánvalóan nem felelhet meg, sem az

O_{2}

pont.
Mármost az az állítás (föltevés), hogy

P

hozzátartozik a keresett mértani helyhez, azt jelenti, hogy tartozik hozzá olyan

p (\neq 0)

szám, amellyel és

P_{1} (p, g)

és

P_{2} (k / p, - g)

az előírásnak megfelelő pontok, tehát

P (x, y)

rajta van a

P_{1} P_{2}

egyenesen, koordinátái kielégítik ennek egyenletét, azaz teljesül

\begin{matrix} - 2 g (x - p) = (\frac{k}{p} - p) (y - g), \end{matrix}

(1)

átrendezve

\begin{matrix} (y + g) p^{2} - (2 g x) p - k (y - g) = 0 \end{matrix}

(2)

Miután fenti megjegyzésünkkel az

e_{1}

-beli

P (x, g)

és

e_{2}

-beli

P (x, - g)

pontokat már megvizsgáltuk a mértani hely szempontjából, elég tekintenünk az

| y | \neq g

ordinátájú pontokat. Így (1) a

p

-re mint ismeretlenre vonatkozóan valódi másodfokú egyenlet, és egyik gyöke sem

0

P

fent mondott létezését természetesen úgy értjük, hogy a hozzá tartozó

p

valós, tehát (2) diszkriminánsa nem negatív, azaz teljesül:

\begin{matrix} {(2 g x)}^{2} + 4 k (y^{2} - g^{2}) ≧ 0. \end{matrix}

(3)

Innen

4 g^{2} k

-val osztva és kellően rendezve,

k > 0

, azaz

k = 1

esetében

\begin{matrix} x^{2} + \frac{y^{2}}{g^{2}} - 1 ≧ 0, azaz \frac{y^{2}}{g^{2}} ≧ 1 - x^{2}, \end{matrix}

(4)

k < 0

, azaz

k = - 1

esetén pedig

\begin{matrix} - x^{2} + \frac{y^{2}}{g^{2}} - 1 ≦ 0, azaz \frac{y^{2}}{g^{2}} ≦ 1 + x^{2} . \end{matrix}

(5)

Ezek szerint az eredeti kérdésben (4), a kiegészítő kérdésben (5) a szükséges feltétele annak, hogy a

P (x, y)

pont ‐ ahol

| y | \neq g

‐ hozzátartozzék a mértani helyhez.
(4)-ben az egyenlőség annak az ellipszisnek a pontjaira teljesül, melynek szimmetriatengelyei azonosak a koordinátatengelyekkel, az

x

tengelyen fekvő szimmetriatengely fele-hossza

1

, a másiknak a fele-hossza

g

. Az utóbbi tengely végpontjai tehát

O_{1}

és

O_{2}

, ezeket már fentebb kizártuk. (Ha

g = 1

, akkor körről van szó.) Az egyenlőtlenség jelével pedig az ellipszisre (körre) nézve külső pontok teljesítik (4)-et, amelyekre nézve az ordináta abszolút értéke nagyobb, mint az ugyanazon abszcisszán levő ellipszispont ordinátájának abszolút értéke, ill.

x > 1

esetén minden

y

.
(5)-ben az egyenlőség annak a hiperbolának a pontjaira teljesül, melynek képzetes tengelye az

x

tengely, a tengely fele-hossza

1

(a szokásos jelölés szerinti

b

), valós (a fókuszokat tartalmazó) tengelye az

y

tengely, az utóbbinak a fele-hossza

g

(a szokásos jelölés szerinti

a

), tehát a hiperbola csúcsai

O_{1}

és

O_{2}

(ezeket már kizártuk), fókuszainak ordinátái

\pm \sqrt[]{g^{2} + 1}

. Az egyenlőtlenség jelével viszont a hiperbolára nézve külső pontok teljesítik (5)-öt, más szóval a két ág közti, az

x

tengely felé eső pontok, a fókuszokat nem tartalmazó síkrész pontjai. A hiperbola aszimptotái egyszersmind annak a téglalapnak az átló egyenesei, amelynek oldalegyenesei a (4) ellipszishez a tengelyvégpontokban húzott érintők.
Fordítva, ha valamely

P (x, y)

pontra teljesül (3), és

| y | \neq g

, akkor a (2) egyenletnek van

0

-tól különböző valós gyöke, jelöljük ezt

p

-vel. Erre a

p

-re teljesül (1) is, ami éppen azt jelenti, hogy a

P_{1} (p, g)

és

P (x, y)

pontokon átmenő egyenes átmegy a

P_{2} (k / p, - g)

ponton is, tehát ez az egyenes megfelel a feladat követelményeinek. Ha tehát

| y | \neq g

úgy (3) a szükséges és elégséges feltétele annak, hogy a

P

pont a vizsgált mértani helyhez tartozzék.
Meg lehet mutatni, hogy ha

P_{0}

rajta van az ellipszisen, ill. hiperbolán (és

P_{0} \neq O_{1}

O_{2}

), akkor a (2)-ből kapott egyetlen

p

érték az ellipszis (hiperbola)

P_{0}

-beli érintőjét határozza meg; ha pedig

P_{0}

külső pont, akkor a kapott két

p

érték a kúpszelet

P_{0}

-on átmenő két érintőjét adja ‐ természetesen az (1)-be való behelyettesítéssel.
Végül a koordinátarendszertől függetlenül így mondható ki eredményünk. Tekintsük azt az ellipszist, melynek egyik tengelye az

O_{1} O_{2}

szakasz (ill. azt a hiperbolát, melynek valós tengelye az

O_{1} O_{2}

szakasz), a másik tengelyének hossza pedig

2

egységnyi hosszú. A keresett mértani helyet mindazok a pontok alkotják, amelyeken át lehet érintőt fektetni az ellipszishez (hiperbolához), kivéve közülük az

O_{1}

O_{2}

pontokat.