|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Először egy tételt idézünk és bizonyítunk. Ha adott a síkban pont (), melyek nincsenek mind egy egyenesen, akkor van olyan egyenes, mely pontosan kettőn megy át az adott pontok közül. Legyenek az adott pontok , , , .
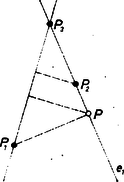
Tekintsük azokat az egyeneseket, amelyeken legalább kettő van rajta az adott pontok közül,így nyerjük az , , egyeneseket, . Tekintsük minden egyes távolságát minden egyes olyan -től, mely nem megy át -n. Válasszuk úgy a pontok és az egyenesek indexeit, hogy e távolságok közt ne forduljon elő kisebb, mint távolsága -től. Azt állítjuk, hogy ekkor -en pontosan kettő van az adott pontok közül.
Jelöljük a -ből -re bocsátott merőleges talppontját -vel. Ha -en legalább 3 pontunk van, akkor közülük kettő van a -nek valamelyik oldalán, legyenek ezek és úgy, hogy legyen ( esetleg egybe is eshet -vel). A háromszögben , vagyis ebben a háromszögben a -hoz tartozó magasság kisebb a -hoz tartozó magasságnál, közelebb van a egyeneshez, mint az -hez. Ellentmondásra jutottunk, így -en csak kettő lehet az adott pontok közül ‐ annyi viszont van is.
Gallai tételét a következő átfogalmazásban fogjuk felhasználni: ha adott a síkban különböző pont úgy, hogy bármelyik kettőjük összekötő egyenesén van legalább egy további az adott pontok közül, akkor ez az pont egyetlen egyenesen helyezkedik el (hiszen csak így lehetséges, hogy ne legyen olyan összekötő egyenesük, mely pontosan kettőn megy át a pontok közül).
2. Rátérve feladatunkra, csak esetére kell bizonyítanunk az állítást, hiszen esetében még nincs mit bizonyítani. Legyenek a pontjaink , , , és , és vegyünk egy olyan síkot, amely nem megy át -n és nem párhuzamos a (, 2 , ) egyenesek egyikével sem. (Létezik ilyen sík, hiszen véges számú egyenesről van szó.) Legyen a egyenesnek -sel való metszéspontja , ez db különböző pont, mert egyetlen egyenes sem megy át valamely másik ponton. Segédtételünk alapján azt mutatjuk meg, hogy a pontok egyetlen egyenesen vannak ; ebből már következik, hogy mind az pontunk a síkban van benne.
Vegyük -t és még kettőt a további pontjaink közül, mondjuk -et és -t. Az egyértelműen meghatározott síkban a föltevés szerint legalább egy további pontunk is van, legyen egy ilyen a . Ekkor , , egy egyenesen van, a síknak -sel való metszésvonalán. Ugyanígy bármely , , ponthármas egy egyenesen van, ahol és rajta van a síkon.
Ezek szerint a különböző pontokból álló pontrendszer (, 2, , ) egy síkban van és eleget tesz az átfogalmazott Gallai‐tétel föltételeinek, tehát valóban egyetlen egyenesen helyezkednek el.
Megjegyzés. A föltevés első részéből csak azt használtuk ki, hogy van olyan az adott pontok közt ‐ ti. olyan ‐, amelyen a többiek közül vett semelyik kettőnek az összekötő egyenese nem megy át. Kár lenne azonban a föltétel szépen, egyszerűen kimondott állítását elkomplikálni ; az ilyesmi általában sem szokásos.
Ha azonban a föltevés első részét úgy módosítanók, hogy minden pontunkon menne át más kettőnek összekötő egyenese úgy, hogy pontjaink 2 egyenesre lennének felfűzve, mindegyik egyenesre legalább 3 pont, és e 2 egyenes kitérő lenne egymáshoz képest, akkor az állítás már nem lenne igaz.
Érkezett 15 dolgozat, de egyik sem megoldása a problémának.
Jutalmul 100‐100 Ft értékű könyvutalványt kapott pontversenyen kívül : Bálint László, Balogh Zoltán, Reviczky János és Stachó Balázs.
Gallai Tibor tétele, lásd következő cikkünkben: Erdős Pál: Néhány elemi geometriai problémáról, K.M.L. 24 (1962) 193‐201. |
 PDF |
PDF |  MathML
MathML