| Feladat: | Pontversenyen kívüli P.110 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Füzet: | 1975/április, 157 - 158. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyenlőtlenségek, Határozatlan integrál, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1971/szeptember: Pontversenyen kívüli P.110 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. a) Az integrálszámítás egyik nevezetes egyenlőtlensége szerint ha az , függvényeknek a négyzete is integrálható, akkor
b) Feltevésünk szerint alulról konkáv, azaz felülről konvex. Mivel , ez az utóbbi azt jelenti, hogy a koordinátasíknak az tengely és az képe által közrefogott része konvex halmaz. Tekintsük ennek a halmaznak a vízszintes húrjait, és rendeljük hozzá mindegyikhez azt a háromszöget, amelyiknek az alapja az tengely 0 és 1 pontjai közötti szakasza, és a szárai átmennek a húr végpontjain. Jelöljük az magassághoz tartozó húr esetében ezt a háromszöget -mel, -nek által le nem fedett részének a területét -mel és -nek által le nem fedett részét -mel. Mivel konvex, ha , tartalmazza -t, és , . Az magasság legnagyobb szóbajöhető értéke egyenlő maximumával, -mel. nyilván , és mivel területe kisebb területénél, . Az -re szóbajöhető legkisebb érték az , számok kisebbike, pontosabban mondva ez az érték már választható -nek. Itt határértéke 0, és mint az könnyen látható, az , függvények folytonosak. Tehát van olyan , amelyre 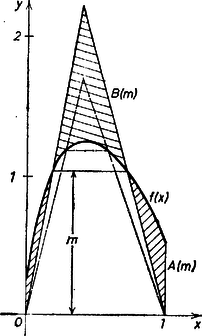 mert |