Feladat: Pontversenyen kívüli P.108 Korcsoport: - Nehézségi fok: nehéz
Megoldó(k):  Császár Gyula ,  Major Imre ,  Totik Vilmos 
Füzet: 1973/február, 71 - 73. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Vetítések, Háromszögek nevezetes tételei, Simson-egyenes, Körülírt kör, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1971/május: Pontversenyen kívüli P.108

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az állítást annak megmutatásával bizonyítjuk, hogy a két háromszög megfelelő oldalegyenespárjait egymással egyenlő nagyságú, ellentétes irányú elfordulások viszik át egymásba. Pontosabban: az A', B', C' ponthoz megszerkesztett Simson-egyenest rendre sa-val, sb-vel, sc-vel jelölve, az AB,BC,CA egyenest pedig rendre c-vel, a-val, b-vel, az sa-t sb-be átvivő elfordulás, valamint az a-t b-be vivő elfordulás egyenlők, de ellentétes irányúak s i. t. (1. ábra).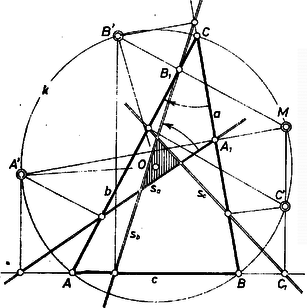

 

 

1. ábra
 

Evégett megvizsgáljuk, hogyan változik M-nek k-n való elmozdulása hatására a hozzá tartozó sM Simson-egyenes iránya. Megmutatjuk előkészítésül, hogy az AA', BB' és CC' egyenesek mindegyike párhuzamos sM-mel (2. áb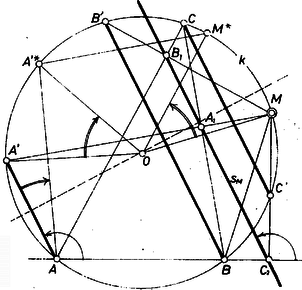ra).
 

 

2. ábra
 

Valóban, a k-ban, valamint az MA, MB, MC átmérők fölötti Thalész-körökben keletkezett húrnégyszögek alapján
BAA'∢=180∘-BMA1∢=180∘-BC1A1∢,ABB'∢=AMB1∢=AC1B1∢,ACC'∢=AMC1∢=AB1C1∢,


és ezek igazolják utóbbi állításunkat. (Az A, B, C és M pontok kölcsönös helyzete szerint e bizonyítás csekély ‐ nem lényeges ‐ módosulásokat mutathat; ha pedig pl. A' egybeesik A-val, akkor az AA' egyenes helyett k-nak A-beli érintője értendő.)
Forduljon el mármost az OM sugár OM*-ba. Ekkor A'-nek új, A'* helyzetét az M*-on át MA'-vel párhuzamos egyenes metszi ki, így MM* és A'A'* egyenlő és ellentétes irányú ívei a k-nak, és az M*-hoz tartozó Simson-egyenes AA'* iránya sM-éhez képest
A'AA'*∢=12A'OA'*∢=-12MOM*∢
-gel van elfordulva, ahol a mínusz jel arra utal, hogy az elfordulás iránya ellen-tétes az OM-et OM*-ba átvivő elfordulás irányával.
M szerepére A'-t, M* szerepére B'-t helyettesítve, ennek alapján azt kapjuk, hogy sb az sa-hoz képest (-1/2)A'OB'∢-gel van elfordulva (1. ábra). Ez pedig egyenlő a (+1/2)AOB forgásszöggel, hiszen az előbbiek szerint az A'B'C' háromszög úgy áll elő ABC-ből, hogy ezt tükrözzük k-nak sM-re merőleges átmérőjére mint tengelyre. Végül az már nyilvánvaló, hogy (1/2)AOB∢=-BCA∢, és ez az a-t b-be vivő elfordulás negatívja.
A betűzés kellő megváltoztatásával meggondolásunk az (sb,sc)∢=-(b,c)∢ egyenlőséget adja; ezzel az állítást bebizonyítottuk.
 

Megjegyezzük végül: előfordulhat, hogy az A', B', C' pontokhoz tartozó Simson-egyenesek nem alkotnak háromszöget, mindhárom egy ponton megy át. Ilyen helyzet adódik, ha a kiindulási A, B, M, C pontok egy húrdeltoid csúcsai és AM a szimmetriatengely.
 

II. megoldás. 1. Ismeretes, hogy az ABC háromszög K magasságpontjának a BC, CA, AB egyenesekre vonatkozó A*,B*,C* tükörképe rajta van az ABC köré írható k körön, tehát az A*M,B*M,C*M egyeneseknek a BC, CA, AB egyenesekre vonatkozó tükörképe átmegy K-n (3. ábra). Ha belátjuk, hogy ezeknek a tükörképeknek az állása megegyezik, kapjuk, hogy M-nek a BC, CA, AB egyenesekre vonatkozó tükörképei: M'BC, M'CA, M'AB egy egyenesen vannak. Mivel a tükörképeket az M centrumú, 1/2 arányú hasonlóság M-nek az ABC oldalaira eső vetületeibe viszi, ezzel egyrészt bebizonyítjuk a Simson-egyenes létezését, másrészt meghatározzuk ennek az egyenesnek az állását.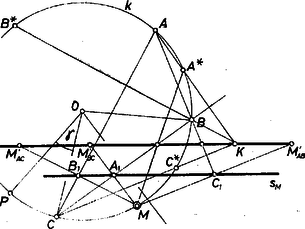
 

 

3. ábra
 

2. Válasszuk a k kör O középpontját origónak, és k valamelyik OP sugarát alapul véve jellemezzük k pontjait azzal a forgásszöggel, amekkora forgatás OP-t az illető ponthoz tartozó sugárba viszi; a sík egyeneseinek az állását pedig jellemezzük k valamelyik velük párhuzamos sugarának a forgśszögével. ‐ Jelöljük az A, B, C, M pontokhoz tartozó forgásszögeket α-val, β-val, γ-val és μ-vel. A BOC szög felezőjének az állása jellemezhető az 12(β+γ) forgásszöggel, a rá merőleges BC egyenes állása pedig az 12(β+γ+π) forgásszöggel. Ha α*-gal jelöljük az A* ponthoz tartozó forgásszöget, az AA* egyenes állása 12(α+α*+π), és mivel ez merőleges BC-re, azért az α, β, γ, α* forgásszögekre
12(α+α*+π)-12(β+γ+π)=π2±kπ
teljesül, ahol k alkalmas egész szám. Az α* forgásszög alkalmas megválasztásával elérhető, hogy k=0, azaz
α*=β+γ-α+π
legyen.
3. Mivel az A*M egyenes állása 12(α*+μ+π), ezt az egyenest a BC-re tükrözve, a képének az állása azzal az ω-val jellemezhető, amelyre ω és 12(α*+μ+π) számtani közepe egyenlő 12(β+γ+π)-vel, azaz amelyre
ω=α+β+γ-μ2.
Ez az α, β, γ változók szimmetrikus függvénye, tehát ez jellemzi a B*M egyenes AC-re vonatkozó és a C*M egyenes AB-re vonatkozó tükörképének az állását is (amint azt bizonyítani akartuk), és egyben ez határozza meg az M-hez tartozó sM Simson-egyenes állását is.
4. Ha az α*-ra fent kapott eredményben α helyére μ-t írunk, megkapjuk az A' pont α' forgásszögét:
α'=β+γ-μ+π.
Ha pedig az ω-ra kapott eredményben μ helyére ezt az α'-t írjuk, kapjuk az A'-höz tartozó Simson egyenes állását:
ωA=α+μ-π2.
Ennek és a BC egyenes állását jellemző forgásszögnek a számtani közepe a
ϱ=α+β+γ+μ4,
ha tehát BC-t egy ϱ állású egyenesre tükrözzük, az A'-höz tartozó Simson-egyenessel párhuzamos egyenest kapunk.
Mivel ϱ az α, β, γ változók szimmetrikus függvénye, ha a CA és AB egyeneseket a ϱ állású egyenesre tükrözzük, akkor a B'-höz, illetve C'-höz tartozó Simson-egyenessel párhuzamos egyenest kapunk. Ezt kellett bizonyítanunk.