Kezdőlap


Feladat:	Pontversenyen kívüli P.107	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1972/április, 169 - 171. oldal		PDF \| MathML
Témakör(ök):	Rekurzív eljárások, Kombinatorikus geometria síkban, Parabola egyenlete, Kúpszeletek érintői, Szögfüggvények, síkgeometriai számítások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/május: Pontversenyen kívüli P.107

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A parabolához a $P (t$ , $t^{2} + 1$ ) pontban fektetett érintő egyenlete

\begin{matrix} y - (t^{2} + 1) = 2 t (x - t), \end{matrix}

eszerint az érintő az

x

tengelyt az

\begin{matrix} x = \frac{t^{2} - 1}{2 t} \end{matrix}

abszcisszájú

Q

pontban metszi. (

t = 0

kizárható, mert a (0; 1)-beli érintő nem metszi az

x

tengelyt, nem jön szóba

P_{i}

-ként.) Eszerint a feladat a (

P_{1}

P_{2}

...

P_{n}

) pont-

n

-es abszcisszáiból álló

T

(

t_{1}

t_{2}

...

t_{n}

) szám‐

n

-esre azt követeli, hogy

i = 1

, 2,

...

n - 1

mellett teljesüljön

\begin{matrix} t_{i + 1} = \frac{t_{i}^{2} - 1}{2 t_{i}}, \end{matrix}

(1)

és az innen

i = n

mellett adódó

t_{n + 1}

egyenlő legyen

t_{1}

-gyel.
Megoldásunk alapja az a (szerencsés) észrevétel, hogy ha

α_{i}

olyan szög, melyre

ctg α_{i} = t_{i}

, akkor

\begin{matrix} t_{i + 1} = \frac{{ctg}^{2} α_{i} - 1}{2 ctg α_{i}} = ctg 2 α_{i}, \end{matrix}

továbbá az, hogy minden valós

t_{1}

számhoz egyértelműen található olyan

α_{1}

, melyre

0 < α_{1} < π

és

ctg α_{1} = t_{1}

. Ekkor a

t_{i}

számok előállíthatók

α_{1}

felhasználásával:

\begin{matrix} t_{i} = ctg 2^{i - 1} α_{1}, \end{matrix}

és a

t_{n + 1} = t_{1}

követelmény így alakul:

\begin{matrix} ctg 2^{n} α_{1} = ctg α_{1} . \end{matrix}

Eszerint

2^{n} α_{1}

és

α_{1}

különbsége a

π

-nek egész számú többszöröse:

\begin{matrix} (2^{n} - 1) α_{1} = k π, α_{1} = k \cdot \frac{π}{2^{n} - 1}, \end{matrix}

ahol, tekintettel a

0 < α_{1} < π

előírásra

\begin{matrix} 0 < k < 2^{n} - 1. \end{matrix}

Mindezek szerint minden, a feladat követelményeinek eleget tevő

P_{i}

Q_{i}

pont-

n

-es egy

\begin{matrix} t_{1} = ctg \frac{k π}{2^{n} - 1} (k = 1, 2, ..., 2^{n} - 2) \end{matrix}

kezdőértékű és az (1) rekurzióból számított

T

szám‐

n

-eshez tartozik hozzá, és megfelelő pont‐

n

-est csak ilyen szám‐

n

-es ad.
A megfelelő pont‐

n

-esek száma természetesen kisebb, mint

2^{n} - 2

, hiszen minden pont‐

n

-est legalább 2 különböző pontja alapján kapunk meg, nem lehet tehát

P_{i + 1} \equiv P_{i}

, tehát

Q_{i + 1} \equiv Q_{i}

sem; viszont ‐ mint az 1660. feladatban^{$^{*}$} láttuk ‐

n = 2

esetén már van megoldása feladatunknak [és az minden

n = 2 m

(páros szám) esetén megfelel].

n = 6

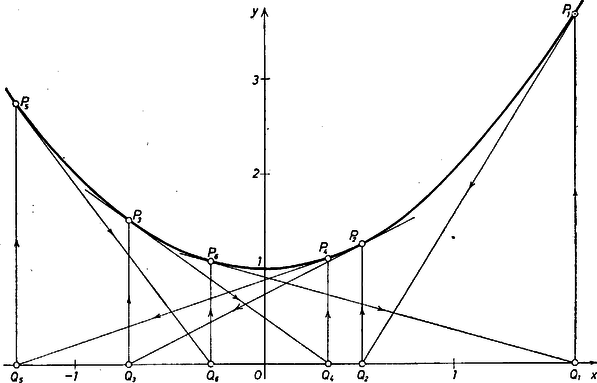
esetén ‐ mint könnyen látható ‐ a

\begin{matrix} k = 1, 3, 5, 7, 11, 15, 19, 23, 31 \end{matrix}

értékek 6 egymástól különböző pontból álló rendszereket adnak; a

\begin{matrix} k = 21 \end{matrix}

érték mellett

P_{3} \equiv P_{5} \equiv P_{1}

és

P_{4} \equiv P_{6} \equiv P_{2}

(ez az 1660. feladat megoldása,

21 / (2^{6} - 1) = 1 / 3

); végül a

\begin{matrix} k = 9, 27 \end{matrix}

értékek mellett pedig

P_{1}

P_{2}

P_{3}

különböző egymástól,

P_{4} \equiv P_{1}

, és innen kezdve a pontok ismétlődnek. Eszerint a különböző pont‐6-osok száma 12. (Felfogás dolga, hogy az utóbbi két típusú pontrendszert elfogadjuk vagy kizárjuk. A feladat nem zárta ki, hogy ugyanaz a pont többször szerepelhessen a rendszerben.) Az ábra a

k = 11

mellett adódó pontrendszert mutatja be,

x

-tengely menti nyújtással

^{$^{*}$}Lásd a megoldást K. M. L. 39. (1969) 128.