Kezdőlap


Feladat:	Pontversenyen kívüli P.106	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bacsó Gábor , Kovács István
Füzet:	1972/február, 73 - 74. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Geometriai transzformációk, Sorozat határértéke, Két pont távolsága, szakasz hosszúsága, Teljes indukció módszere, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/május: Pontversenyen kívüli P.106

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A tetszőleges $P$ pont $f (P)$ képét röviden $P'$ -vel jelöljük.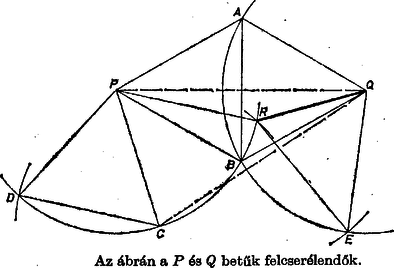
a) Megmutatjuk, hogy ha $P Q = \sqrt[]{3}$ , akkor $P' Q' = \sqrt[]{3}$ . Legyenek a $P$ körüli, egységsugarú $k$ körnek és a $Q$ középpontú, egységsugarú körnek a metszéspontjai $A$ és $B$ (1. ábra), ekkor az $A P$ , $A Q$ , $B P$ , $B Q$ és $A B$ szakaszok hossza egységnyi, e szakaszok képeinek a hossza is egységnyi.

1. ábra

Eszerint

A' B' P'

és

A' B' Q'

egységoldalú szabályos háromszögek, tehát

Q'

vagy azonos

P'

-vel vagy tőle

\sqrt[]{3}

távolságra van. Eddig tehát azt láttuk be, hogy ha két tetszőleges pont távolsága

\sqrt[]{3}

, akkor képeik távolsága vagy 0 vagy

\sqrt[]{3}

.
Legyen

C

P

körüli,

\sqrt[]{3}

sugarú kör, és a

Q

körüli, egységsugarú kör egyik metszéspontja. Így a

P' C'

szakasz hossza vagy 0 vagy

\sqrt[]{3}

, másrészt

Q' C' = 1

. Ha

Q'

azonos volna

P'

-vel, akkor a

P' C'

szakasz hosszának egyrészt 1-gyel, másrészt 0-val vagy

\sqrt[]{3}

-mal kellene egyenlőnek lennie, ami nyilvánvalóan lehetetlen. Így csak

P' Q' = \sqrt[]{3}

lehet. Ezt akartuk bizonyítani.
b) Hasonlóan láthatjuk be, hogy ha egy leképezés megtartja az

a

távolságot (azaz ha

P Q = a

-ból következik

P' Q' = a

), akkor az

\sqrt[]{3}

távolságot is megtartja. A mi leképezésünk megtartja a

\sqrt[]{3}

távolságot, tehát megtartja a

\sqrt[]{3} \cdot \sqrt[]{3} = 3

távolságot is, és általában a

{(\sqrt[]{3})}^{k}

távolságokat minden természetes

k

kitevő mellett.
Megmutatjuk, hogy leképezésünk minden természetes

n

számra megtartja az

n

távolságot. Már tudjuk, hogy ez igaz, ha

n = 3^{k}

. Válasszuk a

k

kitevőt úgy, hogy

n < 3^{k} = m

legyen, és tegyük fel, hogy

P Q = n

. Mérjük fel a

P Q

félegyenesre az egységnyi szakaszt

m

-szer, kapjuk a

P_{1}

P_{2}

...

P_{m}

pontokat (köztük

P_{n}

azonos

Q

-val). A

P' P'_{1}

P' P'_{2}

...

P'_{m - 1} P'_{m}

szakaszok hossza egységnyi, és

P' P'_{m} = m

, ez csak úgy lehet, ha a

P'

P'_{1}

...

P'_{m}

egy egyenes egymást követő pontjai. Tehát a

P'_{n} = Q'

pont

P'

-től

n

távolságra van, amint azt bizonyítani akartuk. Általában, ha egy leképezés megtartja az

a

távolságot, akkor megtartja az

n a

távolságot is, ha

n

természetes szám.
Szükségünk van azonban annak megmutatására is, hogy leképezésünk az 1-nél kisebb távolságokat is megtartja. Ezt bizonyítjuk be a következő lépésben.
c) Térjünk vissza az 1. ábra pontjaihoz, és legyen

R

P C

egyenes

Q

-t tartalmazó oldalán az a pont, amelyre

C R = Q R = 1

. Könnyen látható, hogy

\begin{matrix} λ = P R = \frac{\sqrt[]{11} - \sqrt[]{3}}{2} < 1. \end{matrix}

Eddig beláttuk, hogy az

A'

B'

C'

P'

Q'

pontokból álló alakzat egybevágó az

A B C P Q

alakzattal. Megmutatjuk, hogy

R'

azonos az

A' B' C' P' Q'

alakzat

R

-nek megfelelő

R^{*}

pontjával. Mivel

Q' R' = C' R' = 1

, azért

R'

vagy

R^{*}

-gal, vagy

R^{*}

-nak a

Q' C'

egyenesre vonatkozó

D^{*}

tükörképével azonos. Viszont

\begin{matrix} P' D^{*} = \frac{\sqrt[]{11} + \sqrt[]{3}}{2} > 2, \end{matrix}

így elegendő megmutatni, hogy

P' R' ≦ 2

. Legyen

E

olyan pont, melyre

P E = E R = 1

. Akkor

P' R' ≦ P' E' + E' R' = 2

, állításunkat ezzel bebizonyítottuk.
A leképezés ezek szerint a

λ

távolságot is megtartja, és általában megtartja az

n λ^{k}

távolságot is, ahol

n

és

k

természetes számok.
d) Legyen

P Q = d

tetszőleges valós szám. Feltehetjük, hogy

d > 0

, hiszen a leképezés egyértelmű volta miatt

P \equiv Q

esetén

P' \equiv Q'

. Tetszőleges

ε > 0

-hoz van olyan

k

, hogy

λ^{k} < ε

válasszuk meg

n

-et úgy, hogy

\begin{matrix} n λ^{k} ≦ d < (n + 1) λ^{k} \end{matrix}

legyen. Mérjük fel a

P Q

félegyenesre a

λ^{k}

szakaszt

n

-szer, kapjuk a

P_{1}

P_{2}

...

P_{n}

pontokat, és legyen

R

olyan pont, melyre

P_{n - 1} R = R Q = λ^{k}

(2. ábra).

2. ábra

Akkor

P' R' ≦ P' P'_{1} + P'_{1} P'_{2} + ... + P'_{n - 2} P'_{n - 1} + P'_{n - 1} R' + R' Q' = (n + 1) λ^{k} < d + ε

Tehát tetszőleges

ε > 0

mellett

P' R' < d + ε

, ami csak úgy lehet, ha

P' R' ≦ d

. Ezzel beláttuk, hogy tetszőleges

X Y

szakaszra

X' Y' ≦ X Y

. Alkalmazzuk ezt a

P_{n} Q

szakaszra, kapjuk, hogy

\begin{matrix} P' Q' ≧ P' P'_{n} - P'_{n} Q' ≧ P P_{n} - P_{n} Q ≧ n λ^{k} - ε > d - 2 ε . \end{matrix}

Tehát

P' Q' ≧ P Q

is igaz, így

P' Q' = P Q

, feladatunk állítását ezzel bebizonyítottuk.