Kezdőlap


Feladat:	Pontversenyen kívüli P.104	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Füredi Zoltán , Komjáth Péter , Kópházi József , Kovács István
Füzet:	1972/május, 214 - 216. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Húrnégyszögek, Érintőnégyszögek, Vektorok lineáris kombinációi, Vektorok skaláris szorzata, Alakzatok köré írt kör, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/április: Pontversenyen kívüli P.104

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a bicentrikus négyszög csúcsait $A_{1}$ -gyel, $A_{2}$ -vel, $A_{3}$ -mal, $A_{4}$ -gyel, a köréje és a beléje írt körök középpontját $K$ -val, ill. $O$ -val, a beírt kört $k$ -val, $k$ érintési pontjait az $A_{1} A_{2}$ , $A_{2} A_{3}$ , $A_{3} A_{4}$ , $A_{4} A_{1}$ oldalakon rendre $B_{1}$ -gyel, $B_{2}$ -vel, $B_{3}$ -mal, $B_{4}$ -gyel, és az ${\vec{O B}}_{1}$ vektorokat $b_{i}$ -vel $(i = 1,2,3,4)$ . Ha a $b_{i}$ vektorokat $(+ 90^{\circ})$ -kal elforgatjuk, a pozitívkörüljárású négyszög oldalaival párhuzamos, egyenlő hosszúságú vektorokat kapunk, elegendő tehát megmutatni, hogy a $b_{1} + b_{2} + b_{3} + b_{4}$ vektor párhuzamos az $\vec{O K}$ vekt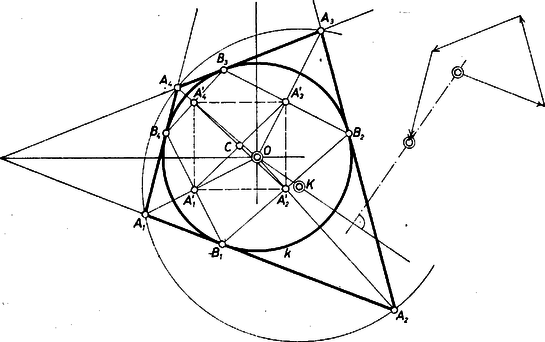orral.

Invertáljuk a négyszög köré írt kört

k

-ra, így az

A_{i}

csúcsok

k

-ra vonatkozó

A'_{i}

inverzén átmenő kört kapunk. Ismeretes, hogy az inverzió alapkörén kívül lévő pont inverzét megkapjuk, ha belőle érintőket húzunk az alapkörhöz, és vesszük az érintési pontok közti szakasz felezőpontját. Eszerint az

A'_{1}

A'_{2}

A'_{3}

A'_{4}

pontok rendre a

B_{4} B_{1}

B_{1} B_{2}

B_{2} B_{3}

B_{3} B_{4}

szakaszok felezőpontjai, az

A'_{1} A'_{2} A'_{3} A'_{4}

négyszög a

B_{1} B_{2} B_{3} B_{4}

négyszög középnégyszöge (azaz csúcsai

B_{1} B_{2} B_{3} B_{4}

-nek oldalfelező pontjai). Tehát az

A'_{1} A'_{2} A'_{3} A'_{4}

négyszög paralelogramma, másrészt csúcsai egy körön,

k

inverzén vannak.
Ez csak úgy lehet, ha ez a négyszög téglalap, és ekkor a köréje írható kör

C

középpontja a négyszög centruma, vagyis

\begin{matrix} \vec{O C} = \frac{1}{4} (\vec{O A'_{1}} + \vec{O A'_{2}} + \vec{O A'_{3}} + \vec{O A'_{4}}) = \frac{1}{4} (b_{1} + b_{2} + b_{3} + b_{4}) . \end{matrix}

Ha tehát a

b_{1} + b_{2} + b_{3} + b_{4}

összeg

0

vektor, akkor

C

azonos

O

-val, és így

K

is azonos

O

-val. Ha pedig ez az összeg nem

0

, akkor

C

és

O

különböző pontok és az

\vec{O C}

vektor párhuzamos

(b_{1} + b_{2} + b_{3} + b_{4})

-gyel. Ismeretes, hogy egy kör és inverzének középpontja az inverzió centrumán átmenő egyenest határoz meg, tehát az

O

C

K

pontok egy egyenesen vannak, és

O K

is párhuzamos

(b_{1} + b_{2} + b_{3} + b_{4})

-gyel. Ezzel az állítást bebizonyítottuk.

Megjegyzések. 1. Feladatunk állításán túlmenően azt is bebizonyítottuk, hogy a

(b_{1} + b_{2} + b_{3} + b_{4})

összeg akkor és csak akkor

0

, ha

O

és

K

azonosak.
2. A megoldásból az is kiolvasható, hogy

A_{1} A_{2} A_{3} A_{4}

akkor és csakis akkor bicentrikus négyszög, ha a

B_{1} B_{2} B_{3} B_{4}

négyszög átlói merőlegesek egymásra.

II. megoldás. A vektorok skaláris szorzatát felhasználva megmutatjuk, hogy feladatunk állítása minden bicentrikus sokszögre érvényes. Legyenek a sokszög csúcsai

A_{1}, A_{2}, ..., A_{n}

(és állapodjunk meg abban, hogy

A_{n + 1}

is az

A_{1}

csúcsot jelöli), a sokszög köré és a beléje írt körök középpontja legyen

K

és

O

. Jelöljük az

A_{i}

O

pontokhoz a

K

centrumból húzott helyvektorokat rendre

a_{i}

-vel és

p

-vel, az

A_{i} A_{i + 1}

oldalvektorral megegyező egyirányú egységvektort

e_{i}

-vel

(i = 1,2, ..., n)

. Feladatunk állítása ekvivalens azzal, hogy a

\begin{matrix} p \cdot (e_{1} + e_{2} + ... + e_{n}) \end{matrix}

skaláris szorzat értéke

0

, ezt fogjuk bizonyítani.
Az

A_{i}

csúcshoz tartozó belső szögfelező irányát a

({p-a}_{i})

vektor, az

A_{i}

-beli külső szögfelező irányát az

(e_{i - 1} + e_{i})

vektor adja meg

(i = 1,2, ..., n

; és

e_{0} = e_{n})

emiatt

\begin{matrix} (p - a_{i}) (e_{i - 1} + e_{i}) = 0. (i = 1,2, ..., n) \end{matrix}

Adjuk össze ezeket az egyenleteket, kapjuk, hogy

\begin{matrix} 2p \sum_{i = 1}^{n} e_{i} = \sum_{i = 1}^{n} a_{i} (e_{i u - 1} + e_{i}) . \end{matrix}

A jobb oldalon álló összeg egyenlő a

\begin{matrix} \sum_{i = 1}^{n} e_{i} (a_{i} + a_{i + 1}) \end{matrix}

összeggel (ahol

a_{n + 1} = a_{1})

, ennek viszont minden tagja

0

, hiszen

\frac{1}{2} (a_{i} + a_{i + 1})

A_{i} A_{i + 1}

szakasz felezőpontja, és

K A_{i} = K A_{i + 1}

miatt ennek a felezőpontnak a helyvektora merőleges az

A_{i} A_{i + 1}

oldalra. Állításunkat ezzel bebizonyítottuk.

Kópházi József (Tatabánya, Árpád Gimn., II. o. t. )

Megjegyzés. A most bizonyított állítás

n = 3

melletti speciális esete ekvivalens a P.51. probléma állításával, a fenti bizonyítás az erre adott II. megoldás általánosítása (K. M. L. 41. kötet 70. old.).