Kezdőlap


Feladat:	Pontversenyen kívüli P.95	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bacsó G. , Balog János , Ferró J. , Füredi Zoltán , Hermann P. , Katona E. , Komjáth P. , Komornik V. , Móri Tamás , Szendrei Ágnes , Szendrei Mária
Füzet:	1972/január, 25 - 26. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Beírt kör középpontja, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1971/február: Pontversenyen kívüli P.95

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $H = A B C$ háromszög beírt körét $k$ -val, középpontját $O$ -val. Azt kell megmutatnunk, hogy a $H_{1} = A_{1} B_{1} C_{1}$ háromszög kerületfelező egyenesei átmennek $O$ -n. Nyilván elegendő ezt az egyik kerületfelezőre belátnunk, vagyis elegendő azt bizonyítanunk, hogy a $C_{1} O$ egyenes felezi a $H_{1}$ kerületét (1. ábra).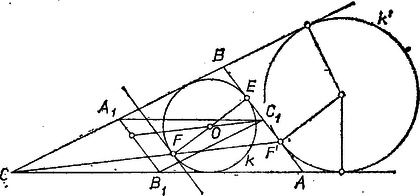

1. ábra

Jelöljük

H

-nak az

A B

oldalához hozzáírt külső érintő körét

k'

-vel, a

k

k'

körök

A B

-n levő érintési pontjait

E

-vel, illetve

F'

-vel. Mivel egy körhöz egy külső pontból húzott érintőszakaszok egyenlők, a

C A + A F'

és

C B + B F'

összegek egyenlők a

C

-ből

k'

-höz húzott érintőszakaszok hosszával, és így egymással is egyenlők. A

C F'

egyenes tehát felezi

H

kerületét. És mivel

H

és

H_{1}

centrálisan hasonlók (közös súlypontjukra nézve), azért megfelelő csúcsaikból kiinduló kerületfelező egyeneseik párhuzamosak egymással, elegendő tehát azt bizonyítanunk, hogy

C_{1} O ∥ C F'

.
A

k

és

k'

körök külső közös érintői

C

-ben metszik egymást, eszerint létezik olyan

C

centrumú kicsinyítés, amely

k'

-t

k

-ba viszi. Vigye ez a kicsinyítés az

F'

pontot

F

-be, ekkor

k

-nak

F

-beli érintője párhuzamos

A B

-vel. Emiatt

E F

k

átmérője és

O

felezi

E F

-et. Az

A E

B F'

szakaszok egyenlők, mert mind a kettő

H

félkerületének és a

B C

oldalnak a különbségével egyenlő. Emiatt

C_{1}

felezi az

E F'

szakaszt. Tehát a

C F'

-vel azonos

F F'

egyenest az

E

centrumból felére kicsinyítve

O C_{1}

-et kapjuk, így

O C_{1} ∥ F F'

, amint azt bizonyítani akartuk.

Balog János (Budapest, I. István Gimn.)

II. megoldás. Ismét azt bizonyítjuk be, hogy a

C_{1} O

egyenes azonos a

H_{1}

háromszög

C_{1}

csúcsához tartozó kerületfelező egyenesével. Forgassuk rá az

A_{1} B_{1}

egyenes

B_{1}

-en, illetve

A_{1}

-en túli meghosszabbítására a

B_{1} C_{1}

, illetve

A_{1} C_{1}

szakaszt, a kapott végpontokat jelöljük

A_{2}

-vel, illetve

B_{2}

-vel. Jelöljük az

A_{2} B_{2}

szakasz felezőpontját

C_{2}

-vel, ekkor

C_{1} C_{2}

nyilván

H_{1}

kerületfelezője. Az

A_{2} B_{1} C_{1}

háromszög egyenlő szárú, így az

A_{2}

-nél, és

C_{1}

-nél levő szögei egyenlőek. Az

A_{2}

-nél levő szöge viszont egyenlő az

A C_{1} A_{2}

szöggel is, mert váltószögek. Tehát

C_{1} A_{2}

felezi az

A C_{1} B_{1}

szöget és emiatt párhuzamos

H

-nak

B

-beli szögfelezőjével,

O B

-vel. Hasonlóan látható be, hogy

C_{1} B_{2}

párhuzamon

O A

-val (2. áb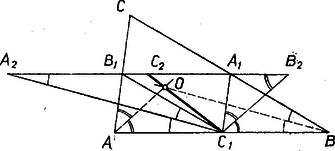ra).

2. ábra

Ezek szerint az

A B O

és

B_{2} A_{2} C_{1}

háromszögek megfelelő oldalai párhuzamosak, a háromszögek centrálisan hasonlók, és így párhuzamosak a megfelelő súlyvonalaik is. A

C_{1} O

C_{1} C_{2}

súlyvonalaknak

C_{1}

pontjuk közös, ezért ez a két egyenes azonos, és ez épp az, amit bizonyítani akartunk.

Füredi Zoltán (Budapest, Móricz Zs. Gimn.)

Megjegyzés. Feladatunk geometriailag jellemzi azt a pontot (a kerületfelező egyenesek metszéspontját), amelynek a P. 76-ban csak a létezését bizonyítottuk be. Összehasonlítva a két probléma megoldását, azt találjuk, hogy a mostaninak a megoldása egyszerűbb, noha benne többet bizonyítunk a létezésnél. Ez azonban nem meglepő: gyakori, hogy egy konkrét tulajdonságot, jellemzést általában könnyebb bizonyítani, mint valaminek a létezését.