Feladat: Pontversenyen kívüli P.91 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bálint László ,  Cseresnyés Mária ,  Göndőcs Ferenc ,  Komjáth Péter 
Füzet: 1972/március, 122 - 123. oldal  PDF  |  MathML 
Témakör(ök): Pont körüli forgatás, Kombinatorikus geometria síkban, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1971/január: Pontversenyen kívüli P.91

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Írjunk az ABCD=N négyzet AB, BC, CD, DA oldala fölé kifelé szabályos háromszöget, és legyen ezek új csúcsa rendre X, Y, Z, U. Ekkor N szimmetriái és a szerkesztés alapján XYZU=M is négyzet, és az N és M csúcsaiból álló pontnyolcas megfelel a követelménynek. Valóban, mindegyik négyzet 2 oldalfelezője azonos a másik négyzet 2 átlójának egyenesével, így a kívánt tulajdonság nyilvánvalóan mindig fennáll, ha egy szakasz két végpontjául ugyanazon négyzet csúcsai közül akár 2 szomszédosat, akár 2 szemben fekvőt választunk.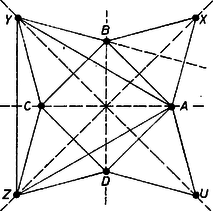

 

 
Ha pedig a szakasz végpontjainak egyike az N, másika az M csúcsai közül való, akkor pontrendszerünk szimmetriái alapján ‐ amelyek azonosak N és M szimmetriáival: 90∘-os forgás és 4 tükrözési tengely ‐ elég megmutatnunk az AX és AY szakaszok felező merőlegeséről, hogy átmegy a pontrendszer 2 pontján. Az YB egyenes az ABX szabályos háromszögnek magasságvonala, mert felezi az ABX szöget, hiszen BA-val bezárt szöge 180∘-(90∘+60∘)=30∘, tehát AX felező merőlegesén B is, Y is rajta van. Hasonlóan AY felező merőlegesének B is, Z is pontja, mert a szerkesztés folytán AB=YB, másrészt az ADZ és YCZ háromszögek egybevágók, és így AZ=YZ.
 

Cseresznyés Mária (Budapest, Fazekas M. Gyak. Gimn.)
 

Megjegyzések. 1. Elsőnek felvéve az M négyzetet, majd oldalai fölé befelé rajzolva a szabályos háromszögeket, N csúcsait kapjuk.
2. Várható, hogy a kívánt alakzat számos szimmetriát mutat ‐ hiszen (82)=28 felező merőlegesen kell biztosítani 2-2 pont illeszkedését, és ezen várhatóan könnyít, ha a felező merőlegesek közül egyesek egybeesnek (a fenti pontrendszerben 4 esetben 3-3 esik egybe). Ennek ellenére hosszadalmasnak ígérkezik megvizsgálni, van-e vajon más megfelelő pontnyolcas is. A feladat szerencsére csak az exisztenciáját kérdezte a pontrendszernek, unicitását nem.