Kezdőlap


Feladat:	Pontversenyen kívüli P.87	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bartolits István
Füzet:	1972/január, 21 - 23. oldal		PDF \| MathML
Témakör(ök):	Differenciálszámítás, Egyenesek egyenlete, Egyéb ponthalmazok a koordinátasíkon, Gördülés (Mozgási geometria), Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/december: Pontversenyen kívüli P.87

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A $g$ görbét asztroisnak nevezik, geometriailag többféleképpen származtatható, itt a következő származtatást vesszük alapul. Legyen a derékszögű koordinátarendszerben $P$ az origó középpontú, egységnyi sugarú $k$ kör tetszőleges pontja, ennek vetülete az $x$ tengelyen $A$ , az $y$ tengelyen $B$ és az $A B$ egyenesen $Q$ . Ha $P$ befutja a $k$ kört, akkor $Q$ mértani helye a $g$ görbe.
Valóban, legyen $P (a, b)$ , ahol

\begin{matrix} a^{2} + b^{2} = 1. \end{matrix}

(2)

Így

A (a, 0)

B (0, b)

, az

A B

egyenes egyenlete

\begin{matrix} b x + a y = a b, \end{matrix}

P

-n átmenő,

A B

-re merőleges egyenes egyenlete

\begin{matrix} a x - b y = a^{2} - b^{2}, \end{matrix}

és

Q

metszéspontjuk koordinátái

\begin{matrix} x_{Q} = a^{3}, y_{Q} = b^{3} . \end{matrix}

(3)

Eszerint

P

koordinátái a

Q

koordinátáival kifejezve

\begin{matrix} a = x_{Q}^{1 / 3}, b = y_{Q}^{1 / 3}, \end{matrix}

(4)

s mivel ezek kielégítik (2)-t,

Q

koordinátái között fennáll az adott (1).
Megfordítva, ha

Q (x, y)

g

-nek tetszőleges pontja, akkor a (4) koordinátákkal bíró

P (a, b)

pont rajta van

k

-n, és belőle kiindulva (3) szerint éppen

Q

-t kapjuk, állításunkat ezzel bebizonyítottuk.

b) Asztroisunk szimmetrikus az

x

y

tengelyekre és szögfelezőikre, mert ugyanez áll a származtatásában felhasznált

k

-ra és

x

y

tengelyekre.

g

-nek az

x

y

tengelyeken levő pontjai a

k

-n is rajta vannak ‐ ezeket

g

csúcsainak szokás nevezni ‐, minden más pontja a származtatás szerint a

k

belsejében van. Megmutatjuk, hogy

g

-hez a tetszőleges belső

Q

pontjában húzott érintő azonos a származtatásában szereplő

A B

egyenessel. A szimmetria alapján elég a bizonyítást egy olyan pontra elvégezni, amely az I. síknegyed szögfelezője és az

x

tengely pozitív fele közti (

45^{\circ}

-os) szögtartományban van, vagy magán a szögfelezőn, azaz

x \geq y > 0

és így (3) alapján

a \geq b > 0

;

P

is a mondott szögtartományban van.

Q

ordinátája mint az abszcissza függvénye (1)-ből

\begin{matrix} y = y (x) = {(1 - x^{2 / 3})}^{3 / 2}, \end{matrix}

és ez a

0 < x < 1

intervallumban differenciálható. Deriváltja, vagyis a görbe érintőjének iránytangense

\begin{matrix} y' (x) = \frac{3}{2} {(1 - x^{2 / 3})}^{1 / 2} \cdot (- \frac{2}{3}) x^{- 1 / 3} = - {(\frac{y}{x})}^{1 / 3}, \end{matrix}

és ez (3) szerint egyenlő az

A B

egyenes meredekségével, (

- b / a

)-val, tehát

A B

valóban érinti

g

-t.

c) A feladatban említett 8 metszéspont között a szimmetria alapján van olyan, mely a mondott síknyolcadban van, legyen ez ismét

Q

, és az egyik négyzet

Q R S T

úgy, hogy

R

a II.,

T

a IV. síknegyedben van. Ekkor a

Q R

egyenes

Q

-ban érinti

g

-t, tehát azonos a fenti

A B

egyenessel, a

Q

-t kimetsző

P Q (⊥ A B)

egyenes pedig a négyzet

Q T

oldalegyenesével. Eszerint

T Q

átmegy

P

-n, másrészt

Q R

-nek az

O

origó körüli (

- 90^{\circ}

)-os elfordításával áll elő. Így

T Q

x

tengelyt a

b

abszcisszájú

B'

pontban, az

y

tengelyt a

- a

) ordirnátájú

A'

pontban metszi, és meredekségének kétféle kifejezéséből:

\begin{matrix} b : (a - b) = a : b, & (5) \\ a b = a^{2} - b^{2} . \end{matrix}

d) Mármost a keresett sugárra (3), valamint (2) felhasználásával

\begin{matrix} r^{2} = O Q^{2} = x^{2} + y^{2} = a^{6} + b^{6} = (a^{2} + b^{2}) (a^{4} - a^{2} b^{2} + b^{4}) = {(a^{2} + b^{2})}^{2} - 3 a^{2} b^{2} = 1 - 3 a^{2} b^{2}, \end{matrix}

másrészt (5)-ből négyzetreemeléssel hasonlóan

\begin{matrix} a^{2} b^{2} = a^{4} - 2 a^{2} b^{2} + b^{4} = 1 - 4 a^{2} b^{2}, a^{2} b^{2} = 1 / 5, \end{matrix}

tehát

r = \sqrt[]{2 / 5}

. Ezzel a megoldást befejeztük.

Megjegyzések. 1. A vizsgált

Q R S T

négyzethez vezető

P

pont (5) alapján úgy szerkeszthető, hogy az

U (1 / 2, 1)

pontot összekötjük

O

-val, ekkor az

X O U

szög felezője metszi ki

P

-t. Ugyanis

X O P ∢ = φ

jelöléssel

a = cos φ

b = sin φ

, ezekkel (5)-ből (1/2)

sin 2 φ = cos 2 φ

és

tg 2 φ = 2

. ‐ A feladatban említett másik négyzet

Q R S T

-nek az I. síknegyed felezőjére (az

y = x

egyenletű egyenesre) vonatkozó tükörképe.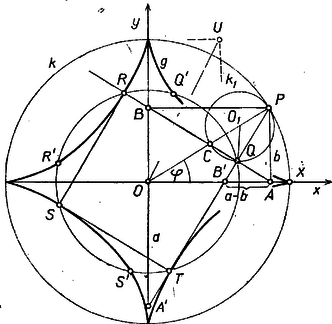

2. Ha

k

belsejében úgy gördítünk egy

1 / 4

sugarú

k_{1}

kört, hogy ez álladóan érintse

k

-t, akkor

k_{1}

minden pontja asztroist ír le (eszerint az asztrois az ún. hipocikloisok osztályának tagja). Speciálisan

g

-t az a pontja írja le

k_{1}

-nek, amely a gördülés folyamán

k

-nak az

x

tengelyen levő

X

pontjával kerül érintkezésbe. Amikor ez a pont áthalad

Q

-n, akkor

k_{1}

P

-ben érinti

k

-t. Az

O A P B

téglalap középpontját

C

-vel jelölve

C P

k_{1}

átmérője, ennek

O_{1}

felezőpontja a

k_{1}

középpontjának pillanatnyi helyzete,

A C P ∢ = 2 φ

Q O_{1} P ∢ = 4 φ

, és így

k_{1}

-nek

P Q

íve egyenlő hosszú

k

-nak

P X

ívével.