Kezdőlap


Feladat:	Pontversenyen kívüli P.86	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh Z. , Ferró József , Kirchner I.
Füzet:	1971/május, 214 - 216. oldal		PDF \| MathML
Témakör(ök):	Hamilton-út, -kör, Játékelmélet, játékok, Kombinációk, Klasszikus valószínűség, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/december: Pontversenyen kívüli P.86

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a keresett valószínűséget $p_{N}$ -nel. Mivel $5$ játékos lehetséges párosításainak a száma $(\binom{5}{2}) = 10$ , azért $10$ cédulát készítettek. Ezek közül az első $N$ játék számára

\begin{matrix} V_{N} = 10 \cdot 9 \cdot ... \cdot (11 - N) \end{matrix}

-féleképpen választhatjuk ki a cédulákat. Jelöljük

K_{N}

-nel azoknak a választásoknak a számát, amelyekben valamelyik három játékosnak mindhárom lehetséges párosítása szerepel. Ekkor, mivel az egyes választások egyformán valószínűek,

p_{N} = K_{N} / V_{N}

.-
Az első

N

játék tervét úgyis elkészíthetjük, hogy először egyszerre veszünk ki

N

cédulát, majd a választott cédulákat sorba rakjuk. A kiválasztó lépésben

v_{N} = (\binom{10}{N})

lehetőség közül választunk egyet, és minden választásnál

N!

-féle sorrendet készíthetünk. (Valóban,

V_{N} = v_{N} \cdot N!

). Egy játéksorozat kedvező volta nem függ a játék sorrendjétől, ha tehát

k_{N}

-nel jelöljük azoknak a választásoknak a számát, (a játékok sorrendjére való tekintet nélkül), amelyekben valamelyik három játékos mindhárom lehetséges párosítása szerepel, akkor

K_{N} = k_{N} \cdot N!

és

\begin{matrix} p_{N} = \frac{K_{N}}{V_{N}} = \frac{k_{N}}{v_{N}}, \end{matrix}

ahol, mint láttuk,

v_{N} = (\binom{10}{N})

, így elegendő

k_{N}

értékét meghatároznunk.
Ha

N < 3

, akkor

k_{N} = 0

, hiszen egy kedvező választásnak legalább három játékot tartalmaznia kell, így érthető, miért kérdi a feladat csak

N ≧ 3

mellett

p_{N}

értékét.
Ha

N = 3

, akkor kedvező választás csak valamelyik három játékos három játszmája lehet, így

k_{3}

annyi, ahányféleképpen ezt a három játékost az öt közül kiválaszthatjuk:

k_{3} = (\binom{5}{3})

, és

\begin{matrix} p_{3} = \frac{(\binom{5}{3})}{(\binom{10}{3})} = \frac{5 \cdot 4 \cdot 3}{10 \cdot 9 \cdot 8} = \frac{1}{12} . \end{matrix}

N = 4

, akkor egy kedvező választásban valamelyik három játékos három játszmáján kívül még egy tetszőleges játszma szerepel. Minden kedvező választáshoz csak egyféleképpen adható meg az a három játékos, akiknek minden játszmájuk szerepel a választásban, hiszen kétféle játékos-hármas összes játszmáinak a száma legalább

5

. A kedvező választásokban szereplő három játékost ismét

(\binom{5}{3})

-féleképpen választhatjuk, ezek három játékához a negyedik játszmát a többi

7

közül

7

-féleképpen adhatjuk meg, tehát

k_{4} = (\binom{5}{3}) \cdot 7

, és

\begin{matrix} p_{4} = \frac{(\binom{5}{3}) \cdot 7}{(\binom{10}{4})} = p_{3} \cdot \frac{7 \cdot 4}{7} = \frac{1}{3} . \end{matrix}

N = 5

mellett hasonló módszerrel

(\binom{5}{3})

(\binom{7}{2})

választást adhatunk meg (három játékos három játszmájához a maradék

7

játszma közül tetszőlegesen választva

2

továbbit), ezek azonban már nem mind különbözőek, hiszen azokat a választásokat kétszer is előállítottuk, amelyekben két játékos-hármas öt játéka van. Két játékos-hármas összes játszmáinak a száma akkor

5

, ha egy játszma mindkét csoportban szerepel. Ez csak úgy lehet, ha a két csoport két játékosa közös, vagyis a választásban

4

játékos

6

játszmája közül valamelyik ötöt adtuk meg. (A hatodik az a játszma, amelyet az a két játékos játszana egymással, akik csak egy-egy csoportban vannak benne.) A kétszer számolt választások száma tehát

(\binom{5}{4}) \cdot 6

, vagyis

\begin{matrix} k_{5} = (\binom{5}{3}) (\binom{7}{2}) - (\binom{5}{4}) \cdot 6, \end{matrix}

és

\begin{matrix} p_{5} = \frac{(\binom{5}{3}) (\binom{7}{2}) - (\binom{5}{4}) \cdot 6}{(\binom{10}{5})} = \frac{210 - 30}{252} = \frac{5}{7} . \end{matrix}

N ≧ 6

, egyszerűbb a kedvezőtlen választások

C_{N}

számát meghatározni a következő módon. Nem azt vizsgáljuk, hogyan lehet

N

játszmát kiválasztani úgy, hogy ne legyen köztük három játékos három játszmája, hanem azt, hogyan lehet

(10 - N)

játszmát megadni úgy, hogy a többi játszma között ne szerepeljen három játékos három játszmája. Egy ilyen választásban minden játékosnak szerepelnie kell, hiszen ha valamelyik nem szerepelne, akkor a többi négy játékos hat játszmája közül valamelyik hiányzana a választásból (hiszen

10 - N < 6

), ez a játszma és a benne szereplő két játékosnak a kihagyott játékossal játszott egy-egy játszmája három játékos három játszmája lenne, a többi

N

játszma tehát nem volna kedvezőtlen. Jelöljük a választásban szereplő egyik játszma játékosait

A

B

-vel. A többi három játékos

(C, D, E)

valamelyik játszmája ugyancsak szerepel a választásban, mondjuk a

C D

játszma. Láttuk, hogy az

E

játékosnak is szerepel valamelyik játszmája, és mivel

E

-nek a másik négy játékoshoz viszonyított szerepe még teljesen szimmetrikus, azért feltehetjük, hogy az

A E

játszmát választottuk. Ekkor még a

B C E

B D E

hármas egyetlen játszmáját sem választottuk, tehát még legalább egy játszmát választanunk kell, és az csak a bennük közös

B E

játszma lehet. Azt kaptuk, hogy a többi

(10 - N)

játszmát csak akkor választhatjuk meg kedvezőtlenül, ha

10 - N = 4

N = 6

, és ilyen esetben a választás akkor kedvezőtlen, ha benne három játékos három játszmája szerepel, és a negyedik játszma a másik két játékos játszmája. Így

C_{6} = (\binom{5}{3})

, és

C_{N} = 0

, ha

N > 6

, azaz

\begin{matrix} p_{6} & = 1 - \frac{(\binom{5}{3})}{(\binom{10}{4})} = 1 - \frac{1}{21} = \frac{20}{21}, \\ p_{7} & = p_{8} = p_{9} = p_{10} = 1. \end{matrix}

II. megoldásként minden szöveg nélkül egy "beszédes ábrát'' közlünk. Reméljük, hogy az ábra megfejtése ‐ kifejezőbb szóval: értelmezése ‐ tanulságos lesz az olvasók részére.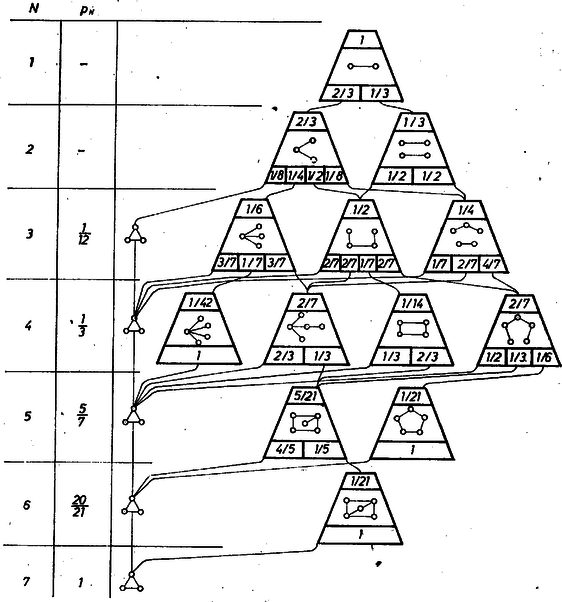