| Feladat: | Pontversenyen kívüli P.85 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Ábrahám L. , Füredi Zoltán , Göndőcs Ferenc , Szendrei Mária | ||
| Füzet: | 1972/február, 72 - 73. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorikus geometria síkban, Egyéb sokszögek geometriája, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1970/december: Pontversenyen kívüli P.85 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen olyan pontrendszer, amelyben nincs három, egy egyenesen levő, és nincs öt, egy konvex ötszöget meghatározó pont. Azzal igazoljuk a feladat állítását, hogy megmutatjuk: -nak legföljebb 8 pontja van. 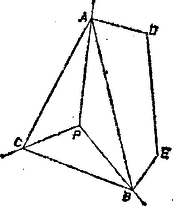 Így és pontjainak száma együttvéve legföljebb 7, elegendő tehát azt megmutatnunk, hogy -nak csak egy pontja lehet belsejében. Tegyük fel ezzel ellentétben, hogy -nak mondjuk a és pontja van belsejében. Ha négyszög, akkor a egyenes csak szemközti oldalait metszheti, hiszen ha -nak három csúcsa volna a egyenes egyik oldalán, ezek a , pontokkal együtt egy konvex ötszöget határoznának meg. Jelöljük csúcsait , , , -vel és válasszuk úgy a betűzést, hogy a félegyenes , a félegyenes az szakaszt messe (2. ábra). 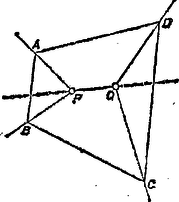 A fentiekhez hasonlóan látható be, hogy az , szögtartományban -nak csak egy‐egy csúcsa lehet. A , félegyenesek és a szakasz által határolt síkrészben viszont egyetlen csúcsa sem lehet -nak, különben az a , , , pontokkal együtt konvex ötszöget határozna meg. Ugyanígy a , félegyenesek és a szakasz által határolt síkrészben sem lehet csúcsa -nak, így ellentmondásra jutottunk, hiszen ezek szerint -nak csak két csúcsa lehetne. Ha háromszög, jelöljük a csúcsait , , -vel, és válasszuk úgy a betűzést, hogy a félegyenes a , a félegyenes az szakaszt messe (3. ábra). 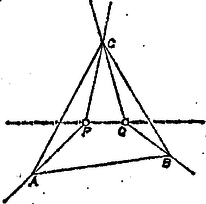 Ekkor a , félegyenesek és a szakasz által határolt síkrészben nem lehet csúcsa -nak, az , szögtartományokban pedig csak egy‐egy csúcsa lehetne. Ismét ellentmondásra jutottunk, állításunkat ezzel bebizonyítottuk. |