Kezdőlap


Feladat:	Pontversenyen kívüli P.84	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Reviczky János
Füzet:	1972/április, 166 - 169. oldal		PDF \| MathML
Témakör(ök):	Inverzió, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/november: Pontversenyen kívüli P.84

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Jelöljük adott (és egymástól páronként különböző) köreinket $k_{1}$ -gyel, $k_{2}$ -vel, $k_{3}$ -mal, a keresett inverzió alapkörét ‐ föltéve, hogy létezik ‐ $k$ -val, köreink erre invertált képeit $k'_{1}$ , $k'_{2}$ , $k'_{3}$ ,-vel, a középpontjaikon átmenő egyenest $e'$ -vel és ennek $k$ -ra való inverzét ‐ más szóval eredetijét ‐ $e$ -vel.
Mint tudjuk, $e$ akkor és csak akkor adódik egyenesnek, ha $e'$ átmegy a $k$ alapkör középpontján, és ekkor $e$ egybeesik $e'$ -vel (de nem pontról pontra azonosak), különben pedig körnek adódik $e$ . Ebből mindjárt látjuk, hogy ha a kívánt tulajdonság már az eredeti $k_{1}$ , $k_{2}$ , $k_{3}$ körhármasra fennáll ‐ vagyis középpontjaik egy $e$ egyenesen vannak ‐, akkor található a kívánt $k$ alapkör, éspedig középpontjául választható $e$ -nek bármely pontja, kivéve a $k_{j}$ -vel ( $j = 1$ , 2, 3) való metszéspontjait ‐ hiszen kör inverz képe akkor és csak akkor nem kör, ha átmegy az inverzió centrumán ‐, $k$ sugara pedig tetszőleges.
Az adott $k_{j}$ körök középpontjai általában nincsenek egy egyenesen. Ilyenkor azt a tulajdonságot, hogy a $k'_{j}$ körök középpontjai az $e'$ egyenesen vannak, a következő alakban használjuk majd fel: $e'$ merőlegesen metszi $k'_{j}$ mindegyikét. Ugyanis az inverzió szögtartó, részletesebben kimondva: körök, egyenesek képei közti szög egyenlő az eredeti vonalak közti megfelelő szöggel; az utóbbit úgy értve, hogy kör helyett mindig a metszéspontbeli érintőjét tekintjük a szög megfelelő szárának. Eszerint már $e$ -nek merőlegesen kell metszenie $k_{j}$ mindegyikét, és ekkor a keresett $k$ szerepére megfelel minden olyan kör, melynek középpontja $e$ -n van. (De $k$ középpontjának ismét nem szabad egybeesnie $e$ és a $k_{j}$ körök közös pontjaival, mert feladatunk csak olyan megoldást fogad el, melyben mindegyik $k_{j}$ képe is kör.)
A kérdés tehát erre redukálódott: van-e olyan $e$ kör, amely $k_{j}$ ( $j = 1$ , 2, 3) mindegyikét merőlegesen metszi. Fel fogjuk használni a következő fogalmakat: pontnak körre vonatkozó hatványa, két kör hatványvonala, három kör hatványpontja. Ezeket és néhány rájuk vonatkozó tételt itt összefoglalunk.^{$^{*}$}

P

pontnak az

O

középpontú,

r

sugarú

k

körre vonatkozó hatványa

P O^{2} - r^{2}

(

k

belső pontjaira negatív,

k

pontjaira 0, külső pontokra pedig pozitív és egyenlő a

P

-ből

k

-hoz húzott érintőszakasz négyzetével.) ‐ Azoknak a pontoknak a mértani helye, amelyeknek az

O_{1}

és

O_{2}

középpontú körökre vonatkozó hatványa egyenlő, egyenes, mely merőleges az

O_{1} O_{2}

centrálisra. Ezt a mértani helyet más néven a két kör hatványvonalának nevezzük. Koncentrikus köröknek nincs hatványvonaluk. Két egymást metsző kör hatványvonala a metszéspontjaikat összekötő egyenes. Két egymást érintő kör hatványvonala a közös pontjukban húzott érintőjük. ‐ Három kör páronként vett hatványvonalai ‐ ha a három középpont nincs egy egyenesen ‐ egy pontban, a három kör ún. közös hatványpontjában metszik egymást.

Ezekből következik, hogy három körhöz ‐ melyek középpontjai nincsenek egy egyenesen (vagyis amilyen körhármas esetére még nem adtuk megoldását feladatunknak) ‐ létezik egy és csak egy olyan pont, melynek a három körre vonatkozó hatványa egyenlő. Ez vagy mindhárom körre nézve külső pont, vagy mindháromnak közös belső pontja, illetve a közös pontjuk, ha a három kör egy ponton megy át; e háromféle esetnek megfelelően a hatvány közös értéke, pozitív, negatív, ill. 0.
Mármost redukált kérdésünkre a válasz az első esetben igenlő, az utóbbi kettőben viszont nem létezik a keresett inverzió. Ugyanis az első esetben a hatványpontból a három körhöz húzott érintőszakasz egyenlő, és ezzel a hosszúsággal mint sugárral a hatványpont körül írt kör a három kört merőlegesen metszi. Ezt mutatja az 1. ábra.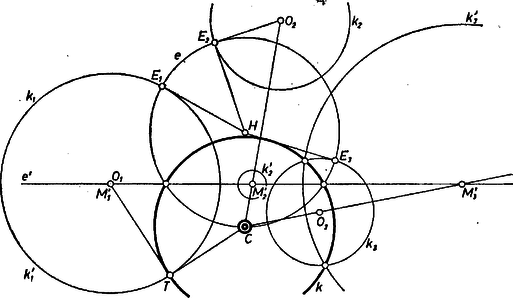

1. ábra

H

a hatványpont,

H E_{1} = H E_{2} = H E_{3}

az érintőszakaszok. A

H

körüli,

E_{1}

-en átmenő

e

körön választottuk az inverzió

C

centrumát,

k

-nak

C T

sugarát pedig speciálisan úgy, hogy

k

merőlegesen messe

k_{1}

-et; így

k'_{1}

mindjárt azonos magával

k_{1}

-gyel. A körök középpontjai

O_{j}

, képeiké

M_{j}

, az

O_{j} M_{j}

(

j = 2

, 3) egyenes átmegy

C

-n. (Magának

H

-nak a szerkesztését nem tüntettük fel. E célra pl.

k_{1}

és

k_{2}

hatványvonala a hatványpont idézett tétele szerint úgy szerkeszthető, hogy véve egy mindkettőt metsző

k_{4}

kört, a

k_{1}

k_{4}

és a

k_{2}

k_{4}

körpár közös húregyeneseinek metszéspontjából merőlegest állítunk az

O_{1} O_{2}

egyenesre.)

b) A feladat második kérdésének előkészítéséül vegyük észre, hogy két kör sugara akkor és csak akkor egyenlő, ha van olyan (közönséges) tengelyes tükrözés, amely őket egymásba viszi át (ti. a középpontjaik közti szakasz felező merőlegesére való tükrözés ilyen; ha pedig koncentrikusak a körök, akkor bármely, a centrumukon átmenő egyenes ilyen).
Felhasználjuk továbbá P. 31 probléma^{$^{*}$} segédtételét, a következő alakban. Ha

P

f

Q

egy tárgy‐tükör‐kép rendszer, ahol

f

egy inverzió alapköre vagy egy egyenes ‐ azaz

P

és

Q

egymás képei

f

-re ‐, továbbá egy inverzióban vagy közönséges tengelyes tükrözésben

P

f

Q

képe rendre

P'

f'

Q'

, akkor

P'

f'

Q'

is egy tárgy‐tükör‐kép rendszer. (Itt tehát 3 inverzióról van szó, amelyek közt tengelyes tükrözések is fölléphetnek.)
Ezeket egybevetve, az adott köreink közül választott kettőnek ‐ mondjuk a

k_{1}

-nek és

k_{2}

-nek ‐ valamely

k

körre való invertált képei,

k'_{1}

és

k'_{2}

akkor és csak akkor lesznek egyenlő sugarúak, ha van olyan inverzió vagy tengelyes tükrözés, mely

k_{1}

-et és

k_{2}

-t egymásba viszi át. Ha van, akkor ennek az inverziónak az

f

alapkörét, ill. tengelyét egy

f'

egyenessé kell transzformálnunk a keresett

k

körre való invertálás útján, ehhez pedig elég

k

centrumát

f

-en úgy megválasztani, hogy ne legyen rajta egyidejűleg se

k_{1}

-en, se

k_{2}

-n.
Állítjuk, hogy a sík bármely két,

k_{1}

és

k_{2}

köréhez van olyan

k_{i}

alapkör, amelyre való invertálás a két kört egymásba viszi át. A bizonyítást csak vázoljuk.
Egymáson kívül álló körök esetében a keresett inverzió centruma csak a körök

S

külső hasonlósági középpontja lehet, csak

S

-nek van meg az a tulajdonsága, hogy a belőle kiinduló félegyeneseknek

k_{1}

-gyel ugyanannyi közös pontjuk van, mint

k_{2}

-vel: vagy 2 vagy 1 vagy 0. (Ez nyilván szükséges feltétel.)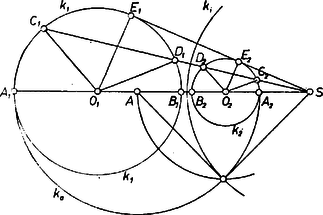

2. ábra

A 2. ábra jelöléseivel

O_{1} C_{1} ∥ O_{2} D_{2}

O_{1} D_{1} ∥ O_{2} C_{2}

, a párhuzamos szelők tétele alapján

\begin{matrix} S C_{1} : S D_{2} = S O_{1} : S O_{2} = S D_{1} : S C_{2} . \end{matrix}

Másrészt a külső pontból húzott szelő és érintő tétele alapján

\begin{matrix} S C_{i} \cdot {S D}_{i} = S A_{i} \cdot {S B}_{i} = S E_{i}^{2}, (i = 1, 2) \end{matrix}

és ezekből

\begin{matrix} S C_{1} \cdot S C_{2} = S D_{1} \cdot S D_{2} = \frac{S E_{1}^{2}}{S C_{1}} \cdot \frac{S E_{2}^{2}}{S C_{2}}, S C_{1} \cdot S C_{2} = S E_{1} \cdot S E_{2}, \end{matrix}

állandó, tehát a kívánt

k_{i}

alapkör sugara

S E_{1}

és

S E_{2}

mértani közepe. A tételt tudva, megszerkeszthető

k_{i}

abból is, hogy az

A_{1}

A_{2}

pontok egymásba mennek át, ezért az

A_{1} A_{2}

átmérőjű

k_{a}

kör önmagába megy át és ‐ mint az 1. ábrán

k_{1}

esetében ‐ az alapkör átmegy az

S

-ből

k_{a}

-hoz húzott érintő

T

érintési pontján. ‐ Meggondolásunk egymással kívülről érintkező körökre is érvényes. ‐

S

csak akkor nem létezik, ha

k_{1}

és

k_{2}

sugarai egyenlők, ekkor

O_{1} O_{2}

felező merőlegese lép

k_{i}

helyére.
Hasonlóan látható be állításunk arra az esetre, ha

k_{2}

k_{1}

belsejében van. Ekkor az inverzió centruma

k_{1}

-nek és

k_{2}

-nek

S'

belső hasonlósági pontja (ahol a párhuzamos és ellentétes irányú sugaraik végpontjait összekötő egyenesek összefutnak), a meggondolásban

S

helyére

S'

és

E_{i}

helyére

F_{i}

teendő, az

S'

-ben

O_{1} O_{2}

-re állított merőlegesnek

k_{i}

-vel való metszéspontja. Ekkor

k'_{i}

sugara az

S' F_{1}

S' F_{2}

szakaszok mértani közepe. (

S' F_{i}^{2}

S'

pont

k_{i}

-re vonatkozó hatványának abszolút értéke:

S' F_{i}^{2} = O_{i} F_{i}^{2} - S' O_{i}^{2} = r_{i}^{2} - S' O_{i}^{2}

.) A fentebbi szerkesztés is érvényes,

A_{1}

és

A_{2}

a körök párhuzamos és egyirányú sugarainak végpontjai az

O_{1} O_{2}

egyenesen. ‐ Érvényes e meggondolás egymással belülről érintkező körökre, valamint két koncentrikus körre is.

Végül ha

k_{1}

-nek és

k_{2}

-nek két közös pontja van, akkor mindkét meggondolás érvényes, két olyan inverziós alapkör van, mely

k_{1}

-et és

k_{2}

-t egymásba viszi át. A körük metszéspontjain mindkét alapkör átmegy (3. ábra).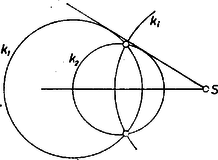

3. ábra

Visszatérve feladatunk második kérdéséhez,

k_{1}

k_{2}

k_{3}

közül kettőt kiszemelve és a fent mondott

f

-nek véve az őket egymásba átvivő inverzió alapkörét (vagy tükrözés tengelyét),

f

és a fenti ‐ ha van ilyen ‐

e

kör közös pontja mint inverzió centrum teljesíti a követelményt, tetszőleges sugár mellett.

^{$^{*}$} A bizonyítások megtalálhatók pl. a következő helyen: Tolnai Jenő: Érdekes matematikai gyakorló feladatok. II. kötet. Középiskolai Szakköri Füzetek. Tankönyvkiadó. Budapest, 1971. 22‐23. oldal.

^{$^{*}$}A probléma ‐ megoldását ‐ lásd K. M. L. 39. (1969) 155‐156. ‐ új bizonyítást kívánt a P. 12. problémára a következő segédtétel alapján. Ha $g$ egy, a $C$ ponton nem átmenő kör vagy egyenes, és egy $P$ pontnak $g$ -re vonatkozó inverze ‐ ill. tükörképe, ha $g$ egyenes ‐ a $Q$ pont, továbbá $g$ -nek, $P$ -nek, $Q$ -nak egy $C$ középpontú körre vonatkozó inverze $g_{1}$ , $P_{1}$ , ill. $Q_{1}$ , akkor $P_{1}$ -nek $g_{1}$ -re vonatkozó inverze $Q_{1}$ . Maga a P. 12. probléma pedig ‐ megoldását lásd K. M. L. 38. (1969) 171‐172. ‐ a következőt kívánta. Bizonyítandó, hogy ha $g$ egy a $C$ ponton nem átmenő kör vagy egyenes, akkor egy $C$ középpontú $k$ körre vett inverz képének a középpontját úgy kaphatjuk meg, hogy $C$ -nek $g$ -re vonatkozó inverz képét (ill. tükörképét, ha $g$ egyenes) invertáljuk $k$ -ra. ‐ Megjegyezzük, hogy a P. 31.-beli segédtétel bizonyítása nem használta fel, hogy $g$ nem megy át $C$ -n (erre a föltevésre csak a P. 12.-ben volt szükség, különben ugyanis $g$ képe mindenképpen egyenes lenne, és nem volna értelme beszélni $g$ középpontjáról). Ennélfogva a segédtétel érvényes akkor is, ha $g$ átmegy $C$ -n.