|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ismeretes, hogy a sík azon pontjainak a mértani helye, melyeknek két különböző ponttól, -tól és -től mért távolságainak az aránya egy adott pozitív szám: , az szakasz felezőmerőlegese, ha ; ha pedig , akkor egy kör, melyre -t invertálva -t kapjuk. A továbbiakban -et egyszerűség kedvéért -vel is jelöljük, hogy ne kelljen a két esetet megkülönböztetni. Könnyen belátható az is, hogy két olyan részre vágja a síkot, amelyek közül az -t tartalmazó részben a -t tartalmazó részben pedig (Ez mellett közismert, mellett pedig az idézett bizonyításból kiolvasható, hiszen ott épp a esetre vezettük vissza a esetet is.)
Ezek szerint, ha találunk az egyenesen olyan pontot, hogy az egyenes -től különböző pontjai a arányhoz tartozó -nak -t tartalmazó oldalán vannak, akkor tetszőleges, től különböző pontjában tehát a vizsgált aránynak -ben minimuma van; és megfordítva, ha (1) teljesül, akkor az egyenes től különböző pontjai -nak -t tartalmazó oldalán vannak.
Hasonlóan látható be, hogy a aránynak akkor és csakis akkor van a pontban maximuma, ha -nek től különböző pontjai a arányhoz tartozó -nak -t tartalmazó oldalán vannak.
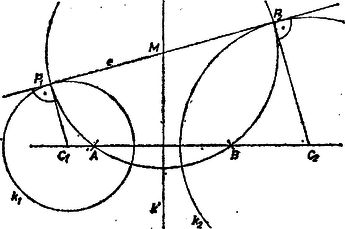
Az, hogy pontjai egyikük kivételével egyik oldalán legyenek, csak akkor lehet, ha kör, és érinti -t. Tegyük fel először, hogy és metszik egymást, és jelöljük a metszéspontot -mel, az középpontú, -n és -n átmenő kört -val. Tetszőleges mellett a alapkörű inverzió -t -be viszi, tehát -t önmagába viszi át (hiszen és metszi egymást, és e metszéspontok a helyükön maradnak). Emiatt merőleges -ra, és az -ből -hoz húzott érintők érintési pontjai rajta vannak -n. A keresett és pont tehát csak és metszéspontja lehet. Belátjuk, hogy a -nek -t tartalmazó oldalán levő metszéspont, pedig a másik metszéspont. Jelöljük ezeket a pontokat átmenetileg rendre -gyel és -vel; megmutatjuk, hogy azonosak a keresett pontokkal.
Messe az -re merőleges, -n átmenő egyenes az egyenest -ben, és legyen a középpontú, -n átmenő kör . A szerkesztés alapján merőlegesen metszi -t, így -nak a -n átmenő egyenesen levő és pontjait a -re való invertálás egymásba viszi át. Emiatt az arányhoz tartozó Apollóniosz‐kör . Az pont a belső pontja, -nek pedig külső pontja, tehát azonos -vel .
Ha tehát és metszi egymást, akkor a minimális és maximális arányt adó pontokat a metszéspontjuk körül rajzolt, -n átmenő kör metszi ki -ből, a -nek -t tartalmazó oldalán kapjuk a minimumot, a másik oldalon a maximumot.
Ha és azonosak, akkor -n az arány állandó, tehát nincs sem maximuma, sem minimuma. Ha párhuzamos -vel, akkor az , pontokhoz tartozó bármelyik kört csak az egyenesen levő pontban érintheti, hiszen is, is szimmetrikus az egyenesre. Jelöljük és az egyenes metszéspontját -gyel, vagy -vel aszerint, hogy az a -nek -t tartalmazó vagy -t nem tartalmazó oldalán van. Az első esetben -ben minimuma van az aránynak, hiszen a en átmenő, az , pontokhoz tartozó Apollóniosz-kör belsejében tartalmazza az pontot, hasonlóan látható, hogy a második esetben -ben maximum van. Mivel szélső érték csak és valamely érintési pontjában lehet, ezekben az esetekben maximum, illetve minimum nincs.
| Katona Endre (Szeged, Radnóti M. Gimn., IV. o. t.) |
Megjegyzések. 1. A megoldásban maximumnak (illetve minimumnak) azt a függvényértéket tekintettük, amelyiknél a vizsgált függvény minden más értéke határozottan kisebb (illetve nagyobb). A kapott eredmény akkor is helyes (csak kicsit hosszabban bizonyítható), ha e definícióban "kisebb'' (illetve "nagyobb'') helyett a "kisebb vagy egyenlő'' (illetve "nagyobb vagy egyenlő'') kifejezést használjuk; kivéve azt az esetet, amikor és azonosak, ekkor ugyanis az utóbbi definíció szerint minden pontjában maximum is és minimum is van.
2. A szerkesztés ‐ mint látjuk ‐ egyszerű, az indokolás viszont hosszabb. Erre az ellentétre utaltunk már az 1334. gyakorlatban (K. M. L. 42 (1971) 211.).
Lásd pl. Bártfai‐Tusnády: Pályázat az inverzióról. K. M. L. 42 (1971) 1‐7. |
 PDF |
PDF |  MathML
MathML