Kezdőlap


Feladat:	Pontversenyen kívüli P.78	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Breuer Péter , Ferró J. , Füredi Zoltán , Göndőcs Ferenc , Komjáth Péter , Less György , Reviczky János , Stachó Balázs
Füzet:	1971/október, 70 - 72. oldal		PDF \| MathML
Témakör(ök):	Rekurzív eljárások, Kombinatorikus geometria síkban, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/október: Pontversenyen kívüli P.78

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük általában $H (n)$ -nel az $n$ pont által meghatározott hegyesszögű háromszögek lehető legnagyobb számát, vagyis $H (n)$ -nek megvan a következő két tulajdonsága: a) bárhogy adunk meg $n$ pontot a síkon (kölcsönös helyzetük szerint), az általuk meghatározott hegyesszögű háromszögek száma nem nagyobb, mint $H (n)$ , b) meg tudunk adni $n$ pontot úgy, hogy az általuk meghatározott hegyesszögű háromszögek száma $H (n)$ legyen. Mivel $n$ pont $T (n) = (\binom{n}{3})$ háromszöget határoz meg, az összes háromszögek legfeljebb $h (n) = \frac{H (n)}{T (n)}$ része lehet hegyesszögű. Feladatunk állítása ezzel a jelöléssel a

\begin{matrix} h (100) \leq 0, 7 \end{matrix}

(1)

egyenlőtlenséget jelenti, ezt fogjuk bizonyítani. Ennek érdekében először azt mutatjuk meg, hogy

h (n)

n

növelésével monoton csökken.
Vegyünk fel tetszőlegesen

(n + 1)

pontot és jelöljük az általuk meghatározott hegyesszögű háromszögek számát

K (n + 1)

-gyel. (Az előbb definiált

H (n + 1)

az ilyen konkrét

K (n + 1)

-számok között a legnagyobbik, ha az

(n + 1)

pontot minden lehetséges módon felvesszük.) Tegyük fel, hogy a pontok sorszámozva vannak, és hagyjuk el közülük az elsőt. A visszamaradó

n

pont által meghatározott hegyesszögű háromszögek számát jelöljük

K_{1} (n)

-nel. Hasonló módon jelöljük

K_{j} (n)

-nel a

j

-ik pont elhagyása után visszamaradó

n

pont által meghatározott hegyesszögű háromszögek számát. Az

\begin{matrix} S_{n} = K_{1} (n) + K_{2} (n) + ... + K_{n + 1} (n) \end{matrix}

(2)

összegben az eredeti

(n + 1)

pont által meghatározott hegyesszögű háromszögek száma szerepel, de minden ilyen háromszöget többször vettünk számításba. Egy adott hegyesszögű háromszög ugyanis csak akkor nem szerepel

K_{j} (n)

-ben, ha a

j

-ik pont az illető háromszögnek csúcsa. Ez a háromszög tehát a (2) összeg 3 tagjában nem szerepel, vagyis

(n - 2)

tagjában szerepel. Emiatt

S_{n}

a hegyesszögű háromszögek számának

(n - 2)

-szerese, azaz

\begin{matrix} S_{n} = (n - 2) \cdot K (n + 1) . \end{matrix}

(3)

Említettük már, hogy

K (n + 1) \leq H (n + 1)

, és hasonlóan

K_{j} (n) \leq H (n)

. Emiatt a (2) összeg bármelyik tagja nem nagyobb, mint

H (n)

, és így

\begin{matrix} S_{n} \leq (n + 1) \cdot H (n), \end{matrix}

ahonnan (3) alapján a

\begin{matrix} K (n + 1) \leq \frac{n + 1}{n - 2} H (n) \end{matrix}

egyenlőtlenséget kapjuk. Mivel ez tetszőleges

(n + 1)

pontra érvényes, teljesül ez az egyenlőtlenség, a

K (n + 1)

számok legnagyobbikára,

H (n + 1)

-re is:

\begin{matrix} H (n + 1) \leq \frac{n + 1}{n - 2} \cdot H (n) . \end{matrix}

(4)

Behelyettesítve

H

helyére a

h

-val kifejezett értékét, a kívánt egyenlőtlenséget kapjuk:

\begin{matrix} h (n + 1) \cdot (\binom{n + 1}{3}) \leq \frac{n + 1}{n - 2} \cdot h (n) \cdot (\binom{n}{3}) \\ \frac{1}{6} h (n + 1) \cdot {(n + 1) n (n - 1) (n - 2)} \leq \frac{1}{6} (n + 1) \cdot h (n) \cdot {n (n - 1) (n - 2)}, \\ h (n + 1) \leq h (n), \end{matrix}

h (n)

tehát valóban monoton csökken.
Mármost ahhoz, hogy (1)-et bebizonyítsuk, elegendő olyan

n \leq 100

számot találni, melyre

\begin{matrix} h (n) \leq 0, 7, \end{matrix}

(5)

hiszen

h (n)

monoton volta miatt (5)-ből következik (1).
Ha

n = 3

, akkor

h (3) = 1

, ez még túl nagy.
Ha

n = 4

, akkor

H (4) < 4

, mert nem lehet négy pontot úgy megadni, hogy az általuk meghatározott háromszögek mind hegyesszögűek legyenek. Ha ugyanis a négy pont konvex burka négyszög (az ábra a) része), e négyszög négy csúcsában levő szögei nem lehetnek mind hegyesszögek (összegük

360^{\circ}

), van köztük derékszög vagy tompaszög, ennek a csúcsát és a négyszög vele szomszédos másik két csúcsát véve, derékszögű vagy tompaszögű háromszöget kapunk.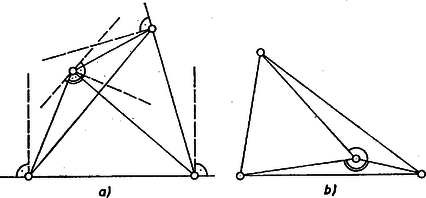

Ha pedig a négyszög konvex burka háromszög, vegyük e konvex burok oldalaihoz harmadik csúcsnak a negyedik pontot, amelyik a háromszög belsejében van (az ábra b) része). E három háromszögnek a belső pontra támaszkodó szögeinek összege

360^{\circ}

, köztük van tompaszög, vagyis a megfelelő háromszög tompaszögű háromszög. Ezzel beláttuk, hogy

H (4) < 4

. Viszont az ábra a) része olyan esetet mutat, amikor

K (4) = 3

, tehát

H (4) = 3

h (4) = 0, 75

, és ez még mindig nagyobb, mint

0, 7

.
Ha

n = 5

, akkor (4) szerint

H (5) \leq \frac{5}{2} H (4) = 7, 5

, viszont

H (5)

egész szám, tehát

H (5) \leq 7

, és

h (5) \leq 0, 7

. Ezzel (5)-öt beláttuk az

n = 5

értékre, amivel feladatunk állítását a fentebbiek szerint bebizonyítottuk.

Komjáth Péter