Kezdőlap


Feladat:	Pontversenyen kívüli P.72	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bacsó Gábor , Donga György , Ferró József , Göndőcs Ferenc , Papp Zoltán
Füzet:	1973/április, 167 - 169. oldal		PDF \| MathML
Témakör(ök):	Tengely körüli forgatás, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Körök, Térgeometriai bizonyítások, Tetraéderek, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/május: Pontversenyen kívüli P.72

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Legyen az $A B C D$ tetraéder tetszőleges belső pontja $P$ . Ennek "belső'' voltából következik, hogy ha a $B C$ egyenessel határolt $B C D$ félsíkot $B C$ mint tengely körül úgy fordítjuk bele a $B C A$ (alap-) síkba, hogy $D$ a $B C$ -nek $A$ -t tartalmazó partjára jusson, akkor az elfordulás közben a félsík áthalad $P$ -n (és sorra áthalad a $D A$ szakasz pontjain).

1. ábra

Jelöljük a

B C P

félsík és a

D A

szakasz közös pontját

P_{a}

-val, és tekintsük a

P

közös csúccsal és

P P_{a}

közös éllel bíró

P P_{a} A B

és

P P_{a} D C

triédereket (1. ábra).
Alkalmazzuk rájuk azt a tételt, hogy konvex triéder bármelyik két oldalának (más szóval élszögének) összege nagyobb, mint a harmadik oldala (e segédtételt utólag bebizonyítjuk):

\begin{matrix} P_{a} P A ∢ + A P B ∢ > P_{a} P B ∢, \\ P_{a} P D ∢ + D P C ∢ > P_{a} P C ∢ . \end{matrix}

Adjuk össze ezeket és a

\begin{matrix} C P B ∢ = D P C ∢ \end{matrix}

egyenlőséget és vegyük figyelembe, hogy a bal oldali első szögek egy síkban vannak, ugyanúgy a jobb oldalon álló három szög is és hogy

P

B C P_{a}

háromszögnek belső pontja:

\begin{matrix} A P D ∢ + D P C ∢ + C P B ∢ + B P A ∢ > 360^{\circ} . \end{matrix}

(1)

Ismételjük meg végzett meggondolásunkat még kétszer, az

A

B

C

betűk helyére rendre előbb

B

C

A

-t, majd

C

A

B

-t írva, és felhasználva, hogy

P

abban a

180^{\circ}

-nál kisebb lapszögtartományban is benne van, melynek éle a

C A

egyenes, szárlapjai a

C A B

és

C A D

félsíkok (vagyis amely tartományban tetraéderünk is benne van), valamint hogy

P

A B

élű

180^{\circ}

-nál kisebb

C (A B) D

lapszögtartományra nézve is belső pont. Így felírhatjuk (1)-et a mondott betű-változásokkal:

\begin{matrix} B P D ∢ + D P A ∢ + A P C ∢ + C P B ∢ > 360^{\circ}, & (1') \\ C P D ∢ + D P B ∢ + B P A ∢ + A P C ∢ > 360^{\circ} . & (1'') \end{matrix}

E három egyenlőtlenséget összeadva, a bal oldalon tetraéderünk mind a hat élének

P

-ből vett látószöge kétszer szerepel és a jobb oldalon

1080^{\circ}

is kétszerese az állításbeli szögnek, tehát az összeadás eredményét felezve a bizonyítandó állítást kapjuk (más tag ugyanis nincs).
2. A fölhasznált segédtételt a

P

csúccsal és a belőle kiinduló

e

f

g

félegyenesekkel meghatározott konvex triéderre bizonyítjuk, e

3

félegyenes tehát nincs egy síkban (2. ábra).

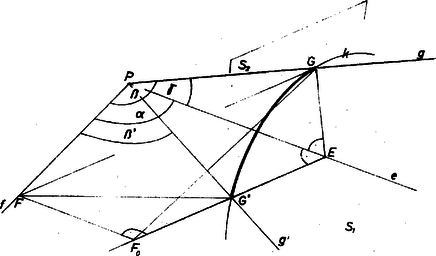2. ábra

A triédernek az

e

f

élpár közti oldalát (a mértékszámát)

α

-val jelöljük, az

f

g

és a

g

e

oldalát

β

-val,

γ

-val, a jelölést úgy választva, hogy

180^{\circ} > α ≧ β ≧ γ (> 0^{\circ})

legyen. Ekkor elegendő az

\begin{matrix} α < β + γ \end{matrix}

(2)

egyenlőtlenséget bizonyítanunk (

β < γ + α

és

γ < α + β

nyilvánvalóan teljesül; sőt (2)-t is csak az

a > β ≧ γ

nagyságviszony esetére kell, hiszen

α = β

esetén nyilvánvalóan fennáll).
Forgassuk bele

g

-t

e

körül

e

és

f

-nek

S_{1}

síkjába, így

γ < α

miatt

g

e

f

szögtartományba jut a

g'

helyzetbe; ekkor

e

és

g'

szöge

γ

. Jelöljük

g'

és

f

szögét

β'

-vel, így (2) céljára a

β' < β

egyenlőtlenséget kell bizonyítanunk. Vegyük föl

f

-en a

F

g

-n a

G

pontot úgy, hogy

P F = P G

legyen, és jelöljük

G

új helyzetét

g'

-n

G'

-vel; így feladatunk a közös szárú

G P F

és

G' P F

egyenlő szárú háromszögekre tekintettel

F G' < F G

bizonyítására módosul.
A forgatás közben

G

egy

k

kör

G G'

ívét írja le, legyen

k

középpontja (az

e

tengelyen)

E

. A kör

S_{2}

síkja merőleges

e

-re, ezért az

e

f

által meghatározott

S_{1}

síkra is, így

F

-nek

S_{2}

-n levő

F_{0}

vetületét a két sík

E G'

metszésvonalán kapjuk. Pontosabban:

F_{0}

E G'

félegyenes pontja, mert

γ < α < 180^{\circ}

és

F F_{0} | | e

miatt

F_{0}

azon a partján van

e

-nek, mint

G'

. Így a

k

-nak

F_{0}

-hoz legközelebbi pontja

G'

, tehát

F_{0} G' < F_{0} G

, végül a közös befogójú

F F_{0} G'

és

F F_{0} G

derékszögű háromszögekből

F G' < F G

, amit bizonyítani akartunk.

Megjegyzések. 1. Az (1) egyenlőtlenségbeli eredményünket kimondhatjuk így: Az

A B C D

térbeli négyszög (torznégyszög) egymás utáni

A B

B C

C D

D A

oldalaihoz és a négyszög konvex burkában levő

P

ponthoz tartozó négy látószög összege nagyobb

360^{\circ}

-nál, vagyis a síkbeli négyszög négy oldalához és egy belső pontjához tartozó négy látószög összegénél.
2. Kissé más, önmagában szintén érdekes eredményt kapunk az alábbiak szerint. Messe a

C P

félegyenes az

A B D

lap síkját

P^{*}

-ban (1. ábra, a

B P_{a}

szakaszon), alkalmazzuk segédtételünket a

P

közös csúcsú,

P P_{a}

közös élű

P P_{a} A P^{*}

és

P P_{a} B D

triéderekre és képezzük a két egyenlőtlenség összegét:

\begin{matrix} P_{a} P P^{*} ∢ + P_{a} P A ∢ > P^{*} P A, \\ D P B ∢ + D P P_{a} ∢ > P_{a} P B ∢ = P_{a} P P^{*} ∢ + P^{*} P B ∢, \end{matrix}

amiből

\begin{matrix} D P A ∢ + D P B ∢ > P^{*} P A ∢ + P^{*} P B ∢ . \end{matrix}

Megfogalmazását az olvasóra hagyjuk. Erre is építhető a feladat állításának egy bizonyítása.
3. A feladatban szereplő

6

szög összege tetszőlegesen közel lehet

540^{\circ}

-hoz, ha közülük három közel van

0^{\circ}

-hoz, három pedig

180^{\circ}

-hoz, ami bekövetkezhet, ha például

P

és

D

"nagyon messze'' vannak az

A

B

C

pontoktól, egymáshoz viszont "közel'' vannak.
4. Segédtételünk kimondható így is: a háromszög egyenlőtlenség konvex gömbháromszögekre is érvényes. Ehhez (2)-ből így jutunk. Messe a

P

körüli egységnyi sugarú gömb a triéder

e

f

g

élét rendre az

E^{*}

F^{*}

G^{*}

pontban; így a triéder lapsíkjait a

P

körüli

F^{*} G^{*}

G^{*} E^{*}

E^{*} F^{*}

körívekben metszi. Ezek egyrészt a gömbünkön levő

E^{*} F^{*} G^{*}

gömbháromszög oldalai, másrészt hosszuk rendre egyenlő az

α

β

γ

szög radiánban vett mértékszámával, tehát (2)-ben ezt kaptuk:

\hat{E^{*} F^{*}} < \hat{F^{*} G^{*}} + \hat{G^{*} E^{*}}

, hacsak mindhárom oldal kisebb, mint

π

(ill.

180^{\circ}

).
5. A fölhasznált segédtételre egy más bizonyítást adtunk az 1646. feladat II. megoldásához fűzött megjegyzésben.^{$^{*}$}

^{$^{*}$}K.M.L. 41 (1970) 112. old.