I. Ha nem volna kikötve, hogy a pontok ne lehessenek egy egyenesen, akkor pl. a számegyenes összes racionális koordinátájú pontja eleget tenne a feladat első követelményének. Így természetesnek tűnik, hogy ‐ amennyiben egyáltalán teljesíthető a követelmény ‐ legkönnyebben olyan ponthalmazt konstruálhatunk, amelynek pontjai egynek a kivételével egy egyenesen vannak.
Próbáljuk ezért az egyenes szerepére a koordináta-rendszer $x$ tengelyét venni, külső pontnak pedig a $P_0\left(0;1\right)$ pontot. Ha még a $P_k\left(k=\mathrm{1,}\mathrm{2,}\text{...}\right)$ pontokat úgy adjuk meg, hogy minden $k$-ra $P_k=\left({\pm }_k\mathrm{,}0\right)$ és $x_k$ racionális, akkor csak arra kell ügyelnünk, hogy a $P_0{P}_k$ távolság minden $k$-ra racionális legyen.
Legyen a $P\left(x\mathrm{,}0\right)$ pont olyan, hogy $x$ racionális, azaz $x=r/s$, ahol $r$ és $s$ egész szám, $s\ne 0$. A $P_{0}P$ távolság Pitagorasz tétele szerint

(0;1/2) középpontú, $1/2$ sugarú kör. Megmutatjuk, hogy a $P{\text{'}}_i$ és $P{\text{'}}_j$ inverz pontok $P{\text{'}}_{i}P{\text{'}}_j$ távolsága is racionális. A $P_0{P}_i{P}_j$ és $P_{0}P\text{'}P{\text{'}}_i$ háromszögek ugyanis hasonlóak, mert $P_0$-nál levő szögük közös, és (1. ábra):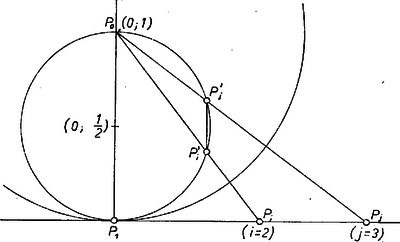

 

 

1. ábra

 

$\begin{array}{c}{\displaystyle \frac{P_0{P}_i}{P_0{P}_j}=\frac{P_{0}P{\text{'}}_j}{P_{0}P{\text{'}}_i}\mathrm{,}}\end{array}$

hiszen az inverzió definíciója szerint $\overline{P_0{P}_i}\cdot \overline{P_{0}P{\text{'}}_i}=\overline{P_0{P}_j}\cdot \overline{P_{0}P{\text{'}}_j}=1$. Az utóbbi egyenlőségből az is következik, hogy $P_{0}P{\text{'}}_i$ és $P_{0}P{\text{'}}_j$ is racionális, hiszen ezek a racionális $P_0{P}_i$, $P_0{P}_j$ távolságok reciprokával egyenlőek. A hasonlóság miatt

$\begin{array}{c}{\displaystyle P{\text{'}}_{i}P{\text{'}}_j=\frac{P_{0}P{\text{'}}_i}{P_0{P}_i}\cdot P_i{P}_j=\frac{P_i{P}_j}{P_0{P}_i^2}\mathrm{,}}\end{array}$

tehát $P{\text{'}}_{i}P{\text{'}}_j$ is racionális.
Ezek szerint a $P_i$ pontok $\left(i>0\right)$ invertálásával sikerült olyan pontokat megadni, melyek egy körön vannak, tehát köztük nincs három egy egyenesen, és közülük bármelyik kettő távolsága racionális. ‐ Azt is látjuk, hogy a $P$ pontokhoz $P_0$ -t is hozzávehetjük, hiszen $P_{0}P{\text{'}}_i$ is racionális.

 

Komjáth Péter, Göndőcs Ferenc

 

II. megoldás. A feladat két részét egy csapásra oldjuk meg, ha megadunk végtelen sok pontot egy körön úgy, hogy közülük bármely két pont távolsága racionális.
Induljunk ki az egységsugarú kör egy $P_0$ pontjából, és forgassuk el a pontot rendre $\alpha \mathrm{,}2\alpha \mathrm{,}\text{...}\mathrm{,}n\alpha \mathrm{,}\text{...}$ szöggel. A kapott pontokat jelöljük $P_1\mathrm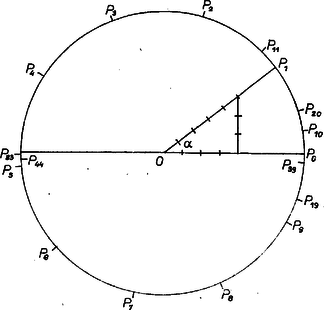{,}{P}_2\mathrm{,}\text{...}\mathrm{,}{P}_n\mathrm{,}\text{...}$-nel (2. ábra).

 

 

2. ábra

 

Nézzük meg, mi a feltétele annak, hogy így végtelen sok különböző pontot kapjunk. Nyilvánvaló, hogy akkor és csak akkor kapunk végtelen sok különböző pontot, ha nincs olyan $n$ és $k$ egész szám, amelyre $n\alpha =k\cdot \pi$ teljesül.

Következésképpen ha nincs olyan $n$, melyre $\text{sin}n\alpha =0$ lenne, akkor valóban végtelen sok különböző pontot kapunk, $n$-et minden határon túl növelve.
Elegendő azt biztosítani, hogy a $P_0{P}_n$ távolság racionális legyen minden természete $n$-re, hiszen ha $k<l$, akkor a $P_k{P}_l$ távolság egyenlő a $P_0{P}_n$ távolsággal, ha $n=l-k$. Jelöljük az $O{P}_0{P}_n$ háromszög $O$-nál levő szögét $\omega$-val, akkor

$\begin{array}{c}{\displaystyle P_0{P}_n=2\text{sin}\frac{\omega }{2}=2\left|\text{sin}\frac{n\alpha }{2}\right|\mathrm{,}}\end{array}$

hiszen $\left(n\alpha -\omega \right)$ vagy $\left(n\alpha +\omega \right)$ a $2\pi$-nek egész számú többszöröse. Jelöljük $\alpha /2$-t $\beta$-val, így olyan $\beta$ kell keresnünk, melyre $\text{sin}n\beta$ racionális minden $n$ természetes számra. Ismeretes, hogy $\text{sin}l\beta$ megadható $\text{sin}\beta$ és $\text{cos}\beta$ polinomjaként. Nevezetesen

$\begin{array}{c}{\displaystyle \text{sin}l\beta =\text{sin}\beta \left(2^{l-1}{\text{cos}}^{l-1}\beta +a_1{\text{cos}}^{l-3}\beta +a_2{\text{cos}}^{l-5}\beta +a_3{\text{cos}}^{l-7}\beta +\text{...}\right)\mathrm{,}}\end{array}$

(1)

ahol $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}$ egész számok.^{${}^{*}$} Ha tehát $\text{sin}\beta$ és $\text{cos}\beta$ racionális, akkor $\text{sin}l\beta$ is racionális minden $l=\mathrm{1,}\mathrm{2,}\text{...}$ számra.
Tekintsünk egy olyan derékszögű háromszöget, melynek egyik hegyesszöge $\beta$. Ha a háromszög oldalai $a$, $b$ és $c$ egészek, akkor mind $\text{sin}\beta$ mind $\text{cos}\beta$ racionális. Tegyük fel, hogy $a$ és $c$ relatív prímek, azaz legnagyobb közös osztójuk $1$. Ekkor $\text{cos}\beta =a/c$ és legyen $c$ a $2$-től különböző. (Ilyen háromszög van, pl. $a=3$, $b=4$, $c=5$.)
Megmutatjuk, hogy a fenti feltételeket kielégítő $\beta$-kra $\text{sin}l\beta \ne 0$, minden $l$-re. (Ebből következik, hogy $\text{sin}l\alpha =0$ sem következik be semmilyen $l$-re.) (1)-ből átrendezéssel és $c^{l-1}$-nel való beszorzással adódik

$\begin{array}{c}{\displaystyle \frac{\text{sin}l\beta }{\text{sin}\beta }\cdot c^{l-1}-c^{l-1}\cdot 2^{l-1}{\text{cos}}^{l-1}\beta =a_1{c}^{l-1}{\text{cos}}^{l-3}\beta +a_2{c}^{l-1}{\text{cos}}^{l-5}\beta +\text{...}}\end{array}$

Ha $\text{sin}l\beta =0$ lenne valamely $l$-re, akkor a bal oldal értéke

$\begin{array}{c}{\displaystyle c^{l-1}\cdot 2^{l-1}\cdot {\left(\frac{a}{c}\right)}^{l-1}={\left(2a\right)}^{l-1}}\end{array}$

lenne, míg a jobb oldalon egy, a $c^{l-1}$-nel osztható szám állna, hiszen

$\begin{array}{c}{\displaystyle a_k{c}^{l-1}{\text{cos}}^{l-2k-1}\beta =a_k{c}^{l-1}\cdot {\left(\frac{a}{c}\right)}^{l-2k-1}=a_k{a}^{l-2k-1}{c}^{2k}\mathrm{.}}\end{array}$

Mivel $a$ és $c$ relatív prímek, ez ellentmondás. Tehát $\text{sin}l\beta$ semmilyen $l$-re nem nulla, amint állítottuk.

 

Ferró József, Papp Zoltán

---

^{${}^{*}$}Lásd p1. 1575. feladat, K. M. L. 37 (1968) 120. o.