Feladat: Pontversenyen kívüli P.68 Korcsoport: - Nehézségi fok: nehéz
Megoldó(k):  Göndőcs Ferenc ,  Komjáth Péter ,  Reviczky János ,  Szabó György 
Füzet: 1973/november, 149 - 153. oldal  PDF  |  MathML 
Témakör(ök): Gráfok összefüggősége, Euler-féle poliédertétel alkalmazásai, Kocka, Szabályos testek, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1970/április: Pontversenyen kívüli P.68

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A kockamodell minden egyes összefüggő kiterítése 6 egymáshoz csatlakozó négyzet, 5 él hajtogatható, a többi 7 van felvágva. A 3 élirány mindegyike képviselve van e vágásokban, mert ha pl. a 4 függőleges él egyike sem lenne felvágva, akkor a 7 vágott élből 4 esnék vagy az alaplap, vagy a fedőlap kerületére és azt a lapot elvágná a többiektől (másrészt pedig a 4 oldallap legföljebb kétrétűen lenne lelapítható a síkba). Ez azt is jelenti, hogy minden lapnak legföljebb 3 élét vághatjuk fel.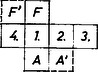
a) Ha van olyan élirány, amelyikkel párhuzamos 4 él közül csak 1-et vágtunk fel, akkor tartsuk ezt függőlegesen. Minden ilyen kiterítésben a 4 oldallap egymás után csatlakozik egy 4×1-es téglalappá, a további 6 vágásból 3‐3 az alap-, illetve a fedőlapot teszi hajtogathatóvá, ezek a téglalap egyik egyik hosszabb oldalán csatlakoznak a palást-téglalaphoz. Megjegyezzük csupán, hogy erre a lényegesen különböző ‐ azaz tükrözéssel, forgatással egymásba át nem vihető ‐ lehetőségek száma 6: ha az F fedőlap az 1. ábra F' helyzetében van, akkor az A alaplap az alsó élen 4-féleképpen csatlakozhat, az F helyzetben pedig 2 módon: A-ban és A'-ben; a lehetőségek száma egyébként nem lényeges az állítás szempontjából.

 

 

1. ábra
 

Az ilyen esetekben az oktaédernek 4 éle vízszintes, közülük az előírás szerint 3-at vágunk fel; a modellje már evvel szétnyílik két négy oldalú gúla palásttá (2. ábra).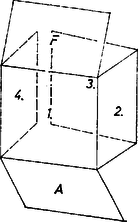
 

 

2. ábra
 

E két paláston viszont csak 1‐1 oldalélt vágunk fel, így a két gúlapalást 4‐4 háromszöglapja külön-külön összefüggő marad és kiteríthető, továbbá e két palást egymással is összefügg a nem vágott vízszintes él mentén és kiteríthető. Az 1. ábrabeli kiterítés megfelelője a 2a. ábrán látható.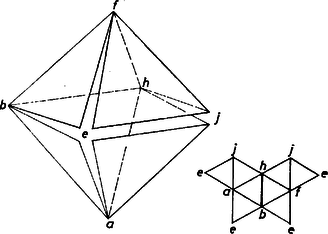
 

 

2a. ábra
 

Az ide tartozó esetekben tehát igazoltuk a feladat állítását.
b) A kockamodell hátralevő felvágási lehetőségeiben mindhárom éliránnyal párhuzamosan legalább 2 élt vágunk fel. A 7 vágás egyetlen lehetséges ilyen eloszlása 3+2+2. Vágjunk fel a függőleges élekből 3-at, vagyis csak 2 oldallapot hagyunk egymással közvetlen kapcsolatban ‐ ezeket tekintjük a kiterítés magjának ‐, ezekhez közvetlenül csak A és F csatlakozhat, és legalább az egyik csatlakozik is, a további 2 oldallap pedig A és F valamelyikén át csatlakozik.
Legyen mindvégig a kocka (hajtogatva) együtt maradó két oldallapja az 1. ábra 1-es és 2-es lapja ‐ mondjuk így is: elülső és jobb oldali lapja. Az oktaédermodell innen adódó felvágásai céljára leírjuk egy az a) részben már látott felvágását. Fordítsuk úgy a 2. ábra modelljét, hogy elülső csúcsa fölülre és jobb oldali csúcsa előre jusson (3. ábra), így a felső gúla a, b, c, d lapjai virágsziromszerűen szétnyílnak és mind a 4 vízszintes él hajtogatott.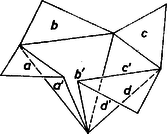
 

 

3. ábra
 

Ebből származtatjuk a hátralevő kockafelvágásoknak megfelelő oktaéderfelvágásokat úgy, hogy bizonyos lapokat levágunk és valamelyik szomszédjukra átragasztjuk őket. Az 1-es, 2-es hajtogatás miatt d mindenesetre levágandó lesz d'-ről, a többi 3 alsó‐felső lappár viszont mindig együtt marad, a az a'-vel, b a b'-vel, c a c'-vel.
b 1. Tekintsük először a kockának azokat a felvágásait, amelyekben az 1, 2 maghoz A és F közül csak az egyik csatlakozik. Az 1, 2 mag szimmetrikus egyrészt a vízszintes felező síkra, másrészt a közös élükön átmenő átlós síkra, ezért elég azt vennünk, ha a maghoz csatlakozó lap A, és ha ez az 1-es alá csatlakozik. Ezzel (a 3 oldalélen túl) további 3 élt vágtunk fel: 2 fedőélt, valamint a 2-es és A lapok közti élt (a 4. ábrán az eddigi 6 vágott él vastagítva van), közülük 2 elölről hátra fut, ezért a 4-es (bal oldal-) lap ezekkel párhuzamos élei már nem vághatók, tehát a 4-eshez két párhuzamos oldalán csatlakozik 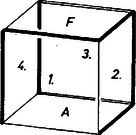A és F.
 

 

4. ábra
 

A hetediknek felvágandó él a 3-as (hátulsó) lapot választja majd el vagy A-tól, vagy F-től (az ábra kettős vonalú élei), tehát a befejezésre itt 2 lehetőség van.
Felsoroljuk a 3. ábra virágján végzendő változtatásokat. A két felvágott fedőél miatt a d'-ről levágott d mindjárt hozzáragasztandó a-hoz, majd d-hez a c lap is (a jobb oldali oktaédercsúcs körüli 4 lap így d, c, c', d' sorrendben összefüggő és kiteríthető), továbbá az A-4-F összefüggés miatt a' és b' közé vágás jön, de kapcsolatuk megmarad az a', a, d, c, c', b' lapsorozaton át (5. ábra).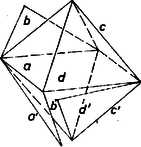
 

 

5. ábra
 

Nincs szükség más változtatásra, ha a 3-as lap az F-en át csatlakozik a maghoz; ha viszont ezt elvágjuk, emiatt b és c összeragasztandók, de ekkor a 3-as és A közti csatlakozás miatt a b' és c' közös élét kell vágnunk, megmarad a hátsó csúcs kiteríthetősége és összefüggősége.
b 2. Ha végül az 1, 2 maghoz A-t F-et is hajtogatással csatlakoztatjuk, mégpedig A-t ismét az 1-es laphoz, akkor F-et csak a 2-eshez lehet, különben az oldalkapcsolataitól elvágott 3-assal a 3-F-1-A lapnégyes jönne létre, amit már láttunk az a) esetekben. Ezzel elvágtuk A-t a 2-estől és F-et az 1-estől (6. ábra bal oldali része), és a hátralevő 2 vágás egyike a 3-ast, másika a 4-est vágja majd el A-tól vagy F-t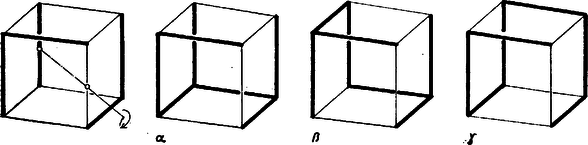ől.
 

 

6. ábra
 

Látható, hogy az eddig felvágott 5 él együttese önmagába megy át a kockának azzal a 180∘-os elfordításával, mely az 1-es és 2-es lapot egymással fölcseréli, ezért a hátralevő 2 vágási él gondolható 2⋅2=4 megválasztási lehetősége közül kettő lényegében azonos. Elég tehát bizonyítanunk a feladat állítását a következő 3 esetben (6. ábra azonos jelű részei):
α) a 3-as lap is, a 4-es is F-en át csatlakozik a maghoz;
β) a 3-as az F-hez, a 4-es az A-hoz csatlakozik;
γ) a 4-es az F-hez, a 3-as az A-hoz csatlakozik.
Az oktaéder megfelelő felvágásai a sziromalakzat következő származékai lesznek: d-t mindhárom esetben levágjuk d'-ről és átragasztjuk a-hoz, az α) esetben nincs is más alakítani való,
a β) esetben elvágjuk b'-t a'-től, viszont hozzáragasztjuk b-t a-hoz;
a γ) esetben elvágjuk b'-t c'-től, viszont hozzáragasztjuk b-t c-hez.
A b 1. esetben leírtakhoz hasonlóan az oktaédermodell mindig kiteríthető és összefüggő marad.
Sorra vettük a kocka felvágásának minden lehetőségét, mindegyikben igaznak találtuk a feladat állítását; a bizonyítást tehát befejeztük. ‐ Azt is kaptuk, hogy a kocka lényegesen különböző hálózatainak száma 6+2+3=11.
 

II. megoldás. 1. Először a fölvágott modellnek a föltevésből következő tulajdonságait állapítjuk meg. A modell 12 éléből 7-et fölvágva, 5 éle hajtogathatóan marad. A hálózatnak a síkra kiterített állapotában mindegyik ilyen él két oldalán álló lap középpontjait összekötve, egy 5 élű, 6 csúcsú HI, gráfot kapunk, csúcsai a 6 kockalap középpontjai. (A H betűvel a hatlapú szabályos testre kívánunk utalni.) A hálózat összefüggősége azt jelenti, hogy bármelyik lapközéppontból bármelyik másikba át lehet menni HI élei mentén. Ezért HI-et a kocka lapközéppont‐összefüggési gráfjának nevezzük.
A hálózatnak mint sokszögnek a határvonalait tekintve, a 6 lap együttes kerülete 24 egységnyi (kockaélnyi). Ebből az 5 hajtogatott él 5⋅2=10 egységnyit vesz föl belső osztóvonalakra, a maradó 14 egységnyi pedig a 7 vágott élből ered, mindegyik 2 helyen jelenik meg, ezek határolják a hálózatot. Belső határvonal nem lehet a sokszögben, mert ha volna benne a hálózathoz nem tartozó rész: ,,lyuk'', ennek szögei derékszögek lennének, oldalai egységnyiek vagy ennek többszörösei, területe egy vagy több kockalapnyi, márpedig egyetlen négyzet körülzárásához is 8 vele egybevágó négyzet szükséges, több, mint ahány lapja a kockának van. Így ‐ az összefüggőség alapján egyetlen határvonal van, ezen bármely pontjából indulva és visszafordulás nélkül haladva, 14 egységnyi út után visszaérünk a kiindulópontba.
Másrészt a hálózat síkba kiteríthető volta alapján minden egyes kockacsúcsba befutó 3 él közül legalább 1 fel van vágva, különben nem szűnnék meg a csúcsba befutó 3 lap egymáshoz képest merevített, térbeli helyzete.
Egybevetve az utóbbiakat, kapjuk, hogy a hálózat kerületét egységszakaszokra bontó 14 pont közt a kockának mind a 8 csúcsa legalább 1-szer előfordul, tehát bármelyik kockacsúcsból bármelyik másikba eljuthatunk felvágott élek mentén haladva. És ez természetesen akkor is érvényes, ha a hálózatot visszahajtogatjuk kockává, vagy még fel sem vágtuk, csak alkalmasan kijelöltük a felvágandó éleket. Eszerint, a modell felületén a 8 csúcsot és a felvágásra kijelölt 7 élt egy HII gráf szögpontjainak, illetőleg éleinek tekintve, ezt joggal nevezhetjük a kocka felvágási gráfjának is és a kockacsúcsok bejárási, összefüggési gráfjának is.
A továbbiakban HI-et is a hálózatból visszaállított kockamodellen tekintjük.
2. A kívánt bizonyítás más oldalról való előkészítéséül bizonyítás nélkül kimondjuk a kockánk és oktaédereink kölcsönös helyzetéből adódó alábbi kapcsolatokat; bizonyításuk átgondolását az olvasóra hagyjuk.
Kockánk O középpontja egyszersmind oktaéderünknek is középpontja.
Bármely az O-ból induló félegyenes mindkét poliéder határfelületét egy-egy pontban metszi; más szóval: e két pont egymás vetülete a másik poliéderen, O-ból való centrális vetítés mellett.
Amint a kocka lapközéppontjainak az oktaéderen levő vetületei az utóbbinak a csúcsai (hiszen rendre azonosak), hasonlóan az oktaéder lapközéppontjainak a kockán levő vetületei a kocka csúcsai.
Az oktaéder egy élének a kockán levő vetülete olyan két egyenesszakaszból álló törött vonal, mely a kocka két szomszédos lapjának középpontját köti össze, a köztük levő él felezőpontjában megtörve.
A kocka egy élének az oktaéderen levő vetülete olyan két egyenesszakaszból álló törött vonal, mely az oktaéder két szomszédos lapjának középpontját köti össze, a köztük levő él felezőpontjában megtörve.
3. Tekintsük mármost az oktaédermodell 6 csúcsát, valamint az előírás szerint felvágandó 5 élét egy NI gráf szögpontjainak, illetve éleinek (az N betűvel a nyolclapú szabályos testre utalunk) és nevezzük az oktaéder felvágási gráfjának.
Az előírás szerint NI és a kockalapközéppontok HI összefüggési gráfja egymás vetületei. Mivel HI szögpontjai közt szerepel a kocka összes lapközéppontja, azért NI, szögpontjai közt szerepel az oktaéder összes csúcsa. Eszerint az oktaédermodell mindegyik csúcsába befutó élek közül legalább 1 fel van vágva, vagyis mindegyik csúcsába befutó 4 lap ‐ ha a többi 4 laptól eltekintünk ‐ síkba kiteríthető.
Ahhoz, hogy a 8 oktaéderlap együttese is kiteríthető, még egy megállapítást teszünk. Az NI gráf 5 élét egyenként tekintve, 10 végződésük eloszlik az oktaéder 6 csúcsára és mindegyikbe legalább 1 végződés fut be. Ezért 1-nél több befutás legföljebb 10-6=4 csúcsban lehet, és továbbmenve legalább 6-4=2 csúcsba csak 1 végződés fut be (mint egy zsákutca). Kezdjük az oktaéderlapok kiterítését az NI-nek egyik ilyen végpontja, a C1 körüli 4 lappal. Már csak arra hivatkozunk, hogy HI összefüggő volta alapján NI is összefüggő (a vetítés megtartja az összefüggőséget), ennek alapján C1 környezete után kiteríthető az NI-beli C2 szomszédjának környezete és így tovább, az oktaéder mindegyik csúcsának környezete, vagyis a felvágott modell egésze.
Meg kell azonban mutatnunk, hogy az ilyen kiterítés összefüggő, hiszen NI-en haladva a fentiek szerint eljutunk 1-nél több élű szögpontjába, ekkor a megfelelő csúcsba befutó élek közül legalább 2 van felvágva, és ezért a csúcs körüli 4 lap közt van olyan kettő, amelyek csak a további 4 lapon át függnek össze egymással. Tekintsük evégett a fenti HII (kockacsúcs-összefüggési) gráfnak az oktaéderen levő vetületét is egy NII gráfnak. Ennek szögpontjai tehát a 8 lapközéppont és mindegyik éle olyan két szomszédos lap középpontját köti össze (közös élük felezőpontján át), amelyek közti oktaéderél nincs felvágva, hiszen a neki megfelelő kockaél ‐ mint HII-nek éle ‐ fel van vágva. És mivel HII összefüggő, azért NII is, és NII mentén az oktaédermodell kiterítettje is összefüggő. A probléma állítását ezzel bebizonyítottuk.
 

Összeállítva Göndőcs Ferenc, Komjáth Péter és Szabó György dolgozataiból.
 

Megjegyzések. 1. Tulajdonképpen azt is bebizonyítottuk a fentiekkel, hogy fordítva, minden kiteríthető és összefüggő oktaéderhálózathoz is tartozik egy kiteríthető és összefüggő kockahálózat. Így ‐ az I. megoldást is figyelembe véve ‐ a különböző kockahálózatok és különböző oktaéder hálózatok száma egyaránt 11.
2. Felhasználható a bizonyítás befejezésében az is, hogy gráfjainkban nincs ún. körút, vagyis olyan részük, amelyen egy szögpontból egy másikba olyan két úton lehetne eljutni, melyek egyetlen élt sem tartalmaznak közösen. HII-re ez így adódik: ha volna benne körút, ez elvágná egymástól a kocka felületének azt a két részét, amely jobb és bal kezünk felől esnék, míg a körutat egyszer körüljárjuk, így pedig a kiterítés nem lenne összefüggő. N1 pedig azért körútmentes, mert ha a fentiek szerinti ,,zsákutca''-éleit elhagyjuk, legföljebb 3 éle maradna körút céljára, ezek pedig elvágnák az általuk határolt oktaéderlapot a többiektől.