Kezdőlap


Feladat:	Pontversenyen kívüli P.66	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Füredi Zoltán , Göndőcs Ferenc , Kabay György , Kiss Csaba , Komjáth P. , Pásztor M. , Reviczky J. , Török I. , Varsányi István
Füzet:	1970/december, 217 - 219. oldal		PDF \| MathML
Témakör(ök):	Egyenlőtlenség-rendszerek grafikus megoldása, Elsőfokú (és arra visszavezethető) egyenlőtlenség-rendszerek, Négyzetszámok összege, Kombinatorikus geometria síkban, Kombinatorikai leszámolási problémák, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/április: Pontversenyen kívüli P.66

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük $V_{n}$ -nel az $1,2, ..., n$ egységnyi pálcákból előállítható háromszögek számát, és ezek között legyen $S_{k}$ azoknak a szám $a$ , amelyekben a leghosszabb pálca $k$ egységnyi. Ekkor

\begin{matrix} V_{n} = S_{1} + S_{2} + ... + S_{n} = S_{3} + S_{4} + ... + S_{n}, \end{matrix}

(1)

hiszen

S_{n} = S_{2} = 0

(bár

S_{3}

értéke is

0

, de a későbbiek szempontjából ezt a tagot mégis kiírjuk).
Jelöljük egy tetszőleges háromszögben, amelyben a leghosszabb oldal

k

egységnyi, a másik két oldal hosszát

a

-val,

b

-vel úgy, hogy

\begin{matrix} k > a > b \geq 1. \end{matrix}

(2)

Tehát

a

b

természetes számok, melyekre a háromszög-egyenlőtlenségnek megfelelően

\begin{matrix} a + b > k . \end{matrix}

(3)

Ha az

a

b

természetes számokra (2) és (3) teljesül, akkor van olyan háromszög, melynek oldalai

a

b

és

k

egységnyiek, hiszen a másik két oldalra vonatkozó háromszög-egyenlőtlenség (2) miatt triviálisan teljesül. Ezek szerint

S_{k}

egyenlő a (2) ‐ (3) egyenlőtlenségrendszerre a természetes számok körében adható megoldások számával.
Ha az

a

b

számpárokat a derékszögű koordináta-rendszerben ábrázoljuk, a megfelelő pontok az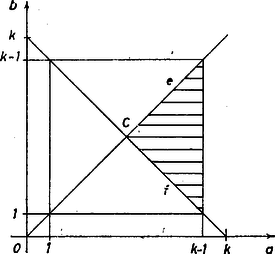

\begin{matrix} 1 \leq a < k, 1 \leq b < k \end{matrix}

egyenlőtlenségekkel meghatározott

N_{k}

négyzetben vannak, az

a = b

feltételnek megfelelő

e

egyenes alatt és az

a + b = k

feltételnek megfelelő

f

egyenestől jobbra.

S_{k}

a síknak ebben a részében található, egész koordinátájú pontjainak (rácspontjainak) száma.

N_{k}

négyzet oldalain

(k - 1)

egész koordinátájú pont van, így

N_{k}

-ban

{(k - 1)}^{2}

a rácspontok száma. Ebből le kell vonnunk az

e

és

f

egyeneseken levő rácspontok számát, ezeken külön-külön ugyancsak

(k - 1)

rácspont található. Ha azonban az

e

és

f

egyenesek metszéspontjának koordinátái egészek, ezt a pontot kétszer számítanánk. A

C

metszéspont mindkét koordinátája,

k / 2

, ezek tehát akkor egészek, ha

k

páros. Ezek szerint ha

N_{k}

-ból elhagyjuk az

e

f

egyenesek pontjait, a visszamaradó rácspontok száma

\begin{matrix} {(k - 1)}^{2} - 2 (k - 1) + λ_{k} = {(k - 2)}^{2} - μ_{k}, \end{matrix}

ahol

λ_{k} = 1

, ha

k

páros, és

λ_{k} = 0

, ha

k

páratlan, és

μ_{k} = 1 - λ_{k}

. Az

N_{k}

négyzetet az

e

f

egyenesek négy egybevágó részre vágják, melyekben a rácspontok száma is egyenlő, hiszen tetszőleges rácspontot ezekre az egyenesekre tükrözve ismét rácspontot kapunk. Ezek alapján

\begin{matrix} S_{k} = \frac{1}{4} ({(k - 2)}^{2} - μ_{k}) . \end{matrix}

(4)

Ha mármost

n

páratlan, akkor (1)-re tekintettel

\begin{matrix} 4 V_{n} = \sum_{k = 3}^{n} {(k - 2)}^{2} - \sum_{k = 3}^{n} μ_{k}, \end{matrix}

ahol a második összeg a

3

és

n

közti páratlan számok száma, hiszen

μ_{k} = 1

k

páratlan, és

μ_{k} = 0

k

páros. Így ez a második összeg

(n - 1)

felével egyenlő és

\begin{matrix} 4 V_{n} & = \sum_{k = 1}^{n - 2} k^{2} - \frac{n - 1}{2} = \frac{(n - 2) (n - 1) (2 n - 3)}{6} - \frac{n - 1}{2} = \\ = \frac{n - 1}{6} (2 n^{2} - 7 n + 3) = \frac{(n - 1) (n - 3) (2 n - 1)}{6} . \end{matrix}

Vagyis páratlan

n

esetén

\begin{matrix} V_{n} = \frac{(n - 1) (n - 3) (2 n - 1)}{24} . \end{matrix}

Ha pedig

n

páros, akkor ezt és (4)-et felhasználva kapjuk, hogy

\begin{matrix} V_{n} & = V_{n + 1} - S_{n + 1} = \frac{n (n - 2) (2 n + 1)}{24} - \frac{{(n - 1)}^{2} - 1}{4} = \\ = \frac{n (n - 2) (2 n + 1)}{24} - \frac{n (n - 2)}{4} = \frac{n (n - 2) (2 n - 5)}{24} . \end{matrix}

A két kifejezést egyesíthetjük. Ugyanis a két számláló beszorzással

\begin{matrix} 2 n^{3} - 9 n^{2} + 10 n - 3, ill. 2 n^{3} - 9 n^{2} + 10 n, \end{matrix}

így minden

n

-re

(n \geq 3)

az egész rész jelének felhasználásával

\begin{matrix} V_{n} = [\frac{n (n - 2) (2 n - 5)}{24}] . \end{matrix}

Göndőcs Ferenc, Füredi Zoltán