Feladat: Pontversenyen kívüli P.63 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bacsó G. ,  Balog J. ,  Bárdossy A. ,  Bihari T. ,  Donga Gy. ,  Fábián K. ,  Ferró J. ,  Frankl P. ,  Földvári Cs. ,  Gulyás A. ,  Göndőcs Ferenc ,  Kirchner I. ,  Kisvarga J. ,  Komócsi S. ,  Komornik V. ,  Less G. ,  Martoni V. ,  Óvári M. ,  Papp G. ,  Petz D. ,  Pressing L. ,  Reviczky J. ,  Selényi Péter ,  Vajnági A. ,  Vargay Gy. ,  Waszlavik L. ,  Zágoni M. 
Füzet: 1970/november, 150 - 155. oldal  PDF  |  MathML 
Témakör(ök): Számkörök, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1970/március: Pontversenyen kívüli P.63

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A feladatban szereplő műveletet egyszerűség kedvéért szorzásnak nevezzük ‐ természetesen erről a szorzásról nem használhatjuk fel a valós számok körében megszokott tulajdonságokat, csak azokat, amelyeket a feladat biztosít. Látni fogjuk, hogy ez a szorzás például nem kommutatív, lesz ugyanis olyan X, Y elempár, melyre X◯Y nem egyenlő Y◯X-szel. Emiatt az elsőre azt mondjuk, hogy X-et jobbról szorozzuk Y-nal, a másodikra, hogy balról.

 

EABCDFGHEEABCDFGHAAEGDBBACCDDHGFFFGGGHEHHEBEABCDFGHEEABCDFGHAABCEFGHDBBCEAGHDFCCEABHDFGDDHGFBAECFFDHGCBAEGGFDHECBAHHGFDAECB
1.ábra5.ábra

A táblázatból leolvasható, hogy bármely elemet az E elemmel akár jobbról, akár balról megszorozva magát az illető elemet kapjuk, az E tehát úgy viselkedik, mint a számok körében az 1-es; emiatt egység-elemnek nevezzük.
A (III) tulajdonság szerint bármely X elemhez van olyan Y elem, mellyel akár jobbról, akár balról megszorozva az egységet kapjuk, ‐ ezt az Y elemet a továbbiakban az X inverzének nevezzük és X'-vel jelöljük. Megmutatjuk, hogy minden elemnek csak egy inverze van. Legyen ugyanis X egy tetszőleges elem, és Y1 is, Y2 is ennek inverze, vagyis
X◯Y1=Y1◯X=X◯Y2=Y2◯X=E,  ekkorY1=Y1◯E=Y1◯(X◯Y2)=(Y1◯X)◯Y2=E◯Y2=Y2,


tehát Y1 és Y2 egyenlőek, állításunkat bebizonyítottuk. (Bizonyítás közben felhasználtuk a II tulajdonságot.) Ha az X elem inverze Y, akkor X◯Y=Y◯X=E, tehát egyben azt is mondhatjuk, hogy Y inverze X, vagyis bármely elem inverzének inverze maga az eredeti elem.
A táblázatból leolvasható, hogy A inverze C, G inverze D, és H inverze F. Az E inverze nyilván E, így B inverze csak B lehet. Rendezzük úgy át a táblázatot, hogy az inverz elemek egymás mellé kerüljenek, és szorzatuk az ábra főátlójában (a jobbra lejtő átlóban) legyen (2. ábra).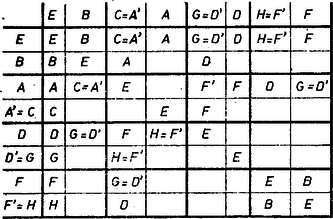
 
 
2. ábra
 

A B-t az E alá (mögé) tettük, így az elemeket kettesével csoportosítva a táblázatban négy vízszintes és négy függőleges sáv alakult ki.
A megadott szorzatokból újakat kapunk, ha felhasználjuk, hogy az (X◯Y) szorzat inverze Y'◯X', hiszen
(X◯Y)◯(Y'◯X')=X◯(Y◯(Y'◯X'))==X◯((Y◯Y')◯X')=X◯(E◯X')=X◯X'=E


Táblázatunkban az X◯Y elem az X jelű sor és az Y jelű oszlop találkozásánál van, az Y'◯X' elem pedig ennek a helynek a főátlóra vett tükörképén, hiszen az Y' elem ugyanannyiadik sorban van, mint ahányadik oszlopban Y áll, és X' ugyanannyiadik oszlopban található, mint ahányadik sorban X áll (4. ábra).
 
 
4. ábra
 

Így a táblázatban megadott szorzatokat a főátlóra tükrözve, és a kapott helyre inverzüket írva, a táblázatnak több mezejét kitölthetjük. (Közben találjuk, hogy F◯C=G, A◯H=D, amint azt vártuk, tehát e két szorzatból az egyiket ,,feleslegesen'' adta meg a feladat.)
A táblázat mostani állásából kiolvasható, hogy F◯F=B. Hasonló állítás igaz az A, D elemekre is: B◯A'=A és B◯D'=D, emiatt
A◯A=(B◯A')◯A=B◯(A'◯A)=B◯E=B,D◯D=(B◯D')◯D=B◯(D'◯D)=B◯E=B.
A szorzat inverzére tett megállapításunkból ennek alapján következik, hogy
A'◯A'=(A◯A)'=B'=B,D'◯D'=(D◯D)'=B'=B,F'◯F'=(F◯F)'=B'=B.

Ezek alapján könnyen kitölthetjük B sorát és oszlopát, hiszen ha X egy tetszőleges, B-től és E-től különböző elemet jelöl, akkor X◯X=B. Ennek alapján (3. ábra)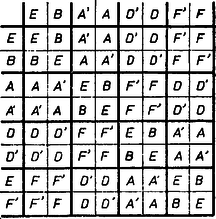
 
 
3. ábra
 

X◯(X◯B)=(X◯X)◯B=B◯B=E,
tehát X◯B az X inverze, és hasonló módon
(B◯X)◯X=B◯(X◯X)=B◯B=E,
tehát B◯X is X inverzével egyenlő.
Mivel B◯B=E, a B elem részben úgy viselkedik, mint a (-1) a valós számok körében, így B◯X=X' miatt X'-t ,,-X''-nek is gondolhatjuk, és azt sejtjük, hogy az előjeles számok szorzásának ismert szabálya itt is érvényes. Valóban, ha X és Y két, az E-től és B-től különböző, de egymástól nem feltétlenül különböző elem, akkor
X'◯Y=(B◯X)◯Y=B◯(X◯Y)=(X◯Y)',X◯Y'=X◯(Y◯B)=(X◯Y)◯B=(X◯Y)',X'◯Y'=(X'◯Y)'=((X◯Y)')'=X◯Y,


ami annak felel meg, hogy különböző előjelűek szorzata negatív, ugyanolyan előjelűek szorzata pozitív a valós számok körében.
Elegendő tehát az A, D, F elemek közti szorzatokat meghatározni. A táblázatból leolvasható, hogy A◯D=F, A◯F=D', D◯A=F' (tehát ez a szorzás valóban nem kommutatív, hiszen A◯D és D◯A nem egyenlőek); a hiányzó szorzatok értéke pedig a már ismert szorzatok alapján:
F◯A=(A◯D)◯A=A◯(D◯A)=A◯F'=(A◯F)'=D,D◯F=(A◯F')◯F=A◯(F'◯F)=A◯E=A,F◯D=(A◯D)◯D=A◯(D◯D)=A◯B=A'.



Ezek alapján már minden hátra levő szorzat értékét meghatározhatjuk és a műveletről összefoglalva kimondhatjuk, hogy
‐ van egy egységelem, az E,
‐ van egy ,,előjel-elem'', a B,
‐ a további elemek inverz párokba állíthatók: A'=C, D'=G, F'=H.
Az inverz elemeket is tartalmazó szorzatokra érvényes az ismert ,,előjelszabály'',
EBC=A'AG=D'DH=F'FEEBC=A'AG=D'DH=F'FBBEADAAC=A'EF'FDG=D'A'=CCEFDDG=D'FH=F'ED'=GGH=F'EFFG=D'EBF'=HHDBE
2. ábra

EBA'AD'DF'FEEBA'AD'DF'FBBEAA'DD'FF'AAA'EBF'FDD'A'A'ABEFF'D'DDDD'FF'EBA'AD'D'DF'FBEAA'EFF'D'DAA'EBF'F'FDD'A'ABE
 

3. ábra
 

‐ az A, D, F elemek közül két egymás utáninak a szorzata ciklikusan mindig a harmadik: A◯D=F, D◯F=A, F◯A=D, a fordított sorrendben pedig a harmadik elem inverzét kapjuk: D◯A=F', F◯D=A', A◯F=D'.
Ennek a műveletnek nyilván megvan az (I), (III) tulajdonsága, azt viszont még meg kell mutatnunk, hogy (II) is mindig teljesül, azaz
(X◯Y)◯Z=X◯(Y◯Z).
Ez nyilván teljesül, ha az elemek közül az egyik E, hiszen ekkor mindkét oldalon a másik két elem szorzata áll. Ha mindhárom elem B, mindkét oldalon B áll, ha csak kettő egyenlő B-vel, akkor mindkét oldalon a harmadik elem áll, ha pedig egy egyenlő B-vel, akkor mindkét oldalon a másik két elem szorzatának az inverze áll. Azt kell még megvizsgálnunk, amikor az X, Y, Z elemek különböznek E-től és B-től.
Ha az X, Y, Z elemeket csak az A, D, F elemek közül választjuk, elegendő azt az esetet vizsgálnunk, amikor X=A, hiszen az A→D, D→F, F→ →A megfeleltetés művelettartó ezekre az elemekre. Így 9 hármasszorzatot kell kétféleképpen kiszámítanunk:
A◯(A◯A)=A◯B=A',(A◯A)◯A=B◯A=A',A◯(A◯D)=A◯F=D',(A◯A)◯D=B◯D=D',A◯(A◯F)=A◯D'=F',(A◯A)◯F=B◯F=F',A◯(D◯A)=A◯F'=D,(A◯D)◯A=F◯A=D,A◯(D◯D)=A◯B=A',(A◯D)◯D=F◯D=A',A◯(D◯F)=A◯A=B,(A◯D)◯F=F◯F=B,A◯(F◯A)=A◯D=F',(A◯F)◯A=D'◯A=F,A◯(F◯D)=A◯A'=E,(A◯F)◯D=D'◯D=E,A◯(F◯F)=A◯B=A',(A◯F)◯F=D'◯F=A'.

Ha az X, Y, Z elemek között az A, D, F elemek inverze is előfordul, az ,,előjelszabály'' alapján mindkét oldalon meghatározhatjuk az eredményt úgy, hogy először elhagyjuk az inverzet jelölő vesszőket, meghatározzuk a szorzatot, majd aszerint, hogy páros vagy páratlan számú vesszőt hagytunk el, a kapott eredményt változatlanul hagyjuk, vagy vesszük az inverzét. ‐ Ezzel a feladat megoldását befejeztük.
 

II. megoldás (csak a táblázat kitöltésére). Bebizonyítjuk a következő segédtételt: az (I)‐(III) tulajdonságokból következik, hogy elemeink mindegyike a táblázat minden egyes sorában, oszlopában föllép. Ebből tovább az következik, hogy minden sorban, oszlopban egyszer lép föl, hiszen a sorok, oszlopok száma egyezik az elemek számával. (Az eredetileg beírt adatok nem mondanak ellent állításunknak.)
U-val és V-vel egy-egy tetszés szerinti elemet jelölve (lehetnek egyezők is), ezt fogjuk bizonyítani: létezik olyan X és olyan Y elem, amelyre
X◯U=V,ill.U◯Y=V,(1)
vagyis, hogy a V elem az U oszlopban is és az U sorban is előfordul. Használjuk az I. megoldásban bevezetett beszédmódot és az inverz elem fogalmát is.
Megkeressük U-nak U' inverzét, továbbá a V◯U' és az U'◯V szorzatot, amelyek (I) szerint léteznek. Ekkor a következő két szorzás ‐ (II)-t is fölhasználva ‐ megadja állításunk bizonyítását:
(V◯U')◯U=V◯(U'◯U)=V◯E=V,U◯(U'◯V)=(U◯U')◯V=E◯V=V.
Ezzel megadtuk az (1)-nek eleget tevő elemet:
X=V◯U',ill.Y=U'◯V,
más szóval: megoldottuk az (1) egyenleteket. Fölhasználtuk azt is, hogy a táblázat teljesen kitöltött 1. sora és 1. oszlopa elemről elemre egyezik a fejrovattal (az oszlopok, sorok jelző betűjével), más szóval azt, hogy E-vel bármelyik elemet akár balról, akár jobbról szorozva, magát az elemet kapjuk.
Segédtételünk alapján beírhatjuk C oszlopának két üres helyére a benne még nem szereplő B és D elemeket, közülük ugyanis az utolsó sorbeli mezőre csak D írható, hiszen az utolsó sorban már van B bejegyzés, ennélfogva B-t a C◯C szorzat eredményének írjuk be (5. ábra, az 1. ábra mellett).
Annak a két ténynek az alapján, hogy C oszlopa immár teljes, és hogy C-nek önmagával való szorzata ‐ röviden: ,,négyzete'' ‐ egyenlő B-vel, jelképesen C2=B, kitölthetjük B teljes oszlopát, C-vel való kétszeri szorzás útján, az
X◯B=X◯(C◯C)=(X◯C)◯C
azonosság fölhasználásával, hiszen az utolsó alak céljára minden X-hez kiolvashatjuk (X◯C)=Y, majd minden adódó Y-hoz (Y◯C) ,,értékét''. Példaképpen előbb a B oszlop már meglevő két bejegyzését ellenőrizzük:
E◯B(  azaz  X=E)  céljára:E◯C=CésC◯C=B,D◯B(  azaz  X=D)  céljára:D◯C=FésF◯C=G,


ez a két adat tehát megegyezésben van ‐ nincs ellentmondásban ‐ az eddig fölhasználtakkal. Hasonlóan X=A mellett A◯C=E és E◯C=C, tehát A◯B=C; az oszlop további hiányzó elemei pedig rendre E, A, H, D, F, egymástól és az előbbiektől különbözők, az oszlop önmagában ellentmondástalan. (A segédtétel szerinti, valamint az eddigi bejegyzésekhez viszonyított ellentmondástalanságot a továbbiakban nem mondjuk ki, bár természetesen ellenőrizzük, hiszen ellentmondás föllépése hiábavalónak mutatná a további munkát.)
Most már a B oszlop teljes voltát is fölhasználva, hasonlóan kitölthetjük B◯C=A oszlopát, a vele jobbról való szorzást is két szorzásra felbontva:
X◯A=X◯(B◯C)=(X◯B)◯C,
a hiányzó betűk rendre B, C, E; D, F, G.
Eddigi fogásunk nem használható további teljes oszlopok kitöltéséhez, mert az eddig kitöltött oszlopokhoz tartozó A, B, C elemek, valamint az eleve teljes oszlopú E közül bármelyik kettőnek bármelyik sorrendben vett szorzata sem ad ,,új'' elemet, szemléletesen mondva: a táblázat bal felső negyedében nem fordul elő D, F, G, H egyike sem.
Kitölthetjük viszont az A sor még üres két mezejét, a sor még nem használt szorzatai és az eddigiek alapján:
A◯D=A◯(H◯C)=(A◯H)◯C=D◯C=F,A◯G=A◯(F◯C)=(A◯F)◯C=G◯C=H.



Ezekre támaszkodva B, majd C sora válik teljessé
B◯X=(A◯A)◯X=A◯(A◯X)  ésC◯X=(A◯B)◯X=A◯(B◯X)
alapján ‐ most jobbról bal felé haladva a kiszámításban ‐ a sor végén G, H, D, F, ill. H, D, F, G bejegyzésekkel. Hasonlóan H sorában
H◯D=H◯(H◯C)=(H◯H)◯C=B◯C=A  ésH◯G=H◯(F◯C)=(H◯F)◯C=E◯C=C,
végül e sor és a következő azonosságok alapján rendre G, F, D sorát tesszük teljessé:
G◯X=(H◯A)◯X=H◯(A◯X),F◯X=(G◯A)◯X=G◯(A◯X)  ésD◯X=(F◯A)◯X=F◯(A◯X)
(könnyítésül megjegyezzük, hogy a jobb oldal szerinti, időben első szorzás mindháromban ugyanaz).
 

Selényi Péter és Göndőcs Ferenc

megoldásainak felhasználásával