|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Bebizonyítjuk a következő segédtételt: két adott, közös pont nélküli, zárt, konvex alakzat elválasztható egy síkkal; pontosabban: megadható hozzájuk olyan sík, hogy az általa meghatározott, nyílt félterek mindegyike az egyik ‐ és csak az egyik ‐ alakzatot tartalmazza.
Könnyen bizonyítható, hogy ha és két zárt, konvex alakzat, akkor létezik olyan -beli és hozzá egy -beli pont, hogy -vel a -nek, -vel a -nek egy-egy tetszőleges pontját jelölve, a távolság legalább akkora, mint a távolság. Ha -nek és -nek nincs közös pontja ‐ mint esetünkben ‐, akkor , és különbözők. Ekkor a szakasz felező merőleges síkja egy, a fentiek szerinti elválasztó sík, és elválasztja -et -től minden olyan sík is, amely ezzel párhuzamos és a szakaszt ennek egy belső pontjában metszi.
Az állítást az ilyen -ekre bizonyítjuk. Előrebocsátjuk, hogy a mondottak szerint a körüli, sugarú gömbnek nyilvánvalóan nincs közös belső pontja -vel.
Tegyük föl ‐ állításunkkal ellentétben ‐, hogy -nek van az -sel közös pontja. Ez nem azonos -vel, mert nincs rajta -en. Így a szakasz minden pontja beletartozik -be, mert konvex. Van tehát e szakasznak ‐ és vele -nek is ‐ a belsejébe eső pontja, bárhol van is az -en, ugyanis -től felé indulva közeledünk -hez, belépünk -be, hiszen -nek -beli érintősíkja párhuzamos -sel. Így pedig , ami ellentmondás; -nek nincs tehát pontja -en.
Nem lehet pontja -nek a -et tartalmazó féltérben sem, mert ha volna, akkor az ezt -vel összekötő szakasz átdöfné -et, és a szakasszal együtt a döféspont is -be tartoznék, aminek lehetetlen voltát már beláttuk. ‐ Az indexek fölcserélésével -re is érvényes állításunk.
2. A feladat feltevése nem zárja ki, hogy a három test közül csak kettőt választva, ezeknek legyen közös pontja.
3. Segédtételünk alapján könnyű belátni a feladat állítását arra az esetre, ha van a három konvex test között olyan kettő, melyeknek nincs közös pontja. Ugyanis ezt a két testet véve az előbbi és szerepére, továbbá vetítési iránynak egy -beli egyenes irányát, végül egy az irányhoz hajló (azaz hegyes vagy derékszöget bezáró) síkot, e síkon mindhárom test vetülete létrejön, és az első két vetületnek nem lesz közös pontja. Valóban, így vetülete egyenes, a félterek vetületei nem nyúlnak egymásba, ugyanígy és -éi sem, ekkor pedig a három vetületnek sem lehet közös pontja.
4. Ha pedig nincs a három test: , és közt a fenti és szerepére alkalmas pár ‐ vagyis bármelyik kettőnek van közös pontja, akkor a 3. pont meggondolását először a és testek közös részére alkalmazzuk. Ez feltevésünk szerint nem üres, továbbá nyilvánvalóan zárt és konvex, végül a feladat föltevése szerint nincs közös pontja -mal, van tehát olyan sík a segédtétel szerint, amely elválasztja -t -tól.
Ekkor a -at tartalmazó zárt féltérben -nek is, -nek is van része, e , részeknek azonban nincs közös része, továbbá nyilvánvalóan mindkét rész zárt és konvex. Így megadható egy őket szétválasztó sík (minket azonban ennek csak az a félsíkja érdekel, amely a -at tartalmazó féltérben van). Ekkor -nek -gyel való metszésvonala alkalmas vetítési irány. Valóban, így vetülete egy egyenes, mondott félsíkjának vetülete egy félegyenes és ezek úgy vágják szét a vetítési síkot, hogy vetülete -nek egyik oldalán van, és elválasztja és vetületét.
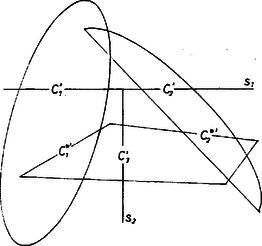
A mondott vetítési irány egyértelműen létezik, mert sem azonos, sem párhuzamos nem lehet -gyel, hiszen -en van -beli pont is, -beli is, és ezek szétválasztására sem maga nem alkalmas, sem egy vele párhuzamos sík. Ezzel a bizonyítást befejeztük. |
 PDF |
PDF |  MathML
MathML 