Kezdőlap


Feladat:	Pontversenyen kívüli P.60	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balog János , Donga György , Ferró József , Földvári Csongor , Göndőcs Ferenc , Lempert László , Szabó György , Várady Tamás
Füzet:	1972/május, 210 - 214. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek hasonlósága, Négyszögek geometriája, Párhuzamos szelők tétele, Térgeometriai bizonyítások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/február: Pontversenyen kívüli P.60

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1 ‐ 3. ábrák különböző fölvételekben mutatják be a feladat föltevéseit és állítását.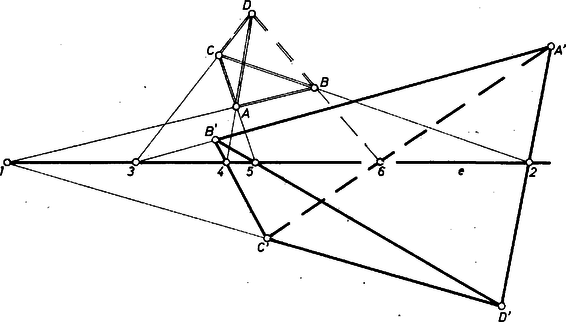

1. ábra

Megjegyezzük, hogy konvexség nincs föltételezve a négyszögekről. így az ,,oldal'' ,,átló'' nevek használatának nincs helye; e természetesen át is haladhat a négyszögeken.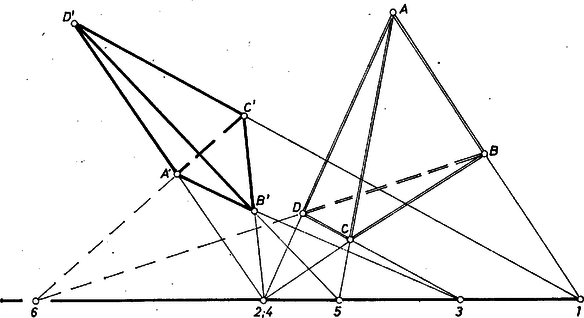

2. ábra

A speciális fölvételű 2. ábrán az (1)-beli második és negyedik metszéspont egybeesik; a 3. ábrán pedig

B C

és

A' D'

e

-vel párhuzamosak, ekkor is igaznak mutatja az állítást a szemlélet.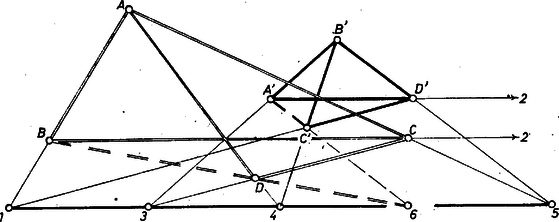

3. ábra

‐ Belátjuk viszont mindjárt most, hogy négyszögeinknek ‐ amennyiben nem elfajult négyszögek ‐ magán az

e

egyenesen nem lehet rajta egy szögpontjuk sem. Ha ugyanis pl.

A

volna rajta az

e

-n - vagyis az (1)-ben háromszor szereplő pontok egyike ‐, akkor itt metszené

e

-t az

A B

A C

A D

egyenes és ezek révén a

C' D'

és

B' D'

, végül a

B' C'

egyenes is, így

C'

D'

és

B'

vagy egy egyenesen volnának, vagy egybe is esnének

A

-val, vagyis az

A' B' C' D'

négyszög mindenképpen elfajult volna. Ha pedig

B

volna

e

-n ‐ vagyis az (1)-ben csak kétszer szereplő pontok egyike ‐, akkor itt metszené

e

-t

B A

és

C' D'

, valamint

B C

és

D' A'

, tehát hasonlóan

D'

azonos volna

B

-vel, márpedig

D'

az (1)-ben azonos szerepű

A

-val, tehát ez sem lehetséges. (Ha valamelyik négyszögnek két szögpontja volna rajta

e

-n, akkor az (1) metszések közül a megfelelő határozatlan lenne.)
2. A bizonyítás céljára térbeli centrális vetítéssel a két négyszög és az

e

egyenes alakzatáról olyan képet állítunk elő, egy, az eredeti síkot metsző síkon, amelyben az (1) egyenespárok elemei páronként párhuzamosak. Ezután bebizonyítjuk, hogy a kérdéses

B D

A' C'

egyenesek képei is párhuzamosak. Ebből az eredményből az állítás igaz voltát a vetítés tulajdonságai alapján fogjuk kikövetkeztetni.
Legyen

O

egy, az alakzatunk

S

síkján kívül álló pont és

S_{1}

egy, az

O

és

e

által meghatározott

S'_{1}

síkkal párhuzamos, de attól különböző, rögzített sík. Egy

S

-beli

P

pont

P_{1}

képét az

O P

egyenes (a vetítő sugár)

S_{1}

-en lévő döféspontjaként értelmezzük (4. ábra).

4. ábra

P_{1}

akkor és csak akkor nem létezik, ha

P

rajta van

e

-n (ekkor

O P

párhuzamos

S_{1}

-gyel); különben

P_{1}

egyértelműen létrejön. ‐ Fordítva,

P_{1}

képe

P

, és

S_{1}

minden

Q_{1}

pontjának

S

-beli képe egyértelműen az

Q Q_{1}

egyenes által kimetszett

Q

pont, kivéve annak az

e^{*}

egyenesnek a pontjait, amelyet az

O

-n át

S

-sel párhuzamosan fektetett

S'

sík metsz ki

S_{1}

-ből, ezeknek a pontoknak nincs képe ebben a leképezésben (ekkor

Q Q_{1}

párhuzamos

S

-sel).
Továbbmenve, ha az

S

-nek

f

és

g

egyenesei az

e

-n levő

E

pontban metszik egymást, akkor

f_{1}

g_{1}

képeik párhuzamosak, hiszen nyilvánvalóan át kellene menniük

E

képén,

E

-nek viszont nincs képe. (Másképpen:

f

és

g

vetítősíkjai az

O E

egyenesben metszik egymást, ez párhuzamos

S_{1}

-gyel, tehát a vetítősíkoknak

S_{1}

-gyel alkotott metszésvonalai, a képek is párhuzamosak. Egyébként

f

és

f_{1}

S

-nek és

S_{1}

-nek

t

metszésvonalán metszik egymást.) Hasonlóan látható be, hogy akkor is párhuzamosak

f

és

g

képei, ha mindkettő párhuzamos

e

-vel, és különböző tőle; ekkor

f_{1}

és

g_{1}

párhuzamosak

t

-vel

(t ∥ e)

.
Fordítva: ha

f_{1}

és

g_{1}

S_{1}

-ben egymással párhuzamos, de

S

-sel nem párhuzamos egyenesek, akkor ezek képei

e

-n metszik egymást, mert az

O

f_{1}

és

O

g_{1}

vetítősíkok metszésvonala párhuzamos

S_{1}

-gyel, benne van

S'_{1}

-ben, tehát metszi

e

-t, és a metszésponton átmegy az

f

, ill. a

g

kép. Ha pedig

f_{1}

és

g_{1}

S_{1}

-nek

S

-sel, azaz

t

-vel párhuzamos egyenesei, akkor ezek

S

-beli

f

és

g

képe párhuzamos egymással és

e

-vel.
3. A legutóbbiak, valamint a feladat föltevései és az 1. pontbeli megjegyzés szerint az

A B C D

és

A' B' C' D'

négyszögek csúcsainak

A_{1}, B 1, ... D'_{1}

képei a végesben vannak és

\begin{matrix} A_{1} B_{1} ∥ C'_{1} D'_{1}; B_{1} C_{1} ∥ D'_{1} A'_{1}; C_{1} D_{1} ∥ A'_{1} B'_{1}; D_{1} A_{1} ∥ B'_{1} C'_{1}; A_{1} C_{1} ∥ B'_{1} D'_{1} \end{matrix}

(2)

(5. ábra).

5. ábra

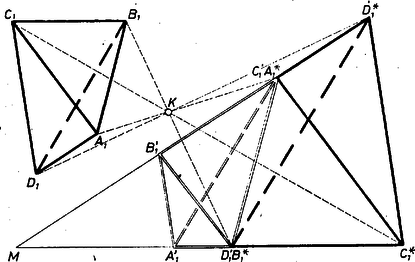Tekintsük az első kapcsolat alapján azt a hasonlósági transzformációt, mely

A_{1}

-et

C'_{1}

-be és

B_{1}

-et

D'_{1}

-be viszi át; ennek középpontja az

A_{1} C'_{1}

és

B_{1} D'_{1}

egyenesek

K

metszéspontja ‐ amennyiben létezik. (Ez a nyújtás vagy zsugorítás természetesen a

K

-ra való tükrözést is tartalmazhatja, ilyenkor a nagyítási arányszám negatív.) Legyen

C_{1}

D_{1}

képe ebben a hasonlóságban

C_{1}^{*}

D_{1}^{*}

(továbbá

C'_{1}

egyben

A_{1}^{*}

és

D'_{1}

egyben

B_{1}^{*}

), (2) szerint

C_{1}^{*}

A'_{1} D'_{1}

egyenesen,

D_{1}^{*}

pedig a

B'_{1} C'_{1}

egyenesen van.
Az

A'_{1} D'_{1}

és

B'_{1} C'_{1}

egyenesek általában metszik egymást egy

M

pontban. Alkalmazzuk ebben az esetben a párhuzamos szelők tételét az

M

csúcsú szög száraira és egyrészt a

B'_{1} D'_{1}

A_{1}^{*} C_{1}^{*}

szelőkre (amelyek párhuzamosak egymással, hiszen mindkettő párhuzamos

A_{1} C_{1}

-gyel), másrészt az

A'_{1} B'_{1}

C_{1}^{*} D_{1}^{*}

szelőkre:

\begin{matrix} \frac{M B_{1}^{*}}{M B'_{1}} = \frac{M C_{1}^{*}}{M C'_{1}}, illetve \frac{M B'_{1}}{M A'_{1}} = \frac{M D_{1}^{*}}{M C_{1}^{*}} . \end{matrix}

Ezeket összeszorozva

\begin{matrix} \frac{M B_{1}^{*}}{M A'_{1}} = \frac{M D_{1}^{*}}{M C'_{1}}, \end{matrix}

ami ugyanazon tétel szerint azt jelenti, hogy a

B_{1}^{*} D_{1}^{*}

egyenes párhuzamos az

A'_{1} C'_{1}

egyenessel. Hasonlósági transzformációnk szerint viszont

B_{1}^{*} D_{1}^{*} ∥ B_{1} D_{1}

tehát

B_{1} D_{1} ∥ A'_{1} C'_{1}

. Ez pedig a 2. pont utolsó megállapításai szerint a feladat állítását bizonyítja, ha

B_{1} D_{1}

nem párhuzamos

t

-vel, akkor

B D

és

A' C'

e

-n metszik egymást, ha pedig

B D ∥ t

, akkor

B D ∥ A' C' ∥ e

. (A bizonyításban (2)-nek mindegyik kapcsolatát felhasználtuk.)
Az iménti

M

pont csak akkor nem jön létre, ha

A'_{1} D'_{1} ∥ B'_{1} C'_{1}

(6. ábra), azaz ha (2) szerint

B_{1} C_{1}

is,

D_{1} A_{1}

is párhuzamos velük.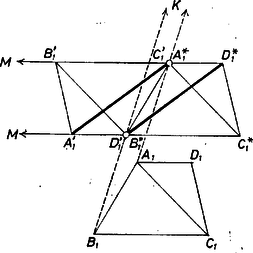

6. ábra

Ekkor, mivel megfelelő oldalaik párhuzamosak, a

D_{1} C_{1} A_{1}

háromszög hasonló az

A'_{1} B'_{1} D'_{1}

háromszöghöz, a

D_{1}^{*} C_{1}^{*} A_{1}^{*}

háromszög pedig egybevágó az utóbbival, hiszen az egymásnak megfelelő

C_{1}^{*}

ill.

B'_{1}

csúcsból induló magasságuk egyenlő. így pedig

D_{1}^{*} A_{1}^{*} \equiv D_{1}^{*} C'_{1} # D'_{1} A'_{1} \equiv B_{1}^{*} A'_{1}

, tehát

D_{1}^{*} C'_{1} A'_{1} B_{1}^{*}

paralelogramma, és

A'_{1} C'_{1} ∥ B_{1}^{*} D_{1}^{*} ∥ B_{1} D_{1}

; ezzel az állítást ilyen esetre is bebizonyítottuk. (Az

A_{1} D_{1} ∥ B_{1} C_{1}

helyzet azt jelenti, hogy

S

-ben

A D

és

B C

ugyanabban a pontban metszik

e

-t, és az egyszersmind a

B' C'

és

A' D'

egyeneseknek is a metszéspontja, 2. ábra.)
A felhasznált

K

hasonlósági középpont pedig csak akkor nem létezik, ha

A_{1} C'_{1} ∥ B_{1} D'_{1}

. Ekkor

A_{1} B_{1} D'_{1} C'_{1}

paralelogramma, és

A_{1} B_{1}

(és vele

A_{1} B_{1} C_{1} D_{1}

) transzlációval (egybevágósági transzformációval) vihető át

C'_{1} D'_{1}

-be (ill.

A'_{1} B'_{1} C'_{1} D'_{1}

mellé; a 6. ábra egyszersmind erre is példát mutat).
4. Mindezek szerint a feladat eredeti alakzatának

O

-n át

S_{1}

-be vetítésével arra az esetre is bebizonyítottuk az állítást, ha az (1) egyenespárok közt van az

e

-vel párhuzamos pár is. (Legföljebb két ilyen pár lehet, mert pl.

A

B

C

és

D

mindegyikén át a szóban forgó

3 - 3

egyenes közül csak egy lehet párhuzamos

e

-vel.)

Megjegyzés. A feladat állítása ekvivalens a következővel: négy pont (a síkon), melyek közül semelyik három sincs egy egyenesen,

6

egyenest határoz meg, ezek közül

5

-nek egy adott (egyik adott ponton sem átmenő) egyenessel való metszéspontjai egyértelműen meghatározzák a hatodik egyenesnek az adott egyenessel való metszéspontját. Erre az állításra közvetlen bizonyítások is adhatók.