Kezdőlap


Feladat:	Pontversenyen kívüli P.58	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balog J. , Ferró J. , Füredi Z. , Földvári Cs. , Göndőcs F. , Kirchner I. , Lempert L. , Less Gy. , Martoni V. , Nagy Ágnes , Papp Z. , Reviczky J. , Szabó György , Vajnági A. , Várady T. , Waszlavik L.
Füzet:	1970/november, 145 - 147. oldal		PDF \| MathML
Témakör(ök):	Klasszikus valószínűség, Geometriai valószínűség, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/február: Pontversenyen kívüli P.58

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Feladatunk első részét általánosabban oldjuk meg: azt tesszük fel, hogy a kör kerületét $6 n$ egyenlő részre osztjuk; ekkor a feladatban mondott eljárást $n = 30$ mellett kapjuk. Mérjük a kerület pontpárjainak távolságát az általuk meghatározott (kisebbik) körív hosszával, és válasszuk egységnek a kerület $6 n$ -ed részét. Egy választott háromszög nyilván akkor szokványos, ha csúcsainak távolsága legalább $n$ .
Mivel minden ponthármast egyenlő valószínűséggel választunk, a kérdezett valószínűség a választható szokványos háromszögek és az összes választható háromszög számának a hányadosával egyenlő. Számláljuk össze a háromszögeket úgy, hogy csúcsaikat egymás után határozzuk meg. Így minden háromszöget (választhatót is, szokványosat is) $6$ -szor számolunk, hiszen $3$ csúcsát $6$ sorrendben határozhatjuk meg, a keresett hányados értéke tehát változatlan marad. Összesen $6 n (6 n - 1) (6 n - 2)$ háromszöget kapunk, hiszen az első csúcs a $6 n$ osztópont bármelyike lehet, és a másodikat, harmadikat a visszamaradó $6 n - 1$ , illetve $6 n - 2$ osztópont közül választhatjuk.
Egy szokványos háromszög első csúcsát ugyancsak $6 n$ -féleképpen választhatjuk meg. Jelöljük a választott osztópontot $A_{0}$ -lal, és ebből kiindulva pozitív forgásirányban a további osztópontokat jelölje rendre $A_{1}$ , $A_{2}$ , $...$ , $A_{6 n - 1}$ . Mivel a második csúcsot az elsőtől legalább $n$ távolságra kell választanunk, azt csak az $A_{n}, A_{n + 1}, ..., A_{5 n}$ , osztópontok közül választhatjuk. Tegyük fel, hogy második csúcsnak $A_{k}$ -t választottuk, ahol tehát $n \leq k \leq 5 n$ , és válasszuk a harmadik csúcsot a pozitív forgásirány szerint $A_{k}$ után, de $A_{0}$ előtt. A harmadik csúcsnak $A_{k}$ -tól is, $A_{0}$ -tól is legalább $n$ távolságra kell lennie, ilyen pont csak akkor van, ha $A_{k}$ -tól pozitív forgás szerint $A_{0}$ legalább $2 n$ távolságra van, vagyis $k \leq 4 n$ . Ha ez teljesül, akkor a harmadik csúcsot az

\begin{matrix} A_{k + n}, A_{k + n + 1}, ..., A_{5 n} \end{matrix}

osztópontok közül választhatjuk, ami e csúcs választására

\begin{matrix} 5 n - (k + n - 1) = 4 n - k + 1 \end{matrix}

lehetőséget jelent.

k

lehetséges értékeit is figyelembe véve, ha a 3. csúcsot a 2. után választjuk, e két csúcs választására

\begin{matrix} \sum_{k = n}^{4 n} (4 n - k + 1) = \sum_{j = 1}^{3 n + 1} j = \frac{(3 n + 1) (3 n + 2)}{2} \end{matrix}

lehetőségünk van, ha azt akarjuk, hogy a kapott háromszög szokványos legyen. Nyilván ugyanennyi a lehetőségek száma, ha a 3. csúcsot a 2. csúcs előtt választjuk, az összes kiválasztás száma tehát (figyelembe véve az első csúcs választását is)

6 n (3 n + 1) (3 n + 2)

.
Ezek szerint szokványos háromszög választásának valószínűsége

\begin{matrix} p_{n} = \frac{6 n (3 n + 1) (3 n + 2)}{6 n (6 n - 1) (6 n - 2)} = \frac{(3 n + 1) (3 n + 2)}{(6 n - 1) (6 n - 2)}, \end{matrix}

Ennek értéke

n = 1

mellett

1

, ami közvetlenül is látható: ha a csúcsokat egy szabályos hatszög csúcsai közül választjuk (1. ábra), akkor minden háromszög szokványos.

1. ábra

n

értékét növelve

p_{n}

értéke monoton csökken, és

n = 30

mellett

\begin{matrix} p_{30} = \frac{91 \cdot 92}{179 \cdot 178} = 0, 263. \end{matrix}

b) Tegyük fel ismét, hogy a csúcsokat egymás után választjuk meg. Az első csúcs választásának még semmi hatása nincs a kialakuló háromszög alakjára, tegyük fel, hogy ezt már megválasztottuk a kör kerületén. Az, hogy a második csúcsot tetszőlegesen választjuk a kerületen, pontosabban azt jelenti, hogy ha kijelölünk egy ívet a kerületen, akkor annak a valószínűsége, hogy a második csúcsot a mondott íven választjuk, arányos az ív hosszával. Válasszuk egységnyinek a kör kerületét, és határozzuk meg a második csúcs helyzetét az első csúcstól pozitív forgásirányban mért távolságával, jelöljük azt az értéket

x

-szel.

x

értékét tehát

0

és

1

között választjuk ,,tetszőlegesen'', amit az előbb megfogalmazott módon mondhatunk pontosabban. Hasonlóan választhatjuk a harmadik csúcsot is, ennek helyét a

0

és

1

közötti

y

számmal fogjuk jellemezni.
Meg kell állapítanunk, mi a kapcsolat a két érték választása között. Azt szeretnénk, ha a két érték választása között ,,semmi kapcsolat'' sem volna, ezt azonban nem tudjuk pontosabban megfogalmazni. Elérjük azonban, amit akarunk, ha az

x

y

értékeket egy

P

pont két koordinátájának tekintjük, és a

P

pontot választjuk a sík egységnégyzetében ,,tetszőlegesen''. Ez utóbbit ismét meg tudjuk pontosan fogalmazni: akkor választjuk

P

-t tetszőlegesen a négyzetben, ha annak valószínűsége, hogy

P

-t a négyzet valamely adott tartományában választjuk, arányos e tartomány területével. (Mivel a négyzet területe egységnyi, e valószínűség egyszerűen egyenlő a tartomány területével.)
Meg kell tehát határoznunk, az egységnégyzet melyik részén vannak azok a pontok, melyeknek szokványos háromszögek felelnek meg. Tegyük fel először, hogy

x < y

, ekkor a csúcsok közti ívek hossza, rendre

x

y - x

1 - y

. A háromszög akkor szokványos, ha ezek nem kisebbek a teljes kerület hatodánál, azaz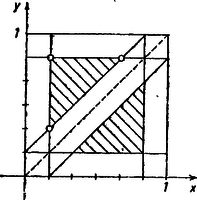

\begin{matrix} x \geq \frac{1}{6}, y - x \geq \frac{1}{6}, 1 - y \geq \frac{1}{6} . \end{matrix}

Ezek az egyenlőtlenségek egy derékszögű háromszöget határoznak meg, csúcsainak koordinátái:

(\frac{1}{6}; \frac{1}{3})

(\frac{1}{6}; \frac{5}{6})

(\frac{2}{3}; \frac{5}{6})

, és befogóinak hossza

\frac{1}{2}

(2. ábra).

2. ábra

x > y

esetnek megfelelő tartományt az

x

y

szerepének felcserélésével kapjuk, ez tehát az előbbi háromszögnek az

y = x

egyenesre vonatkozó tükörképe. E két háromszög területének összege

1 / 4

, ez egyben a szokványos háromszög választásának a valószínűsége is.

Megjegyzés. A kapott eredmény megegyezik az a) részben kapott

p_{n}

határértékével, ha

n

tart a végtelenbe. Ez azt mutatja, hogy helyesen adtuk meg a b) részben a ,,tetszőleges'' választás pontos megfogalmazását. Pusztán e határérték meghatározását azonban nem tekinthetjük a b) rész megoldásának, hiszen ennél ‐ mint láttuk ‐ a lényeges nehézséget épp a feladat pontos megfogalmazása okozta. Ez igen gyakran előfordul a valószínűségszámítással kapcsolatos feladatoknál ‐ és arra is könnyű példát mutatni, hogy ha a szemléletesen megfogalmazott feladatot pontosabbá akarjuk tenni, akkor erre többféle eljárás is megadható, és ezeknél a végeredmény is eltérő lehet. Feladatunkban ezt az a hallgatólagos feltevés zárta ki, hogy a b) részben az a) részhez hasonló eljárást kívántunk meghatározni.