Kezdőlap


Feladat:	Pontversenyen kívüli P.57	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balog János , Füredi Zoltán , Göndőcs Ferenc , Horváth Miklós , Kirchner Imre , Lempert László , Papp Zoltán , Pintér István , Reviczky János , Vajnági András , Várady Tamás , Waszlavik László
Füzet:	1970/október, 72 - 75. oldal		PDF \| MathML
Témakör(ök):	Elsőfokú (és arra visszavezethető) egyenletrendszerek, Magasabb rendű számtani sorozat, Számsorozatok, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1970/február: Pontversenyen kívüli P.57

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott oszlopokban álló $3 - 3$ szám összege valóban 8, négyzetük összege pedig köbszám:

\begin{matrix} ..., 30^{3}, 10^{3}, 6^{3}, 18^{3}, 46^{3}, ... \end{matrix}

Feladatunk szerint az egyes sorok egy-egy mindkét irányban végtelen sorozat elemei, jelöljük ezeket rendre

a_{k}

b_{k}

c_{k}

-val, négyzetük összegének köbgyökét pedig

d_{k}

-val

(k = 0, \pm 1, \pm 2, ...)

. Válasszuk úgy a jelölést, hogy a

k = 0

indexnek a középső oszlop feleljen meg. Úgy akarjuk ezeket a sorozatokat meghatározni, hogy

\begin{matrix} a_{k} + b_{k} + c_{k} & = 8, & (1) \\ a_{k}^{2} + b_{k}^{2} + c_{k}^{2} & = d_{k}^{3} & (2) \end{matrix}

teljesüljön minden egész

k

-ra. Láttuk, hogy (1) és (2) teljesül

k = 0

\pm 1

\pm 2

mellett.
Tájékozódásul ábrázoljuk az adott számokat mint

k

függvényét.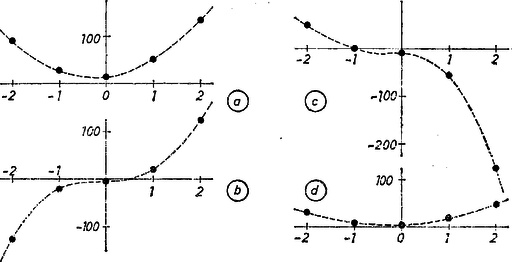

a_{k}

és

d_{k}

sorozatból kapott pontok egy-egy parabolán látszanak elhelyezkedni. Határozzuk meg ezeket a parabolákat rendre a középső három pont alapján:

\begin{matrix} a_{k} & = A k^{2} + B k + C, \\ a_{- 1} & = A - B + C = 26, \\ a_{0} & = C = 14, \\ a_{1} & = A + B + C = 50. \end{matrix}

Ezek alapján

C = 14

A - B = 12

A + B = 36

A = 24

B = 12

\begin{matrix} a_{k} = 24 k^{2} + 12 k + 14. \end{matrix}

(3)

Hasonlóan kapjuk, hogy

\begin{matrix} d_{k} = 8 k^{2} + 4 k + 6, \end{matrix}

(4)

és a behelyettesítés mutatja, hogy (3) és (4) érvényes

k = \pm 2

mellett is.
A

b_{k}

és

c_{k}

sorozatok adott értékei inkább harmadfokú függvényre emlékeztetnek, ezeket a

k = \pm 1, \pm 2

értékek alapján határozzuk meg:

\begin{matrix} b_{k} & = A k^{3} + B k^{2} + C k + D, \\ b_{- 2} & = - 8 A + 4 B - 2 C + D = - 130, \\ b_{+ 2} & = 8 A + 4 B + 2 C + D = 126, \\ b_{- 1} & = - A + B - C + D = - 18, \\ b_{+ 1} & = A + B + C + D = 14; \\ \frac{1}{2} (b_{- 2} + b_{2}) = 4 B + D = - 2, \\ \frac{1}{2} (b_{- 1} + b_{1}) = B + D = - 2, \\ B = 0; \end{matrix}