Kezdőlap


Feladat:	Pontversenyen kívüli P.52	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Göndőcs Ferenc , Lempert László
Füzet:	1971/március, 121 - 123. oldal		PDF \| MathML
Témakör(ök):	Forgatva nyújtás, Merőleges affinitás, Ellipszis egyenlete, Kúpszeletek érintői, Ellipszis, mint kúpszelet, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/december: Pontversenyen kívüli P.52

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje a két egyenest $e$ és $f$ , metszéspontjukat $A$ , a két adott pontot $G$ és $H$ , a $G H$ egyenes metszéspontját $e$ -vel $E$ , $f$ -fel $F$ (legalább az egyikük létezik). Nyilvánvalóan csak akkor lehet szó megoldásról, ha $G$ és $H$ az egyenesek alkotta négy síknegyed közül ugyanabba esik, ezt tehát föltesszük. Elég megszerkesztenünk a keresett $k$ ellipszisnek $e$ -vel és $f$ -fel való $B$ , ill. $C$ érintkezési pontját, mert ekkor $O$ középpontja az $e$ -re $B$ -ben és $f$ -re $C$ -ben emelt merőlegesek metszéspontja, hiszen az ellipszis tengelyeinek végpontjában az érintő merőleges az illető tengelyre; a $B$ , $C$ , $O$ ponthármassal $k$ -t meghatározottnak vesszük.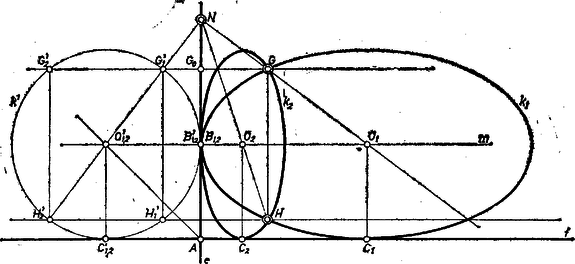
Tekintsük $k$ képét az $e$ tengelyű merőleges affinitásokban, az affinitás $λ$ arányszámát változtatva. Jobb áttekintés érdekében csak az $e$ másik partján keletkező képekre szorítkozunk, azaz ha $λ < 0$ . Így $O$ képe az $e$ -re merőleges egyenesen mozog és ha $- λ = O C / O B$ , akkor $k$ képe egy $k'$ kör lesz, melynek sugara egyenlő $O C$ -vel. (Értelemszerűen ugyanezek mondhatók az $f$ tengelyű merőleges affinitásokban is $k$ képeiről.)
Már ezek alapján könnyen célhoz érünk minden olyan esetben, ha a $G H$ szakasz párhuzamos az adott egyenesek egyikével, mondjuk $e$ -vel. Ilyenkor ugyanis affin képe, $G' H'$ is párhuzamos $e$ -vel, és a kép felező merőlegese ‐ ami azonos magának a $G H$ szakasznak $m$ felező merőlegesével, hiszen $G' H'$ a $G H$ -ból $f$ irányú alkalmas eltolással is előállítható ‐ kimetszi $e$ -ből $B$ -t; továbbmenve $k'$ -nek $O'$ középpontját $m$ -ből kimetszhetjük az $e$ , $f$ egyenespárnak azzal a szögfelezőjével, amely a $G'$ -t tartalmazó síknegyedben halad, és így $k'$ az $O'$ közepű, $O' B$ sugarú kör (1. ábra).

1. ábra

k'

-ból a

G

-nek (és

H

-nak is) két megfelelőjét metszi ki a rajta átmenő,

e

-re merőleges egyenes:

G'_{1}

-et¹

\to

és

G'_{2}

-t (azaz pl.

- λ_{1} = G'_{1} G_{0} / G G_{0}

, ahol

G_{0}

G

vetülete

e

-re), a két megoldásra tekintettel írtuk

O'

helyére az

O'_{1,2}

jelet. Mármost a megfelelő két ellipszis

O_{1}

O_{2}

középpontját

m

-en úgy kapjuk, hogy

G

-t, ill.

H

-t összekötjük a körrendszerbeli

O'_{1} G'_{1}

, ill.

O'_{2} H'_{2}

egyenesnek

e

-n levő (közös)

N

pontjával, végül

O_{1}

O_{2}

vetülete

f

-en

C_{1}

, ill.

C_{2}

.
A továbbiakban föltesszük, hogy

E

és

F

mindegyike létezik, és

G

H

köztük levő (különböző) pontok. Ha feladatunkat úgy módosítanánk, hogy egyrészt az adott

e

és

f

helyett egy-egy az

E

-n, ill.

F

-en átmenő egyenest kelljen szerkeszteni úgy, hogy merőlegesen álljanak egymásra ‐ ami természetesen a követelmény lazítása ‐, másrészt ellipszis helyett kört kelljen szerkeszteni ‐ ami viszont megszigorítása a követelménynek ‐, akkor éppen a P. 39. problémával állnánk szemben.² Megmutatjuk, hogy feladatunk e két módosítást követve visszavezethető a P. 39-beli szerkesztésre.
Legyen

G

H

és

F

képe egy

e

tengelyű és

k

-t egy

k'

körbe vivő (

k'

e

túlsó oldalán) merőleges affinitásban rendre

G'

H'

F'

; ezek egy, az

E

-n átmenő egyenesen vannak, mert egyenes affin képe egyenes. Másrészt

G G' ∥ H H' ∥ F F'

, mert merőlegesek

e

-re, így a párhuzamos szelők tétele alapján az

E G' : E G

, az

E H' : E H

és az

E F' : E F

arányok egyenlők, jelöljük közös értéküket

μ

-vel (2. ábr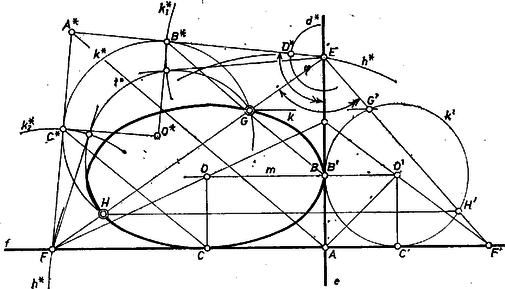a).

2. ábra

Ez azt jelenti, hogy a mondott affinitás inverzén túl ismerünk még egy olyan transzformációt, mely az

E

G'

H'

F'

pontokat rendre

E

-be,

G

-be,

H

-ba,

F

-be viszi vissza, éspedig az a forgatva nyújtás ez, melynek középpontja

E

, nyújtási arányszáma

μ

, elfordítási szöge pedig akkora és olyan irányú, amely az

E F'

félegyenest

E F

-be viszi át. (Ez a transzformáció

k'

további pontjait természetesen nem a

k

ellipszisbe viszi át, hiszen

k

más pontjaira az arányok értéke nem

μ

). És mivel

k'

átmegy

G'

-n és

H'

-n, továbbá az affinitás tulajdonságai alapján érinti

e

-t és

f

-et, vagyis a hozzá

E

-ből,

F'

-ből húzott érintők merőlegesen állnak egymásra, azért

k'

-nek a mondott forgatva nyújtással keletkező

k^{*}

képe a

G

-n és

H

-n átmenő kör, és a hozzá

E

-ből és

F

-ből húzott érintők merőlegesek egymásra. Ezek pedig azt jelentik, hogy

k^{*}

E

G

H

F

pontok ismeretében valóban megszerkeszthető a P. 39-beli eljárás szerint. Az ábrán

k^{*}

-ra csak egy megoldást tüntettünk föl, éspedig olyat, amelyre nézve ‐ az

E

-ből és

F

-ből húzott, egymásra merőleges

{E B}^{*}

{F C}^{*}

érintők metszéspontját

A^{*}

-gal jelölve ‐ az

E F A^{*}

derékszögű háromszög körüljárása ellentétes irányú az

E F A

derékszögű háromszög körüljárásával. A P.39-beli

t

k_{1}

k_{2}

h

d

körök és

D

pont megfelelője rendre

t^{*}

k_{1}^{*}

k_{2}^{*}

h^{*}

d^{*}

D^{*}

.
Ezek után a

k^{*}

-ból

k'

-t előállító forgatva nyújtásnak ‐ a fenti meggondolásbeli forgatva nyújtás inverzének ‐ szöge és arányszáma abból adódik, hogy az

{E A}^{*}

szakasz

E A

-ba jut át. Eszerint

B'

-t (ami azonos

B

-vel) kimetszi az

A^{*} A

-val párhuzamos,

B^{*}

-on átmenő egyenes,

O'

-t pedig a

B

-n át

e

-re állított

m

merőlegesből az

E A F

derékszög mellékszögének felezője.

F'

-t kijelöli az

A^{*} E A

és

F E F'

forgásszögek egyenlősége (az

A F

szakasz

A

-n túli meghosszabbításán), végül az

e

és

F' O'

közös pontját

F

-fel összekötő egyenesnek

m

-mel való, metszése

O

, és ennek

f

-en levő vetülete

C

. Így az

E A F'

háromszög körüljárása egyező az

E A^{*} F

háromszögével, tehát ellentétes az

E A F

háromszögével, amint a felhasznált affinitás kívánja.
A szerkesztés utóbbi része helyességének bizonyítását az olvasóra hagyjuk, a diszkusszió pedig természetesen azonos a P. 39-ben olvashatóval.

Megjegyzések. 1. A forgatva nyújtás és az affin leképezés eredményeképpen

F C^{*} : F A^{*} = F' C' : F' A = F C : F A

, ezért

C C^{*} ∥ A A^{*}

ami

B B^{*}

és

A A^{*}

föl is használt párhuzamos voltával együtt azt sejteti, hogy a ,,csillagos'' rendszer egyetlen transzformációval, ferde affinitással is átvihető a keresett ellipszis rendszerébe. Ennek teljes kivizsgálását is az érdeklődőkre hagyjuk.
2. Megoldható a feladat koordináta-geometriai számító előkészítéssel is.

¹A logikai sorrendnek megfelelően a

G'_{1}

jelet ezúttal így célszerű kiolvasni: (nagy) gé vessző egy.

²Lásd a megoldást K. M. L. 40 (1970) 74. o.