Kezdőlap


Feladat:	Pontversenyen kívüli P.51	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Boros Endre , Göndőcs Ferenc , Horváthy Péter , Komjáth Péter , Lempert László , Reviczky János , Waszlavik László
Füzet:	1970/október, 70 - 72. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Vetítések, Körülírt kör, Beírt kör, Húrnégyszögek, Síkgeometriai számítások trigonometria nélkül háromszögekben, Vektorok skaláris szorzata, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/december: Pontversenyen kívüli P.51

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C$ háromszög köré írt kör középpontja $K$ , a háromszögbe írt kör középpontja $O$ , a $K$ és $O$ pontoknak a vetülete a $B C$ egyenesen $A_{1}$ és $A_{2}$ , az $A C$ egyenesen $B_{1}$ és $B_{2}$ . Az $O$ -n át $B C$ -vel párhuzamosan húzott egyenes messe $A_{1} K$ -t $A_{3}$ ban, az $O$ -n átmenő, $A C$ -vel párhuzamos egyenesnek és $B_{1} K$ -nak a metszéspontja legyen 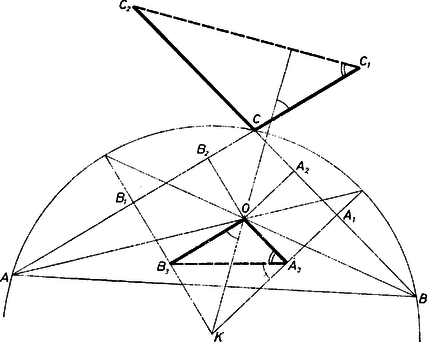$B_{3}$ .

1. ábra

A bizonyítást az 1. ábra viszonyaira fogjuk elmondani. Az

A_{3} O B_{3} K

négyszögben

A_{3}

-nál és

B_{3}

-nál derékszög van, ez tehát húrnégyszög. Megmutatjuk, hogy az

A C

egyenesnek az

O K

és

C_{1} C_{2}

egyenesekkel alkotott szögeinek összege egyenlő az

O A_{3} K

szöggel; ezzel feladatunk állítását bebizonyítjuk, hiszen ez utóbbi derékszög.

A C

és

O K

szöge egyenlő a

B_{3} O K

szöggel, hiszen

B_{3} O | | A C

. A

B_{3} O K

szög egyenlő a

B_{3} A_{3} K

szöggel, mert

A_{3} O B_{3} K

húrnégyszög. Elegendő tehát megmutatni, hogy a

C C_{1} C_{2}

és

O A_{3} B_{3}

háromszögek hasonlóak. E két háromszög

C

, illetve

O

csúcsra támaszkodó oldalai párhuzamosak, megmutatjuk, hogy az arányuk is megegyezik. A feladat szerint

C C_{1} = c - b

. Ismeretes, hogy

C A_{2} = s - c

, emiatt

\begin{matrix} O A_{3} = A_{2} A_{1} = C A_{1} - C A_{2} = \frac{a}{2} - (s - c) = \frac{c - b}{2} . \end{matrix}

Tehát

C C_{1} : O A_{3} = 2 : 1

, és hasonlóan kapjuk, hogy

C C_{2} : O B_{3} = 2 : 1

Megjegyzések. 1. Az

O

és

K

középpontok akkor és csak akkor esnek egybe, ha a háromszög szabályos, akkor viszont

C_{1}

és

C_{2}

is egybeesik. Így a feladat állítása értelmét veszti.
2. Nem nehéz megfelelően módosítani a bizonyítást az ábrán láthatótól különböző elhelyezkedés esetén sem, vagy belátni, hogy állításaink érvényesek tetszőleges háromszögre, ha az előforduló szögeket és szakaszokat irányított mennyiségeknek tekintjük. Elkerülhetjük azonban a diszkusszióval járó nehézségeket vektorok használatával is.

II. megoldás. A

C_{1} C_{2}

vektor az egyenlő abszolút értékű

C_{1} A

A B

B C_{2}

vektorok összegével egyenlő, e vektorok iránya pedig rendre az

A B C

háromszög megfelelő oldalvektorának az irányával egyezik meg.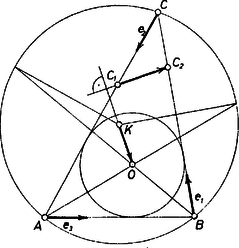

2. ábra

Elegendő tehát megmutatni, hogy (2. ábra):

\begin{matrix} O K ⊥ (e_{1} + e_{2} + e_{3}), \end{matrix}

ahol

e_{1}

e_{2}

e_{3}

B C

C A

A B

oldalvektorokkal megegyező irányú egységvektorok. Vektorok skaláris szorzatát felhasználva ezt a következő módon láthatjuk be. Legyen az

A

B

C

O

pontokhoz a

K

centrumból húzott helyvektor rendre

a

b

c

p

, akkor

\begin{matrix} (p - a) (e_{2} + e_{3}) = 0, \\ (p - b) (e_{3} + e_{1}) = 0, \\ (p - c) (e_{1} + e_{2}) = 0, \end{matrix}

hiszen pl. az

A O

egyenes merőleges minden olyan egyenlő szárú háromszög alapjára, melynek szárai egyirányúak az

A C

A B

oldalakkal. Összefüggéseinket összeadva kapjuk, hogy

\begin{matrix} 2 p (e_{1} + e_{2} + e_{3}) - [(a + b) e_{3} + (b + c) e_{1} + (c + a) e_{2}] = 0. \end{matrix}

Itt a második tag 0, mert pl. az

(a + b))

vektor merőleges

A B

-re, így

(a + b) e_{3} =

= 0

, és hasonló módon

(b + c) e_{1} = 0

(c + a) e_{2} = 0

. Így

\begin{matrix} p (e_{1} + c_{2} + e_{3}) = 0, \end{matrix}

amint azt bizonyítanunk kellett.

Lempert László

Megjegyzések. 1. Könnyen belátható a következő állítás: egységnek a háromszög köré írt kör sugarát véve, a

K

-ból induló és az oldalakra, merőlegesen álló három egységvektor összege éppen a

\vec{K O}

vektor (3. ábra, a vektorok irányítása: mindegyik csúcstól a szemben levő oldal felé).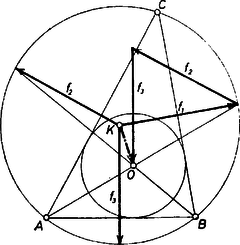

3. ábra

Ha pedig két vektor irányítását ellentétesre fordítjuk, az összegvektor végpontja a harmadik oldalhoz hozzáírt érintő kör középpontjában lesz.
2. Utóbbi megoldásunkból kiolvasható a következő egyszerű állítás bizonyítása is. Legyen

A B C D

egyenlő szárú trapéz. Emeljünk merőlegest az

A D

szár végpontjaiban az oda befutó átlókra, ezek metszéspontja legyen

Q

P

pedig legyen az átlók metszéspontja. Akkor

P Q

merőleges

B C

-re (4. áb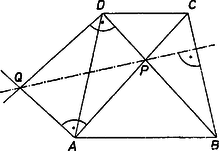ra).

4. ábra