|
| Feladat: |
Pontversenyen kívüli P.50 |
Korcsoport: 16-17 |
Nehézségi fok: nehéz |
| Megoldó(k): |
Csuka G. , Ferró J. , Frankl P. , Füredi Z. , Földvári Cs. , Gál P. , Göndöcs F. , Hovárhty P. , Iván L. , Kirchner I. , Komjáth P. , Komócsi S. , Lakatos B. , Lempert L. , Lipécz Gy. , Nagy F. , Nyilánszky M. , Papp Z. , Prőhle T. , Simonyi Gyula , Szabó György , Vajnági András , Váradi Judit , Waszlavik L. , Wittmann I. |
| Füzet: |
1970/május,
217 - 218. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Kombinatorika, Teljes indukció módszere, Pontversenyen kívüli probléma |
| Hivatkozás(ok): | Feladatok: 1969/december: Pontversenyen kívüli P.50 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Pingpongmérkőzés nem végződhet döntetlenül, így két résztvevős ,,körmérkőzés'' esetére az állítás nyilvánvalóan igaz. Erre támaszkodva, helyességét (a résztvevők száma szerinti) teljes indukcióval bizonyítjuk: feltesszük, hogy az állítás helyes, ha a résztvevők száma legföljebb .
résztvevő esetén szemeljük ki egyiküket, legyen ez . A többi játékos feltevésünk szerint sorba állítható a kívánt módon az egymás közt lejátszott mérkőzések alapján. Állítsuk most -t ebbe a sorba az első olyan elé, akit ő legyőzött ‐ amennyiben ilyen van ‐, különben a sor végére. Így helyzete nemcsak a hátsó, hanem elülső szomszédjához viszonyítva is megfelelő, hiszen az előtte állók egyikét sem győzte le, tehát vagy az áll, hogy azok mind legyőzték -t, vagy pedig senki sem győzte le, akkor pedig őt az első helyre állítottuk. ilyen beállítása sem az előtte, sem a mögötte állók egymás közti elhelyezését nem változtatta meg, így az játékos megfelelő sorbaállítására példát adtunk. Ezzel bizonyításunkat befejeztük.
| Váradi Judit (Budapest, Berzsenyi D. Gimn., IV. o. t.) |
Megjegyzések. 1. Lényegében ugyanígy okoskodhatunk -t az utolsó olyan játékostársa után állítva be, aki még őt legyőzte; ha pedig ilyen nincs, akkor természetesen az első helyre.
| Simonyi Gyula (Székesfehérvár, Teleki Blanka Gimn., III. o. t.) |
2. Egy játékos ‐ ismét ‐ kiemelése után a többi résztvevőt két csoportba osztjuk: legyőzőinek és a által legyőzötteknek csoportjára. Egyik csoport létszáma sem nagyobb -nél, így mindegyik csoport külön-külön megfelelően sorba állítható a feltevés értelmében. Végül -t az I. csoport utolsó tagja után állítjuk, utána pedig a II. csoportot a mondott sorrendben.
II. megoldás. Állítsuk sorba találomra a versenyzőket, majd az első kettőt cseréljük fel, ha az első kikapott a másodiktól, különben hagyjuk őket az eredeti sorrendben, majd sorra a másodikat és harmadikat, harmadikat és negyediket, és így tovább, cseréljük meg, ha nem megfelelő sorrendben állnak. Előfordulhat, hogy így egy cserével az előbbre került versenyző és az előtte álló közt helytelen sorrend keletkezik, ezért a sor végére érve térjünk vissza az elejére és ismételjük meg újra és újra az eljárást.
Belátjuk, hogy véges sokszor végighaladva a soron, eljutunk egy olyan elrendezéshez, amely már kielégíti a feladat követelményeit. Valóban a versenyzők csak véges számú különböző sorrendben állhatnak, így elég sokszor végigmenve a soron, elő kell fordulnia egy olyan sorrendnek, amelyik már korábban is előfordult. Ez azonban csak akkor lehetséges, ha végighaladva már nincs szükség cserére, azaz ha a sorrend kielégíti a feladat feltételeit. Ha ugyanis valakit felcseréltünk a rákövetkezővel, az minden későbbi sorrendben is hátrább marad nála, hiszen őket ellenkező irányban nem cserélhetjük meg, így a korábbi sorrend nem térhet vissza.
Megjegyzések. 1. Lényegesen kihasználtuk, hogy minden játékos játszott mindenkivel. E nélkül a feladat állítása nem igaz. Ha ugyanis pl. egyetlen pár játszmája elmaradt és ez a két játékos minden további résztvevőtől kikapott (vagy mindenkit megvert), akkor e két játékos közül egyik sem előzheti meg a másikat, a kívánt felállítás lehetetlen.
2. Állításunk ekvivalens azzal, hogy ha egy a szögpontú teljes gráf éleit akárhogy is irányítjuk, mindig létezik egy olyan élsorozat, melyen végighaladva minden szögponton egyszer megyünk át, és amelyben a nyilak irányítása végig azonos. (Ilyen utat a gráfelméletben Hamilton-vonalnak neveznek.) E tényt először Kőnig Dénes (1884‐1944) bizonyította be. Hasonló gráfelméleti tételeit sikeresen alkalmazzák napjaink gazdasági-programozási feladatainak megoldásában.
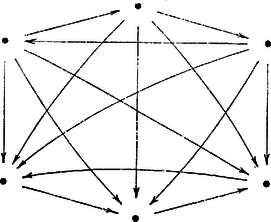
3. Ahhoz, hogy a résztvevőket a kívánt módon körbe is lehessen állítani, szükséges, hogy ne legyen olyan játékos, aki mindenkit megvert, vagy mindenkitől kikapott. E feltétel teljesülése azonban nem elégséges, mint azt az ábrán bemutatott gráf mutatja.
Természetesen úgy értjük a kérdést, hogy mindenki mindenkivel egyszer játszott. |
|
 PDF |
PDF |  MathML
MathML