Kezdőlap


Feladat:	Pontversenyen kívüli P.48	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Füredi Zoltán , Göndőcs Ferenc , Lempert László , Nagy Ferenc , Papp Zoltán , Vajnági András
Füzet:	1970/április, 169 - 171. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Húrnégyszögek, Periodikus sorozatok, Számhármasok, Szabályos sokszögek geometriája, Alakzatok köré írt kör, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/november: Pontversenyen kívüli P.48

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vizsgáljunk egy $K_{n}$ szabályos $n$ -szöget, jelölje $k_{n}$ a körülírt körét, $O$ ennek középpontját, $A$ , $B$ , $C$ pedig $K_{n}$ három különböző csúcsát. Jelölje továbbá $H_{0}$ az $A B C$ háromszöget és legyen $H_{k + 1}$ a $H_{k}$ háromszög talpponti háromszöge ( $k = 0,1,2, ...$ ). Keressük annak feltételét, hogy a $H_{1}$ , $H_{2}, ...$ sorozatban legyen a $H_{0}$ -hoz hasonló háromszög.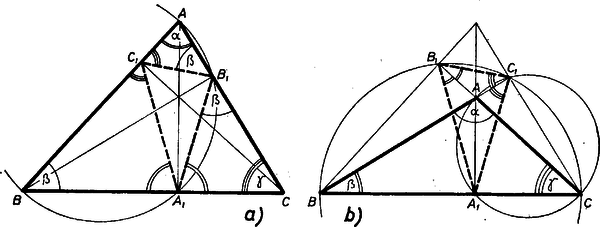
Ha egy háromszög szögei $α$ , $β$ , $γ$ , és ezek mindegyike hegyesszög, akkor a talpponti háromszög szögei rendre $180^{\circ} - 2 α$ , $180^{\circ} - 2 β$ , $180^{\circ} - 2 γ$ , (lásd 1a) ábra: $C B_{1} A_{1} ∢ = β$ , mert $A_{1} B A B_{1}$ húrnégyszög stb.). Ha a háromszög derékszögű, akkor a talpponti háromszög nem létezik. Tompaszögű háromszögben, ha $α > 90^{\circ}$ , akkor a talpponti háromszög szögei $2 α - 180^{\circ}$ , $2 β$ , $2 γ$ (lásd 1b) ábra: $A C_{1} A_{1} ∢ = γ$ , mert $A C_{1} C A_{1}$ húrnégyszög stb.).

1. ábra

K_{n}

egy oldalán nyugvó középponti szög

360^{\circ} / n

, így

K_{n}

bármely két csúcsa közti íven nyugvó kerületi szög az

ε = 180^{\circ} / n

egész számú többszöröse. Ez azt jelenti, hogy alkalmas

i

j

k

pozitív egész számok mellett

H_{0}

szögei

\begin{matrix} i ε, j ε, k ε, ahol i + j + k = n . \end{matrix}

Ekkor

H_{1}

szögeit a fentiek szerint a következő 4 képlethármas valamelyike adja:

\begin{matrix} (n - 2 i) ε, (n - 2 j) ε (n - 2 k) ε; (2 i - n) ε, 2 j ε,2 k ε; 2 i ε, (2 j - n) ε, 2 k ε; \end{matrix}

\begin{matrix} 2 i ε, 2 j ε, (2 k - n) ε . \end{matrix}

Mindegyikben

ε

együtthatóinak összege

n

. És mivel bárhogy választva az

i + j + k = n

feltételt kielégítő pozitív egész számokat, létezik

K_{n}

-nek olyan három csúcsa (ha ti.

K_{n}

egymás utáni csúcsai

D_{0}, D_{1}, ..., D_{n - 1}

, akkor pl.

D_{0}

D_{2 i}

és

D_{2 i + 2 j}

), hogy az általuk meghatározott háromszög szögei éppen

i ε, j ε, k ε,

azért a

H_{1}, H_{2}, ...

sorozat minden háromszöge hasonló a

K_{n}

-ből kiválasztható háromszögek valamelyikéhez.
Legyen

r

az a legnagyobb kitevő, amelyre

2^{r}

még osztója

n

-nek; azaz

n = 2^{r} \cdot m

, ahol

m

páratlan. Megmutatjuk, hogy

(F)

: a

H_{1}

H_{2} ...

sorozatban akkor és csak akkor van

H_{0}

-hoz hasonló háromszög, ha

2^{r}

i

j

k

számok mindegyikének osztója.(Derékszögű háromszögre a feltétel nem teljesülhet, hiszen abban pl.

i = j + k = n / 2

, és ez 2-nek 1-gyel alacsonyabb hatványával osztható, mint

n

.)
Legyen pl.

i = 2^{δ} \cdot μ

, ahol

δ

μ

egészek,

δ \geq 0

és

μ

páratlan. Ekkor

H_{1}

megfelelő szögében, ami

\begin{matrix} (n - 2 i) ε vagy (2 i - n) ε vagy 2 i ε, \end{matrix}

ε

együtthatója

δ < r

esetén osztható

2^{δ + 1}

-nel,

δ \geq r

esetén pedig

2^{r}

-nel. Ez azt jelenti, hogy amennyiben

2^{r}

nem osztója

i

j

k

mindegyikének, akkor

H_{0}

-nak van olyan szöge, amelytől a

H_{1}, H_{2}, ...

sorozat minden szöge különbözik; feltételünk tehát szükséges.
Eszerint ha

n = 2^{r} \cdot m

, akkor a

K_{n}

sokszög kerületének a

H_{0}

bármelyik két csúcsa közti részén az oldalak száma

2^{r}

-nek egész többszöröse, így

H_{0}

csúcsai kiválaszthatók annak a

k_{n}

-be írt

K_{m}

szabályos

m

-szögnek a csúcsai közül is, amelyiknek egyik csúcsa

A

. Elegendő tehát a továbbiakban páratlan

n

esetét vizsgálni.
Megmutatjuk, hogy tetszőleges (a

K_{n}

-ből választott, ahol

n

páratlan)

H

háromszöghöz egy és csakis egy

H^{*}

háromszög tartozik, melynek talpponti háromszöge hasonló

H

-hoz. Ebből már következik, hogy a fenti feltétel elegendő is, hiszen a választható háromszögek száma véges, tehát bármelyikükből kiindulva periodikus sorozatot kapunk, és ha ez a sorozat nem már az elejétől volna periodikus, akkor az a háromszög, mely az első periódus első eleme, két különböző háromszögből származna.
Legyenek a

H

háromszög szögei

i' ε, j' ε, k' ε, (i' + j' + k' = n)

és legyen az

i^{*} ε, j^{*} ε,, k^{*} ε

szögekkel bíró

H^{*}

háromszög talpponti háromszöge hasonló

H

-hoz. Ekkor az

i', j', k'

számhármas valamilyen sorrendben azonos az

\begin{matrix} n - 2 i^{*} & n - 2 j^{*}, & n - 2 k^{*}, & (1) \\ 2 i^{*} - n, & 2 j^{*}, & 2 k^{*}, & (2) \\ 2 i^{*}, & 2 j^{*} - n, & 2 k^{*}, & (3) \\ 2 i^{*}, & 2 j^{*}, & 2 k^{*} - n & (4) \end{matrix}

számhármasok valamelyikével. (1)-ben három páratlan szám áll, (2)‐(4)-ben pedig egy-egy, eszerint ha

i'

j'

k'

mindegyike páratlan, akkor

H^{*}

szögei (1) alapján határozhatók meg egyértelműen, pl.

i^{*} = (n - i') / 2

, ha pedig

i'

j'

k'

közül csak egy páratlan, akkor (2) alapján (hiszen

i^{*}

j^{*}

k^{*}

sorrendje nem lényeges), pl. ha

i'

páratlan,

j'

és

k'

pedig páros, akkor

i^{*} = (n + i') (2, j^{*} = j' / 2

. Ezzel

F

állításunkat bebizonyítottuk.
Mivel pedig

a = 2^{r} m

-ben

r > 0

esetén választható olyan

H_{0}

, melyben

i

páratlan, a kérdező sejtése páros oldalszámú szabályos sokszögre nem igaz. Páratlan oldalszám esetén viszont mindig igaz.

Göndőcs Ferenc, Füredi Zoltán