Kezdőlap


Feladat:	Pontversenyen kívüli P.47	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Donga György , Göndőcs Ferenc , Lempert László
Füzet:	1970/április, 167 - 169. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül körökben, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/november: Pontversenyen kívüli P.47

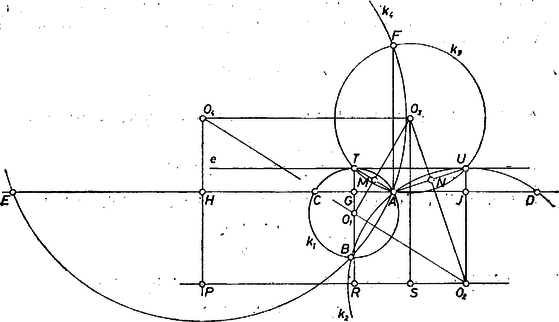
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a kiindulási köröket $k_{1}$ -gyel és $k_{2}$ -vel és húzzuk meg egyik közös érintőjüket, $e$ -t. Egyértelműség kedvéért legyen $A$ a körök $e$ -hez közelebbi metszéspontja. A $T$ és $U$ , ill. az ennek megfelelő $C$ és $D$ jelölést úgy válasszuk meg, hogy $C A < A D$ teljesüljön. (Ha $C A = A D$ , akkor a kívánt $E$ pont nem létezik, s így a feladat értelmét veszti.) Az általánosság megszorítása nélkül feltehetjük, hogy $C$ a $k_{1}$ körön van. Ha $C A < A D$ akkor az $E$ pont egyértelműen meghatározott, $A C$ -nek a $C$ -n túli meghosszabbításán van. Vezessük be még a következő jelöléseket: jelölje $k_{3}$ , ill. $k_{4}$ az $A$ , $T$ , $U$ pontokon, ill. az $A$ , $B$ , $E$ pontokon átmenő kört, s legyen $O_{i}$ a $k_{i}$ kör középpontja ( $i$ =1, 2, 3, 4), $J$ , $G$ , $H$ , $M$ , $N$ pedig rendre az $A D$ , $A C$ , $A E$ , $A T$ , $A U$ szakasz felezőpontja. Vegyük észre, hogy $O_{2}$ távolabb van $e$ -től, mint $O_{1}$ , továbbá azt, hogy az $O_{1} T$ egyenesnek két különböző oldalán van $O_{3}$ és $O_{4}$ .

A F

egyenes a

k_{3}

és

k_{4}

körök közös húrja, ezért merőleges a középpontjaikat összekötő egyenesre. Ezért azt bizonyítjuk, hogy az

O_{3} O_{4}

egyenes párhuzamos

e

-vel. E célból húzzunk párhuzamost

e

-vel

O_{2}

-n át, s jelöljük

P

R

S

betűvel az

O_{4}

O_{1}

O_{3}

pont merőleges vetületét ezen az egyenesen. Mivel

O_{4} P

és

O_{3} S

párhuzamosak, így állításunk helyességéhez elegendő egyenlőségüket bizonyítani. A következőkben ezt fogjuk megtenni.
Mindenekelőtt állapítsuk meg a következőket:

\begin{matrix} P O_{2} = H J = \frac{1}{2} E D \end{matrix}

(1)

és

\begin{matrix} R O_{2} = G J = \frac{1}{2} C D = 2 S O_{2} . \end{matrix}

(2)

O_{3} S O_{2}

háromszög és

A J U

háromszög hasonlóak, hiszen az

S

-nél, ill.

J

-nél levő szögeik derékszögek, míg az

O_{3}

-nál és

A

-nál levő szögek merőleges szárú szögek. Így

\begin{matrix} O_{3} S = O_{2} S \cdot \frac{A J}{U J} . \end{matrix}

(3)

A J U

háromszög és

O_{2} N U

háromszög ugyancsak hasonlóak, így

\begin{matrix} O_{2} U = \frac{N U \cdot A U}{U J} = \frac{A U^{2}}{2 \cdot U J} . \end{matrix}

(4)

Ugyanígy az

O_{4} P O_{2}

háromszög és

O_{1} R O_{2}

háromszög hasonlósága miatt

\begin{matrix} O_{4} P = \frac{O_{1} R \cdot P O_{2}}{R O_{2}}, \end{matrix}

(5)

míg az

O_{1} M T

háromszög és

A G T

háromszög hasonlósága miatt

\begin{matrix} O_{1} T = \frac{A T^{2}}{2 G T} = \frac{A T^{2}}{2 U J} . \end{matrix}

(6)

C

(és így

O_{2}

) elnevezése miatt

\begin{matrix} R O_{1} = R T - O_{1} T = O_{2} U - O_{1} T, \end{matrix}

(4) és (6) segítségével ebből

\begin{matrix} O_{1} R = \frac{A U^{2} - A T^{2}}{2 U J} = \frac{(A U^{2} - U J^{2}) - (A T^{2} - U J^{2})}{2 U J} = \\ \frac{A J^{2} - A G^{2}}{2 U J} = \frac{A J - A G}{U J} \cdot \frac{A J + A G}{2}, \end{matrix}

azaz

\begin{matrix} O_{1} R = \frac{(A J - A G) O_{2} S}{U J} . \end{matrix}

(7)

Végül

E

definíciója miatt:

\begin{matrix} \frac{E D - C D}{E D} = \frac{A C}{A D}, \end{matrix}

ahonnan

\begin{matrix} E D = \frac{C D \cdot A D}{A D - A C} . \end{matrix}

(8)

Mármost (1), (2), (7) és (8) segítségével (5) így alakítható át:

\begin{matrix} O_{4} P = \frac{(A J - A G) O_{2} S}{U J} \cdot \frac{1}{2} \cdot \frac{C D \cdot A D}{A D - A C} \cdot \frac{1}{2 S O_{2}} . \end{matrix}

Mivel pedig

\begin{matrix} \frac{A J - A G}{A D - A C} = \frac{1}{2}, \end{matrix}

azért (3) alapján

\begin{matrix} O_{4} P = \frac{C D \cdot A D}{8 U J} = \frac{C D}{4} \cdot \frac{\frac{A D}{2}}{U J} = O_{2} S \cdot \frac{A J}{U J} = O_{3} S, \end{matrix}

ami bizonyítandó volt. Hasonlóan bizonyítható az állítás akkor is, ha

A

szerepét az

e

-től távolabbi metszéspont játssza. (Ha előjeles távolságokkal dolgozunk, nincs szükség erre a megkülönböztetésre.)

Donga György (Budapest, Berzsenyi D. Gimn., III. o. t.)

Megjegyzés. A bizonyítás elvégezhető valamely az

A

körüli körre vonatkozó inverz alakzatokra való áttéréssel is.