Kezdőlap


Feladat:	Pontversenyen kívüli P.45	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Barabás E. , Donga György , Füredi Zoltán , Göndőcs Ferenc , Lempert László , Martoni Viktor , Pál Jenő , Papp Zoltán , Petz Dénes , Simonyi Gy.
Füzet:	1970/május, 214 - 216. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Gyökök és együtthatók közötti összefüggések, Egész együtthatós polinomok, Számsorozatok, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/november: Pontversenyen kívüli P.45

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Először $a$ -t fejezzük ki az

\begin{matrix} a + a^{- 1} = a + \frac{1}{a} = A, \end{matrix}

másképpen

a^{2} - A a + 1 = 0

egyenletből. A két gyök szorzata

1

, így

\begin{matrix} a_{1} = \frac{A + \sqrt[]{A^{2} - 4}}{2}, a_{2} = \frac{1}{a_{1}}, \end{matrix}

és ezek csak egy értéket adnak

A_{n}

céljára, hiszen

\begin{matrix} a_{1}^{n} + \frac{1}{a_{1}^{n}} = \frac{1}{a_{2}^{n}} + a_{2}^{n}, \end{matrix}

éspedig

\begin{matrix} A_{n} = \frac{1}{2^{n}} {{(A + \sqrt[]{A^{2} - 4})}^{n} + {(A - \sqrt[]{A^{2} - 4})}^{n}} . \end{matrix}

(1)

A kapott kifejezés

A

-nak polinomja, mert a két

n

-edik hatvány kifejtése csak a négyzetgyökös kifejezés páratlan kitevős hatványainak előjelében különbözik, ezek összege pedig megfelelő páronként

0

.
A legutóbbi megállapításban csak pozitív egész

n

-ekre gondoltunk. Minthogy azonban ‐ az

n

-nel tovább is pozitív egész számot jelölve ‐ fennáll

A_{- n} = A_{n}

, továbbá

n = 0

esetén minden

a

-ra

A_{0} = 2

(hacsak

a \neq 0

), és ezt (1) is kiadja, azért (1) minden egész

n

-re érvényes.
Adott

A

esetében

a

és

A_{n}

akkor valós, ha

| A | \geq 2

. További elemzéstől eltekintünk.

Petz Dénes (Budapest, Veres Pálné Gimn., III. o. t.)

II. megoldás. Problémánk kapcsolatban van az 1234. gyakorlattal,^{$^{*}$} ott

A_{n}

-et a

2 \leq n \leq 7

értékekre állítottuk elő. Ottani eredményeinket kissé átalakítva, az

n = 0

1

esetekkel kiegészítve és növekvő hatványok szerint rendezve az 1. ábra sémájában foglaljuk össze.

1. ábra

Ezekre az értékekre

A_{n}

-et

A

polinomjának találtuk, mindegyikben csak az

n

-nel egyező párosságú kitevők lépnek fel.
Lényegében már az ottani előállításban felhasználtuk az

\begin{matrix} A_{n + 1} = A \cdot A_{n} - A_{n - 1} \end{matrix}

rekurziót, amelyet

A_{n}

definíciója alapján könnyen igazolhatunk:

\begin{matrix} a^{n + 1} + \frac{1}{a^{n + 1}} = (a + \frac{1}{a}) (a^{n} + \frac{1}{a^{n}}) - (a^{n - 1} + \frac{1}{a^{n - 1}}), \end{matrix}

ez a kitevők párosságáról mondottaknak bármely

n

-re való érvényességét is bizonyítja. Ennek alapján

A_{n + 1}

polinom-alakjában minden egyes együtthatót az 1. ábrabeli séma megfelelő helyén úgy állíthatunk elő, hogy a balra fölötte levő együtthatóból kivonjuk a két sorral fölötte levő együtthatót ‐ amint ezt a séma vastag nyilai mutatják.
Azt látjuk, és könnyen igazolható általában, hogy az előjel minden egyes oszlopban lépésről lépésre változik, a jobbra (

45^{\circ}

-os szöggel) lejtő egyenesek mentén viszont állandó. Ezt tudva minden egyes együttható abszolút értékét a balra fölötte és két sorral fölötte álló együttható összege adja.

Papp Zoltán, Göndős Ferenc

Megjegyzések. 1. Az együtthatók abszolút értékére talált előállítás emlékeztet a Pascal-háromszög képezési szabályára. Az elhelyezés szerint is meglesz a megfelelés, ha sémánkat átrendezzük, a balra (

45^{\circ}

szöggel) lejtő egymás utáni egyeneseken levő együtthatókat írjuk egy új séma egymás utáni soraiba (2. ábra).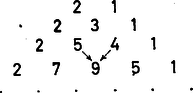

2. ábra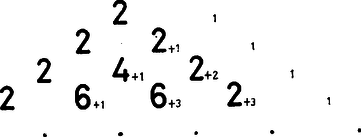

3. ábra

Ezt a sémát ‐ ha belső tagjait a 3. ábra szerint összegekre bontjuk ‐ két háromszög-séma összegének tekinthetjük, a jobb oldali (kisebb számjegyekkel írt) séma maga a Pascal-háromszög, balra

1

hellyel eltolva (nagyobb számjegyekkel írva) pedig a

2

-szeresét látjuk.
Az

A_{n}

polinom-alakjában fellépő együtthatókat tehát egy binomiális együttható kétszeresének és a rá következő együtthatónak összegeként állíthatjuk elő. Így pl.

\begin{matrix} A_{7} = - [2 \cdot (\binom{3}{2}) + (\binom{3}{3})] A + [2 \cdot (\binom{4}{1}) + (\binom{4}{2})] A^{3} - [2 \cdot (\binom{5}{0}) + (\binom{5}{1})] A^{5} + (\binom{6}{0}) A^{7} . \end{matrix}

Innen leolvashatjuk az általános alakot (célszerűbben a tagok fordított sorrendjében felírva):

\begin{matrix} A_{n} = (\binom{n - 1}{0}) A^{n} - [2 \cdot (\binom{n - 2}{0}) + (\binom{n - 2}{1})] A^{n - 2} + ... + {(- 1)}^{k} [2 \cdot (\binom{n - k - 1}{k - 1}) + \\ + (\binom{n - k - 1}{k})] A^{n - 2 k} + ... \end{matrix}

Az így előállított összefüggést ugyan a fenti meggondolással is bizonyíthatnánk, mégis kényelmesebb közvetlenül, teljes indukcióval bizonyítani: a fenti rekurzió alapján:

\begin{matrix} A_{n + 1} = A A_{n} - A_{n - 1} = A \cdot \sum_{k = 0} {(- 1)}^{k} [2 \cdot (\binom{n - k - 1}{k - 1}) + (\binom{n - k - 1}{k})] A^{n - 2 k} - \\ - \sum_{j = 0} {(- 1)}^{j} [2 \cdot (\binom{n - 1 - j - 1}{j - 1}) + (\binom{n - 1 - j - 1}{j})] A^{n - 1 - 2 j} = \\ = \sum_{k = 0} {(- 1)}^{k} {2 [(\binom{n - k - 1}{k - 1}) + (\binom{n - k - 1}{k - 2})] + [(\binom{n - k - 1}{k}) + (\binom{n - k - 1}{k - 1})]} A^{n + 1 - 2 k} = \\ = \sum_{k = 0} {(- 1)}^{k} [2 (\binom{n + 1 - k - 1}{k - 1}) + (\binom{n + 1 - k - 1}{k})] A^{n + 1 - 2 k} . \end{matrix}

Az egyes együtthatókban szereplő binomiális együtthatókat össze is vonhatjuk:

\begin{matrix} 2 (\binom{n - k - 1}{k - 1}) + (\binom{n - k - 1}{k}) = (\binom{n - k - 1}{k - 1}) [2 + \frac{n - 2 k}{k}] = \frac{n}{k} (\binom{n - k - 1}{k - 1}), \end{matrix}

tehát

\begin{matrix} A_{n} = \sum_{k = 0}^{[\frac{n}{2}]} {(- 1)}^{k} \frac{n}{k} (\binom{n - k - 1}{k - 1}) A^{n - 2 k} . \end{matrix}

4. ábra

2. Értelmezhetjük a 2. ábrát a 4. ábra szerint is, a nagy számjegyekkel írt összetevő balra és lefelé 1 ‐ 1 hellyel való eltolással áll elő a másikból.

^{$^{*}$}K. M. L. 39 (1969) 59. o.