Kezdőlap


Feladat:	Pontversenyen kívüli P.44	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Füredi Zoltán , Földvári Csongor , Göndőcs Ferenc , Lempert László , Pataki Béla , Reviczky János
Füzet:	1970/április, 163 - 165. oldal		PDF \| MathML
Témakör(ök):	Inverzió, Diszkusszió, Síkgeometriai szerkesztések, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/október: Pontversenyen kívüli P.44

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fel fogjuk használni, hogy egy $P$ ponton és az $r$ sugarú, $O$ középpontú $k_{0}$ körre vonatkozó $P_{1}$ inverzén átmenő bármelyik $k^{*}$ kör merőlegesen metszi $k_{0}$ -t, és hogy $k^{*}$ bármely pontjának az inverz képét az őt $O$ -val összekötő egyenes metszi ki $k^{*}$ -ból. (Ha ez az egyenes érintő, akkor a pont a saját inverz képe.) Valóban $O P \cdot O P_{1} = r^{2}$ , tehát $k^{*}$ bármely $P^{*}$ pontjára és $O P^{*}$ -nak $k^{*}$ -gal való $P_{1}^{*}$ második metszéspontjára $O P^{*} \cdot O P_{1}^{*} = O P \cdot O P_{1} = r^{2}$ , s igy $P^{*}$ és $P_{1}^{*}$ egymás inverz képei; az $O$ -ból $k^{*}$ -hoz húzott érintők hossza pedig $r$ , vagyis az érintési pontok $k_{0}$ és $k^{*}$ metszéspontjai, a két kör ide húzott sugarai eszerint merőlegesek, vagyis a két kör merőlegesen metszi egymást (1. ábra).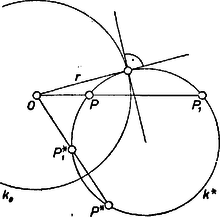

1. ábra

Jelöljük a háromszög csúcsait

A

B

C

-vel. Először megmutatjuk, hogy a keresett

P

pontból származó

P_{1}

P_{2}

P_{3}

pontok nem eshetnek egy egyenesbe. A

P_{i}

pontok definíciója szerint ugyanis az

A

P

P_{1}

, a

B

P_{1}

P_{2}

és a

C

P_{2}

P_{3}

ponthármas egy-egy egyenesen van, így ha

P_{1}

P_{2}

P_{3} = P

egy egyenesen volna, akkor ugyanerre az egyenesre esnék

A

B

C

is, ami lehetetlen. Létezik tehát a

P_{1}

P_{2}

P_{3}

pontok köré írt kör, jelöljük

k

-val, középpontját

O

-val. A

k

kör a bevezető megjegyzés szerint merőleges a

k_{1}

k_{2}

k_{3}

körök mindegyikére.
Mivel

k_{1}

k_{2}

k_{3}

sugara egyenlő, azért

O

egyenlő távolságra van az

A

B

C

pontok mindegyikétől, tehát

O

megegyezik az

A B C

háromszög centrumával. Ez módot ad a

k

kör megszerkesztésére: mivel a

k

-hoz, ill.

k_{1}

-hez metszéspontjukban húzott érintők merőlegesek egymásra és átmennek az

A

, ill.

O

ponton, így az

A O

szakasz

k_{4}

Thalész-körének és

k_{1}

-nek

D_{1}

és

D_{2}

metszéspontjai rajta vannak

k

-n is. Ezért

k

sugara egyenlő

O D_{1}

-gyel. Ilyen

k

kör tehát akkor és csak akkor létezik, ha

k_{1}

sugara

r \leq O A

(egyenlőség esetén

k

pontkör). Ez egyben a feladat megoldhatóságának is a feltétele, ezért a továbbiakban feltesszük, hogy

r < A O

. (Az

r = A O

eset triviális, ekkor

P

és képei azonosak

O

-val.)
Az, hogy az

A B C

háromszög szabályos, és hogy a

k_{1}

k_{2}

k_{3}

körök sugara egyenlő, azt sugallja, hogy a

P P_{1} P_{2}

háromszög is szabályos. Keressünk ezért ilyen megoldást. Vegyünk fel egy tetszőleges

P' P'_{1} P'_{2}

szabályos háromszöget

k

-ban (körüljárása egyezzék

A B C

-ével), hosszabbítsuk meg

P' P'_{1}

P'_{1} P'_{2}

P'_{2} P'

oldalát

P'_{1}

-en,

P'_{2}

- n, ill.

P'

-n túl és jelöljük e félegyeneseknek az

A B C

háromszög köré írható

k'

körrel vett metszéspontjait rendre

A'

B'

, ill.

C'

-vel. A

120^{\circ}

-os forgási szimmetria miatt az

A' B' C'

háromszög szabályos, létezik tehát olyan elforgatás, amely ezt az

A B C

háromszögbe viszi át. Vigye át ugyanez az elforgatás a

P' P'_{1} P'_{2}

háromszöget a

P P_{1} P_{2}

háromszögbe.
Az így nyert

P

pont egy megoldása feladatunknak, ugyanis

P

P_{1}

A

egy egyenesen vannak (

P A > P_{1} A

), s így a fenti megjegyzés szerint

P_{1}

P

pont

k_{1}

-re való inverze, hasonlóan

P_{2}

P_{1}

inverze

k_{2}

-re, és

P

P_{2}

pont

k_{3}

-ra vonatkozó inverze.
Ugyancsak megoldás az a

Q

Q_{1}

Q_{2}

ponthármas is, amely a

P'

P'_{1}

P'_{2}

hármasnak az az elforgatása, hogy

Q Q_{1}

-nek

Q

-n túli meghosszabbítása megy át

A

-n (így

Q A < Q_{1} A

Q_{1} Q_{2}

-nek

Q_{1}

-en túli meghosszabbítása

B

-n és

Q_{2} Q

-nak

Q_{2}

-n túli meghosszabbítása

C

-n. Könnyen látható, hogy ez a két ponthármas ‐ az indexeket nem tekintve ‐ szimmetrikusan helyezkedik el

k

-nak

A

-ból induló átmérőjére nézve.
Megmutatjuk, hogy több megoldás nincs,

k

-nak bármely

P

-től és

Q

-tól különböző

R

pontjából indulunk is ki; a feladat szerinti három inverzió végrehajtása után mindig

R

-től különböző pontot kapunk. Ennek során

k

-nak a végpontjaival említett ívein mindig a két végpont által meghatározott rövidebb ívet értjük.
Ha

R

P P_{1}

íven van,

k_{1}

-re vonatkozó

R_{1}

inverze is ezen az íven van,

R_{2}

átkerül a

P P_{2}

ívre, és

R_{3}

is ezen az íven adódik, tehát nem lehet azonos

R

-rel.
Ha

R

P P_{2}

íven van,

R_{1}

P_{1} P_{2}

ívre kerül,

R_{2}

is itt keletkezik, és

R_{3}

P P_{1}

íven lesz, ismét nem lehet azonos

R

-rel.
Ha

R

P_{2} Q

íven van,

R_{1}

-et a

Q Q_{1}

ív mindenesetre tartalmazza,

R_{2}

pedig vagy

P_{1} Q_{2}

-re, vagy

P_{1} P_{2}

-re kerül,

R_{3}

eszerint vagy

Q Q_{2}

vagy

P P_{1}

-en lesz, és egyik esetben sem lehet

R

-rel azonos.
Végül ha

R

Q P_{1}

íven van,

R_{1}

P Q_{1}

ívre,

R_{2}

Q_{1} Q_{2}

ívre és

R_{3}

vagy

Q P_{2}

-re, vagy

P P_{2}

-re kerül. Egyik esetben sem kapunk tehát további megoldást.

Reviczky János (Budapest, I. István Gimn., II. o. t.)

Füredi Zoltán (Budapest, Móricz Zs. Gimn., II. o. t.)

Megjegyzés. Olyan

P

-t keresve, mely

P_{1}

-gyel és

P_{2}

-vel egy szabályos háromszög csúcsait adja, ez kimetszhető

k

-ból

A P C ∢ = 120^{\circ}

alapján az

A C

szakasznak azzal a

120^{\circ}

-os

i

látókörívével is, amely

A C

-nek

B

-t tartalmazó oldalán van.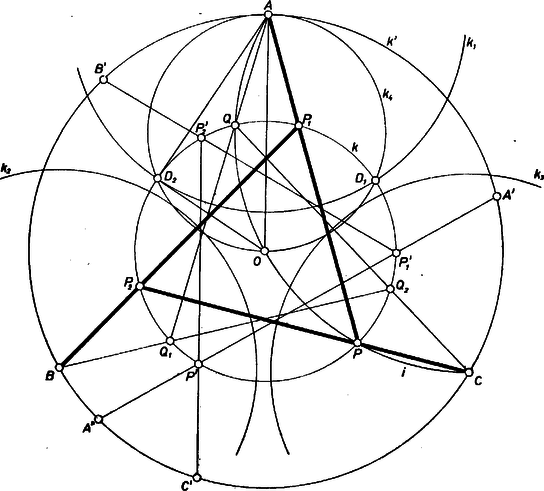

2. ábra