| Feladat: | Pontversenyen kívüli P.41 | Korcsoport: 14-15 | Nehézségi fok: nehéz |
| Megoldó(k): | Füredi Zoltán , Földvári Csongor , Gál P. , Göndőcs Ferenc , Katona Judit , Komócsi Sándor , Láz József , Lempert László , Less György , Papp Zoltán , Reviczky János , Szabó Lóránt , Szokoli I. , Várady T. | ||
| Füzet: | 1970/március, 119 - 120. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Számelrendezések, Számjegyekkel kapcsolatos feladatok, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1969/október: Pontversenyen kívüli P.41 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük -szel az egy egyenesen elhelyezett számok összegét a kívánt elrendezés esetén. Könnyű látni, hogy ekkor 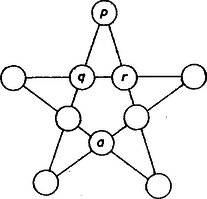 Válasszunk ki az ábrán két egyenest, s jelöljük a közös körükben levő számot -val, azt a számot pedig, amelyik egyik kiválasztott egyenesen sincs rajta, , , betűvel. Ekkor a két kiválasztott egyenesen álló számok összege ; ehhez hozzáadva a összeget, az összes különböző szám összegét, -öt kapjuk, ezért
Megmutatjuk, hogy a kívánt elrendezésben az és számok nem állhatnak sem két különböző egyenesen, sem ugyanazon az egyenesen; ebből következik, hogy válaszunk nemleges a feladat kérdésére. Az első esetben legyen a fentiekben kiválasztott két egyenes az a kettő, amelyik az számot tartalmazza. Ekkor (1)-ben és , , egyike, mondjuk , azaz , ami lehetetlen. A második esetben olyan egyenes van, mely és közül legalább az egyiket tartalmazza. Válasszuk ki most a két másik egyenest; ekkor , , között van is, is, például , . Behelyettesítve ezt (1)-be:
|