Kezdőlap


Feladat:	Pontversenyen kívüli P.40	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Füredi Zoltán , Göndőcs Ferenc , Komornik Vilmos , Simon Júlia , Vajnági András
Füzet:	1970/március, 117 - 119. oldal		PDF \| MathML
Témakör(ök):	Féligszabályos testek, Szabályos sokszögek által határolt testek, Térgeometriai számítások trigonometria nélkül, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/szeptember: Pontversenyen kívüli P.40

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vizsgáljuk meg, hány négyzet- és hány háromszöglap határolhat egy olyan poliédert, mely a feladat feltételeit kielégíti. Induljunk ki Euler tételéből, mely szerint ha $c$ -vel a csúcsok, $l$ -lel a lapok, $é$ -vel az élek számát jelöljük, akkor

\begin{matrix} c + l = é + 2. \end{matrix}

(1)

Legyen esetünkben a négyzetlapok száma

n

, a háromszögeké

h

.
Mivel a test minden csúcsa egy és csak egy négyzetlaphoz tartozik hozzá, másrészt pontosan négy háromszöglaphoz, azért

\begin{matrix} c = 4 n és c = \frac{3 h}{4}, \end{matrix}

innen

\begin{matrix} h = \frac{16}{3} n és l = n + h = \frac{19}{3} n . \end{matrix}

Továbbá minden csúcsban 5 él fut össze, és minden él 2 csúcsba fut be, így

5 c = 2 e

. Innen

\begin{matrix} e = \frac{5}{2} c = 10 n . \end{matrix}

Behelyettesítve (1)-be

c

l

és

e

talált kifejezéseit:

\begin{matrix} 4 n + \frac{19}{3} n = 10 n + 2. \end{matrix}

Ezt megoldva kapjuk, hogy ha a feladat feltételeit kielégítő poliéder létezik, akkor azt

n = 6

négyzetlap és

h = 32

háromszöglap határolja (továbbá azt is, hogy

24

csúcsa és

60

éle van). Kíséreljünk meg konstruálni ilyen testet!
A lapok szabályos volta miatt a poliéder összes élei egyenlők, négyzet-, valamint háromszög lapjai egybevágók. Egybevágók a csúcsoknál található testszögletek is. Azt sejtjük ezekből, hogy a poliéder alkalmas transzformáció útján önmagával fedésbe hozható, pl. négyzetlapjai átvihetők egymásba. Ezért feltesszük, hogy a 6 négyzetlap síkjai egy kockát határoznak meg. A konvexség alapján elég az olyan esetekre szorítkoznunk, amikor a poliéder négyzetlapjai a kocka oldallapjainak belsejébe esnek. Feltesszük továbbá, hogy a szemben levő oldallapok középpontjait összekötő egyenesek bármelyike (a kocka laptengelyei) körül

90^{\circ}

-kal, valamint a kocka csúcstengelyei (testátlói) körül

120^{\circ}

-kal elforgatva a poliéder a kockával együtt önmagába megy át. (Hangsúlyozzuk: nem bizonyítottuk, hogy csak ilyen típusú megoldás létezhet, csupán természetesnek tűnő feltételeket tettünk annak reményében, hogy van ezeket is kielégítő megoldás!) Nem jelenti az általánosság megszorítását, ha a kocka élét 2 egységnek választjuk, továbbá feltesszük, hogy ‐ az ábra jelölőseit használva ‐

P_{1}

A B C

háromszögben van.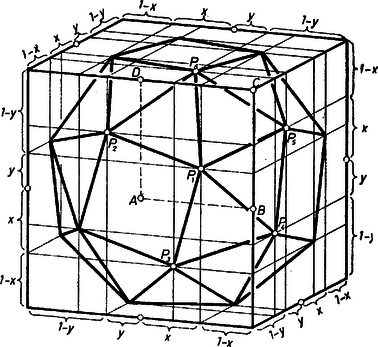

Jelöljük

P_{1}

nek az

A D

; ill. az

A B

egyenestől mért távolságát

x

-szel, ill.

y

-nal, ezekkel a

P_{1} P_{i} (i = 2, ... 6)

távolságokat könnyen kifejezhetjük, és ezek egyenlőségéből a feltett forgási szimmetriák alapján következik, hogy a poliéder összes élei egyenlők. Az ábrából kivehetően

\begin{matrix} P_{1} P_{2}^{2} & = P_{1} P_{3}^{2} = {(x - y)}^{2} + {(x + y)}^{2}, \\ P_{1} P_{4}^{2} & = {(2 y)}^{2} + {(1 - x)}^{2} + {(1 - x)}^{2}, \\ P_{1} P_{5}^{2} & = P_{1} P_{6}^{2} = {(1 - x)}^{2} + {(x - y)}^{2} + {(1 - y)}^{2} . \end{matrix}

Így a

\begin{matrix} P_{1} P_{2}^{2} = P_{1} P_{4}^{2}, P_{1} P_{2}^{2} = P_{1} P_{5}^{2} \end{matrix}

(2)

kétismeretlenes egyenletrendszert kell vizsgálnunk. Mivel azonban csak azt kell megállapítanunk, létezik-e a kívánt poliéder, nem szükséges megoldanunk az egyenletrendszert, csak megmutatni, hogy van a

0 < x < 1, 0 < y < 1

feltételeket kielégítő megoldása.
(2) azonos átalakítása útján:

\begin{matrix} y^{2} + 1 = 2 x, & (3) \\ x + & x y + y = 1, \end{matrix}

és

x

-et kiküszöbölve

\begin{matrix} y^{3} + y^{2} + 3 y - 1 = 0. \end{matrix}

Az egyenlet bal oldala

y = 0

-nál a

- 1

y = 1

-nél pedig a

+ 4

értéket veszi fel, és mivel folytonos függvénye

y

-nak, azért valamely közbülső

y_{0}

érték esetén

0

értékűvé válik. Ezen értéket (3)-ba helyettesítve a nyert

x_{0}

érték is

0

és

1

közé esik, hiszen

x = \frac{1}{2} (y_{0}^{2} + 1)

. Ez az

x_{0}

és

y_{0}

értékpár olyan

P_{1}

pontot határoz meg, mely kívánalmainknak megfelelő poliédert származtat (jóllehet lényegesen többet követeltünk meg, mint a feladat).

Füredi Zoltán, Göndőcs Ferenc, Vajnági András

Megjegyzés. A talált poliéder egyike az ún. Arkhimédész-féle félszabályos testeknek. (Ezeknek minden lapja szabályos sokszög ‐ éspedig legalább két különböző oldalszámú sokszög fordul elő rajtuk ‐, és minden csúcsukban ugyanannyi lap fut össze az előforduló szabályos sokszögek mindegyikéből.) Meg lehet mutatni, hogy az eredeti követelményeknek is csak egyetlen poliéder tesz eleget, továbbá annak síkra való tükörképe. (A poliédernek csak forgási szimmetriái vannak, tükrös szimmetriái nincsenek.) ‐ Egyébként a szabályos oktaéderből is leszármaztatható a poliéder. Annak a

8

háromszögnek a síkja határol szabályos oktaédert, amelynek mindegyik csúcsa a kockának másik-másik lapján van rajta, más szóval, amelyekhez mindegyik élük mentén háromszöglap kapcsolódik.