Kezdőlap


Feladat:	Pontversenyen kívüli P.39	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh János (Bp. I. István) , Fejes Gábor , Füredi Zoltán , Göndőcs Ferenc , Hermann Tamás , Kovács István (Bp. I. István) , Lempert László , Prőhle Tamás , Reviczky János , Simon Júlia , Simonyi Gyula , Tóth András (Bp. Könyves Kálmán) , Török István , Vajnági András , Váli László
Füzet:	1970/február, 74 - 77. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Körérintési szerkesztések, Alakzatok köré írt kör, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/szeptember: Pontversenyen kívüli P.39

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Érintse $k$ az $e$ és $f$ egyenest a $B$ , ill. $C$ pontban, és jelöljük $e$ és $f$ metszéspontját $A$ -val (1. ábr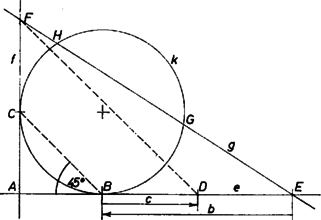a).

1. ábra

A körhöz külső pontból húzott szelőkre vonatkozó tétel szerint

\begin{matrix} b = E B = \sqrt[]{E G \cdot E H}, c = F C = \sqrt[]{F G \cdot F H} . \end{matrix}

(1)

Egyszerűség kedvéért a továbbiakban feltesszük, hogy

b > c

, és

E

F

G

H

különböző pontok.
Húzzunk

F

-en át

B C

-vel párhuzamost, messe ez

e

-t

D

-ben, így

B D = C F = c

E

-ből

D

-be az egymáshoz csatlakozó

E B

és

B D

szakaszokon keresztül juthatunk; ha ezek ellentétes irányúak, akkor

\begin{matrix} E D = b - c \end{matrix}

(

2 a

)

ha pedig megegyező irányúak, akkor

\begin{matrix} E D = b + c . \end{matrix}

(

2 b

)

Mivel a

D F

és

e

szöge

45^{\circ}

-os,

D

-ből az

E F

szakasz

45^{\circ}

-os vagy

135^{\circ}

-os szög alatt látszik, (2) alapján

D

-nek

E

-től mért távolsága is ismert, azért

D

megszerkeszthető.

D

meghatározza az

e

és

f

egyeneseket és ezekből

k

már könnyen meghatározható.

2. ábra

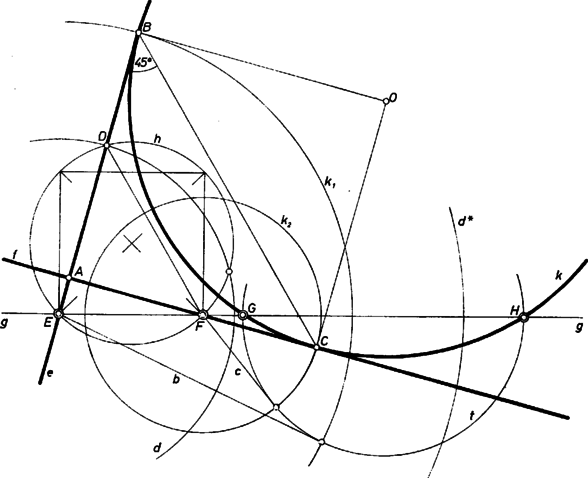Szerkesztésünk első lépéseként a

G H

szakasz fölé

t

Thalész-kört rajzolunk (2. ábra). Az

E

F

pontból egy-egy érintőt húzunk

t

-hez, ezek hossza

b

, illetve

c

. Az

E

pont körül

b - c

és

b + c

, sugárral kört rajzolunk, ez

d

, ill.

d^{*}

. Majd az

E F

szakasz fölé

g

egyik oldalán négyzetet szerkesztünk, az e köré írt kör legyen

h

. A

h

és

d

(vagy

h

és

d^{*}

) körök egyik metszéspontja legyen

D

, ekkor

E D

a keresett

e

egyenes, erre

F

-en át merőlegest rajzolva kapjuk

f

-et,

e

és

f

metszéspontja

A

. Az

e

egyenesen

E

-ből

D

felé felmérjük az

E B = b

szakaszt, a kapott

B

ponton át párhuzamost húzunk

D F

-fel, ez

f

-et

C

-ben metszi. Végül

A

-t tükrözzük a

B C

egyenesre, kapjuk

O

-t, a keresett

k

kör az

O

körül rajzolt,

O B

sugarú kör lesz.
A szerkeszthetőség első feltétele, hogy az

E

F

pontok ne legyenek rajta a

G H

szakaszon. Ez kétféleképpen teljesülhet: az

E F

szakasz vagy tartalmazza a

G H

szakaszt, vagy nincs vele közös pontja. Ha ez teljesült, akkor a leírt szerkesztés a

d

d^{*}

h

körök megrajzolásáig elvégezhető. Megjegyezzük, hogy a

h

kört a

g

egyenes bármelyik oldalán felvehetjük, hiszen feladatunk tetszőleges megoldását

g

-re tükrözve ismét megoldást kapunk.
A

h

kör átmérője

\begin{matrix} h = \sqrt[]{2} E F, \end{matrix}

(3)

így

d

és

h

csak akkor metszik egymást, ha

\begin{matrix} h ≧ b - c, \end{matrix}

(

4 a

)

és egyenlőség esetén

1

, különben

2

metszéspontjuk van.
A

d^{*}

és

h

körök esetében hasonlóan

\begin{matrix} h ≧ b + c \end{matrix}

(

4 b

)

D

metszéspont létrejövésének a feltétele. Könnyen látható, hogy a

D

pont meghatározása után fenti szerkesztésünk egyértelműen végrehajtható.
A továbbiakban, ha az

E F

szakasz tartalmazza a

G H

szakaszt, akkor

\begin{matrix} b = \sqrt[]{E G \cdot E H} < \frac{1}{2} (E G + E H), \\ c = \sqrt[]{F G \cdot F H} < \frac{1}{2} (F G + F H) \end{matrix}

miatt

b + c < E F

, tehát

(4 a)

-ban is,

(4 b)

-ben is az egyenlőtlenség teljesül, a

g

-re való tükrözést is figyelembe véve

8

megoldást kapunk. Ha viszont az

E F

G H

szakaszoknak nincs közös pontjuk, az is előfordulhat, hogy

(4 a)

sem teljesül, és a feladatnak nincs megoldása.
Rátérünk szerkesztésünk helyességének bizonyítására. A körhöz külső pontból húzott szelők darabjaira vonatkozó tétel szerint bármely, a

G

H

pontokon átmenő körhöz húzunk is érintőt az

E

F

pontokból, ezek hossza az (1) alatti

b

és

c

, jogosan neveztük tehát az általunk megszerkesztett szakaszokat

b

-nek és

c

-nek. A szerkesztés további menetéből közvetlenül következik, hogy a kapott

e

f

egyenesek merőlegesek egymásra; rendre átmennek az

E

F

pontokon; az

A D F

háromszög egyenlő szárú és derékszögű, és

E B = b

.
Ha a

D

pont a

h

és

d

körök metszéspontja,

E D = b - c < E B

D

tehát az

E B

szakaszon , és

D B = F C = c

. Ha viszont

D

h

és

d^{*}

metszéspontja,

E D = b + c > E B

, ekkor

B

van az

E D

szakaszon, de ismét

D B = F C = c

. Mivel az

A B C

háromszög is egyenlő szárú és derékszögű,

A B O C

négyzet, és

k

B

C

pontokban érinti az

e

f

egyeneseket. Mivel

k

-hoz az

E

F

pontokból húzott érintők hossza rendre

b

, illetve

c

k

merőlegesen metszi az

E

középpontú,

b

sugarú

k_{1}

kört és az

F

középpontú,

c

sugarú

k_{2}

kört. Megmutatjuk, hogy a

k_{1}

k_{2}

köröket merőlegesen metsző körök mindegyike átmegy a

G

H

pontokon.
Azt már beláttuk, hogy tetszőleges, a

G

és

H

pontokon átmenő kör merőlegesen metszi a

k_{1}

k_{2}

köröket. Legyen

P

(a síkon) tetszőleges, de nem a

g

egyenesen levő pont. Ha

k_{0}

P

-n is átmenő, a

k_{1}

k_{2}

, köröket merőlegesen metsző kör, az

E P

F P

félegyenesek

k_{0}

-t olyan

P_{1}

P_{2}

pontokban metszik, amelyekre

\begin{matrix} E P \cdot E P_{1} = b^{2}; F P \cdot F P_{2} = c^{2}, \end{matrix}

ami a

P_{1}

P_{2}

pontokat egyértelműen meghatározza.
Könnyen látható, hogy a

k_{1}

k_{2}

körök nem metszhetik egymást, így a

P_{1}

P_{2}

pontok közül legalább az egyik

P

-től különböző. Ha tehát

k_{0}

átmegy

P

-n, és a

k_{1}

k_{2}

köröket merőlegesen metszi, át kell mennie a sík egy további ‐

P

k_{1}

és

k_{2}

által egyértelműen meghatározott ‐

Q

pontján is. Továbbmenve

Q

-ból

k_{0}

-nak egy további ‐ ugyancsak egyértelműen meghatározott ‐

R

pontjához jutunk, a sík tetszőleges (nem a

g

egyenesen levő)

P

pontján át tehát legfeljebb egy kör mehet át, mely a

k_{1}

k_{2}

körüket merőlegesen metszi. A

P G H

háromszög köré írható kör merőlegesen metszi őket, így mindegyik, a

k_{1}

k_{2}

köröket merőlegesen metsző kör átmegy a

G

H

pontokon. Ezzel bizonyításunkat befejeztük. ‐ A diszkussziót ‐ hely hiányában ‐ az olvasóra hagyjuk.

Megjegyzések. 1. A figyelmen kívül hagyott

b = c

esetben egyszerű Apollóniosz-feladattal állunk szemben.
2. Hasonlóan oldható meg a feladat akkor is, ha

e

és

f

között tetszőleges szöget írunk elő.