Kezdőlap


Feladat:	Pontversenyen kívüli P.35	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Balogh Zoltán , Beck József , Göndőcs Ferenc , Hanák László , Horváth Miklós , Iván László , Kirchner Imre , Komornik Vilmos , Pál Jenő , Reviczky János
Füzet:	1970/február, 67 - 71. oldal		PDF \| MathML
Témakör(ök):	Nevezetes azonosságok, Másodfokú diofantikus egyenletek, Magasabb fokú diofantikus egyenletek, Oszthatósági feladatok, "a" alapú számrendszer (a >1, egész szám), Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/május: Pontversenyen kívüli P.35

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat nem kívánta az összes, a feltételeket kielégítő szám megadását. Különböző ésszerű megszorítás mellett már kevés próbálgatással lehetett megoldást találni. Az alábbiakban eljárást mutatunk az összes megoldás megkeresésére.

Megoldás. Jelöljük a keresett szám jegyeit

x

y

-nal, azaz a számot

100 x + y

alakban írjuk, ahol

x \neq 0

, mivel a szám kétjegyű, s így

\begin{matrix} 0 < x ≦ 99, 0 ≦ y ≦ 99. \end{matrix}

(1)

A feladat a következő egyenlet teljesülését kívánja:

\begin{matrix} (100 x + y) (x + y) = x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2}) . \end{matrix}

(2)

Mivel feltételeink szerint

x + y > 0

, így ez az egyenlet ekvivalens az

x + y

szorzó elhagyásával keletkező egyenlettel, amit

y

hatványai szerint rendezünk,

4

-gyel megszorzunk és teljes négyzetté kiegészítünk.

\begin{matrix} 4 y^{2} - 4 (x + 1) y - 4 x (100 - x) = {(2 y - x - 1)}^{2} - [{(x + 1)}^{2} + 4 x (100 - x)] = 0. \end{matrix}

Jelöljük

2 y - x - 1

-et

z

-vel. Ennek abszolút értéke nagyobb, mint

x + 1

, mert pozitív

x

-re a szögletes zárójel mindkét tagja pozitív. Ez azonban (1) mellett csak úgy lehet, ha

2 y > x + 1

, azaz

z

pozitív. Másrészt (1) mellett a szögletes zárójel első tagja legalább

4

, a második legalább

396

, mert

x = 1

-re ennyi, ha pedig

x > 1

, akkor (1) mellett

x

és

100 - x

közül a kisebbik is legalább

2

, a nagyobb legalább

50

. Így

z ≧ 20

.
Bontsuk tagokra és alakítsuk teljes négyzetté a fent a szögletes zárójelben levő kifejezést is:

\begin{matrix} {(2 y - x - 1)}^{2} + 3 {(x - 67)}^{2} = 13 468, \end{matrix}

vagy

\begin{matrix} x - 67 = t \end{matrix}

(3)

jelöléssel:

\begin{matrix} z^{2} + 3 t^{2} = 13 468. \end{matrix}

(4)

Az eredeti ismeretleneket az újakkal kifejezve:

\begin{matrix} x = t + 67, y = \frac{z + t}{2} + 34. \end{matrix}

(

3'

)

A (

3'

), (4) együttesen ekvivalens (2)-vel, sőt (

3'

) a (2) és (4) egész számokból álló megoldásait is kölcsönösen egymáshoz rendeli, hiszen világos, hogy ha

x

y

egész, akkor

z

és

t

is. Fordítva pedig azért teljesül állításunk, mert (4) egész megoldásaiban vagy

z

is,

t

is páros, vagy mind a kettő páratlan, így (

3'

) szerint

x

mellett

y

is egész.
A (4) egyenletnek csak véges sok egész megoldása lehet, hiszen a bal oldal mindegyik tagja legfeljebb a jobb oldallal lehet egyenlő, így ‐ a

z

-re már talált alsó korlátot is tekintetbe véve ‐

\begin{matrix} 20 ≦ z ≦ 116 | t | ≦ 67. \end{matrix}

(5)

A korlátok meghatározása közben az is kiderül, hogy mindegyik elő is fordul a megoldások közt. Az első

x = 1

-re adódott, ekkor

z = 20

y = 11

t = - 66

t = 66

-ra

x

már túl nagynak adódik. Egyáltalán (1) és (3) alapján

\begin{matrix} t ≦ 32. \end{matrix}

(

5'

)

(4) további, az (5), (

5'

)-t kielégítő megoldásai

z = 116

t = \pm 2

. (A

z = 1

t = - 67

megoldás nem valódi, mert az egyjegyű számra vezető

x = 0

y = l

értékpárt adja.)Innen

x = 69

y = 93

és

x = 65

y = 91

adódik. Ezzel

3

megoldást már találtunk, a feladat kívánalmainak tehát eleget tettünk; megkeressük azonban a további megoldásokat is.
A próbálgatások számának csökkentésére felhasználható

13 468

oszthatósága

7

-tel és

13

-mal, ugyanis így

\begin{matrix} z^{2} + 3 t^{2} - 7 t^{2} = (z + 2 t) (z - 2 t) \end{matrix}

is osztható kell hogy legyen

7

-tel. Hasonlóan

\begin{matrix} z^{2} + 3 t^{2} - 13 z^{2} = 3 (t + 2 z) (t - 2 z) \end{matrix}

osztható

13

-mal. Mivel

t

-vel együtt

- t

is megoldása (4)-nek, választhatjuk

t

előjelét úgy, hogy

z + 2 t

legyen

7

-tel osztható:

\begin{matrix} z + 2 t = 7 c, \end{matrix}

(6)

ahol

c

alkalmas egész. Továbbá mivel

13

prím és nem osztója

3

-nak, kell hogy

\begin{matrix} t + 2 z = 13 d_{1} vagy t - 2 z = 13 d_{2} \end{matrix}

(7)

teljesüljön alkalmas egész

d_{1}

-gyel, ill.

d_{2}

-vel.
Ha a (7) alatti első egyenlőség teljesül, akkor ennek

7

-szereséből levonva (6)-nak

13

-szorosát:

\begin{matrix} z - 19 t = 91 (d_{1} - c) . \end{matrix}

Mivel

z

és

t

egyszerre páros, ill. páratlan, így magyar

d_{1} - c

páros. Értékét

2 m

-mel jelölve

\begin{matrix} z = 19 t + 182 m . \end{matrix}

(8)

Ezt (4)-be helyettesítve

364

-gyel egyszerűsíthetünk, és a következő egyenletre jutunk:

\begin{matrix} t^{2} + 19 m t + 91 m^{2} - 37 = 0. \end{matrix}

(9)

Ha pedig a (7) alatti második egyenlőség teljesül, akkor ennek

7

-szereséhez hozzáadva (6)-nak

13

-szorosát:

\begin{matrix} 33 t - z = 91 (d_{2} + c) . \end{matrix}

Itt

d_{2} + c = 2 n

páros szám kell hogy legyen. Így

\begin{matrix} z = 33 t - 182 n, \end{matrix}

(10)

és (4) a következő egyenletbe megy át,

364

-gyel való egyszerűsítés után:

\begin{matrix} 3 t^{2} - 33 n t + 91 n^{2} - 37 = 0. \end{matrix}

(11)

A (9) egyenlet megoldása

\begin{matrix} t = \frac{- 19 m \pm \sqrt[]{148 - 3 m^{2}}}{2} = \frac{- 19 m \pm D_{1}}{2}, \end{matrix}

a (11) egyenleté

\begin{matrix} t = \frac{33 n \pm \sqrt[]{444 - 3 n^{2}}}{6} = \frac{33 n \pm D_{2}}{6} . \end{matrix}

Az első csak

| m | ≦ \sqrt[]{148 / 3} < 8

esetén ad valós megoldást, az utóbbi

| n | ≦ \sqrt[]{444 / 3} < 13

esetben. Ez néhány próbálgatást igényel összesen. Csak

| m | = 3

4

7

, ill.

| n | = 1

10

11

jön tekintetbe. A fenti

t

értékekhez tartozó

z

értékek (8), ill. (10) alapján

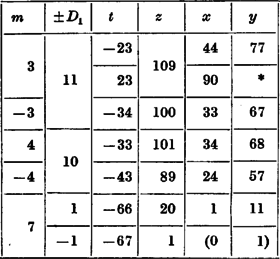
\begin{matrix} z = \frac{3 m \pm 19 D_{1}}{2}, ill . z = \frac{- n \pm 11 D_{2}}{2} . \end{matrix}

A (6) egyenlőségnél minden

z

értékhez

t

-nek csak azt az előjelválasztását vettük tekintetbe, amelyikre az ebben az egyenlőségben szereplő tényező osztható

7

-tel. Hogy az összes megoldást megkapjuk, emellett

- t

-t is tekintetbe kell vennünk. Az így adódó és (5), (

5'

)-t kielégítő megoldásokat az alábbi táblázatok adják. A

^{*}

azt jelöli, hogy az illető ismeretlenre nem megfelelő érték adódik; az ilyen rovatokat természetesen nem folytattuk.
A (8)-ból adódó megoldások:

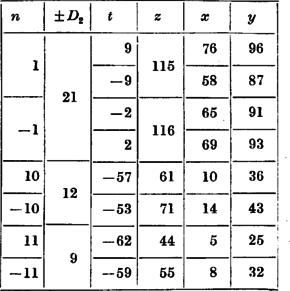
A (10)-ből adódó megoldások:

A feladat követelményeinek megfelelő összes számok (tízes számrendszerben felírva)

\begin{matrix} 111, 525, 832, 1036, 1443, 2457, 3367,3468, 4477, 5887, 6591, 6993, 7696 \end{matrix}

Balogh Zoltán (Debrecen, Fazekas Mihály Gimn., I. o. t.)

Megjegyzések. 1. A (2)-nek

x + y

-nal való osztása útján adódó egyenlet így is alakítható:

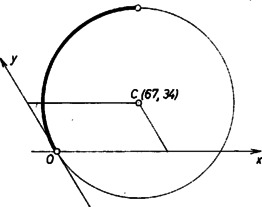
\begin{matrix} {(x - 67)}^{2} + {(y - 34)}^{2} - (x - 67) (y - 34) = 3367. \end{matrix}

Ez kör egyenlete abban a (ferdeszögű) koordináta-rendszerben, melynek pozitív féltengelyei

120^{\circ}

szöget zárnak be egymással (egyébként egy

P

pont

x

y

koordinátája az az irányított szakasz, melynek kezdőpontja a

P

-n át az

x

y

tengellyel párhuzamosan húzott egyenesnek az

y

, ill.

x

tengellyel való metszéspontja, végpontja pedig

P

). Éspedig a kör középpontja a

(67,34)

pont, és egy kerületi pontja az origó (hiszen az eredeti alakot kielégíti

x = y = 0

; a

(0,1)

pont is rajta van a körön. Minden egyes talált megoldásunknak egy rácspont felel meg a körnek az (1)-et kielégítő ívén. ‐ Ezek alapján a talált különböző megoldások között kapcsolatok fedezhetők fel.

2. A problémát tízes számrendszerben értve az 1967. évi Arany Dániel tanulóverseny egyik feladata adódik (II. forduló 1. feladata a haladók korcsoportjában, az általános tantervű osztályok részére; lásd K. M. L. 35 (1967) 6. o.).