Kezdőlap


Feladat:	Pontversenyen kívüli P.32	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beck József
Füzet:	1970/február, 62 - 66. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek egybevágósága, Háromszögek hasonlósága, Középpontos tükrözés, Numerikus és grafikus módszerek, Terület, felszín, ( x + 1/x ) > = 2 ( x > 0 ), Paralelogrammák, Síkgeometriai számítások trigonometria nélkül négyszögekben, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/április: Pontversenyen kívüli P.32

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tükrözzük az $A B C D$ négyszöget a $B'$ pontra, kapjuk az $E F G H$ négyszöget (1. ábra), ahol 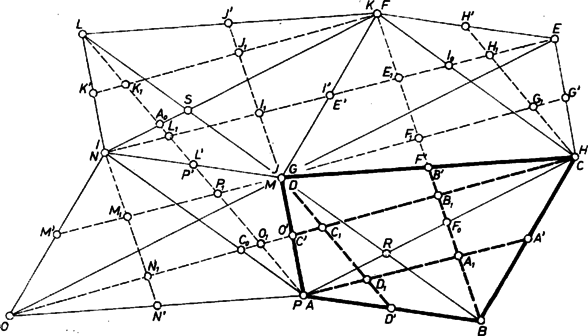$G$ azonos $D$ -vel, $H$ azonos $C$ -vel.

1. ábra

Állítsuk elő az új négyszögben az

E'

F'

G'

H'

és

E_{1}

F_{1}

G_{1}

H_{1}

pontokat ugyanúgy, mint az eredeti négyszög megfelelő pontjait. Az új négyszöget

E'

-re tükrözve kapjuk az

I J K L

négyszöget (

J

D_{2}

-vel,

K

F

-fel azonos), és ebben hasonlóan állítsuk elő a további 4‐4 pontot, végül ezt a négyszöget

L'

-re tükrözve az

M N O P

négyszöget kapjuk (

M

D

-vel,

N

J

-vel azonos).
Mivel

D

-ben az eredeti négyszögnek mind a négy szöge fellép, az

M P

egyenes azonos

D A

-val, a tükrözések miatt

A D = E H = I L = M P

, tehát

P

és

A

is azonos, és utolsó négyszögünk az eredetiből

C'

-re való tükrözéssel is előállítható.
A

B_{1} E_{1} L_{1} O_{1}

négyszög

T_{2}

területe egyenlő

(T - T_{1})

-gyel, hiszen e négyszögnek az előbbi négy négyszögbe eső darabjai rendre egybevágóak az eredeti

A B C D

négyszög

T_{1}

-en kívüli részének rendre egy-egy darabjával. Az

A C F I

négyszög oldalai rendre párhuzamosak az eredeti négyszög megfelelő átlóival, ez tehát paralelogramma, és területe az eredeti négyszög területének kétszerese:

P = 2 T

Jelöljük a

B_{1} E_{1}

E_{1} L_{1}

L_{1} O_{1}

O_{1} B_{1}

egyenesnek az

A C

C F

F I

I A

oldalon levő pontját rendre

F_{0}

I_{0}

A_{0}

C_{0}

-lal, az

A C

B D

átlók metszéspontját

R

-rel, és legyen

\begin{matrix} p = \frac{A R}{A C}; q = \frac{R C}{A C}; r = \frac{D R}{D B}; s = \frac{R B}{D B}; \end{matrix}

(1)

\begin{matrix} α = \frac{I A_{0}}{I F}; β = \frac{A C_{0}}{A I}; γ = \frac{C F_{0}}{C A}; δ = \frac{F I_{0}}{F C} \end{matrix}

(2)

Ekkor

p + q = 1

r + s = 1

. Legyen még

I F

és

D L

metszéspontja

S

. Az

A_{0} S L

A R L

háromszögek hasonlóak, emiatt

\begin{matrix} A_{0} S : S L = A R : R L, \\ S L \cdot A R = A_{0} S \cdot R L \\ \frac{S L}{B D} \cdot \frac{A R}{A C} = \frac{A_{0} S}{A C} \cdot \frac{R L}{B D}, \end{matrix}

\begin{matrix} r \cdot p = (p - α) (1 + r), \\ α = \frac{p}{1 + r} . \end{matrix}

Hasonló módon kapjuk, hogy

\begin{matrix} β = \frac{r}{1 + q}, γ = \frac{q}{1 + s}, δ = \frac{s}{1 + p} . \end{matrix}

(3)

2. ábra

L_{1}

-en át

A C

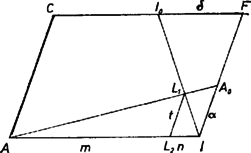-vel párhuzamosan húzott egyenes messe

A I

-t

L_{2}

-ben, és legyen (2. ábra)

\begin{matrix} \frac{L_{1} L_{2}}{A C} = t; \frac{A L_{2}}{A I} = m; \frac{L_{2} I}{A I} = n . \end{matrix}

A L_{1} L_{2}

és

A A_{0} I

hasonló háromszögek alapján

t = m α

, hasonló módon kapjuk, hogy

t = \frac{n}{δ}

, ezek alapján

\begin{matrix} t = \frac{α}{1 + δ α} . \end{matrix}

A C F I

és

A L_{1} I

idomok területének aránya tehát:

\begin{matrix} \frac{T_{A L I_{1}}}{P} = \frac{1}{2} \cdot \frac{α}{1 + δ α} . \end{matrix}

Hasonló módon kapjuk, hogy

\begin{matrix} \frac{T_{C O_{1} A}}{P} = \frac{1}{2} \cdot \frac{β}{1 + α β}, \frac{T_{F B_{1} C}}{P} = \frac{1}{2} \cdot \frac{γ}{1 + β γ}, \frac{T_{I E_{1} F}}{P} = \frac{1}{2} \cdot \frac{δ}{1 + γ δ} . \end{matrix}

Jelöljük e négy háromszög területének összegét

Q

-val akkor

\begin{matrix} \frac{2 Q}{P} = \frac{α}{1 + δ α} + \frac{β}{1 + α β} + \frac{γ}{1 + β γ} + \frac{δ}{1 + γ δ} . \end{matrix}

(4)

Fenti összefüggéseink alapján

P = 2 T

Q = P - T_{2} = P - T + T_{1} = T + T_{1}

így

\begin{matrix} \frac{2 Q}{P} = \frac{2 T + 2 T_{1}}{2 T} = 1 + \frac{T_{1}}{T} . \end{matrix}

Azt kell tehát megmutatnunk, hogy

\begin{matrix} 1 + \frac{1}{6} ≦ \frac{2 Q}{P} ≦ 1 + \frac{1}{5} . \end{matrix}

(5)

(3) és (4) alapján

\begin{matrix} \frac{2 Q}{P} = \frac{p (p + 1)}{s p + (p + 1) (r + 1)} + \frac{r (r + 1)}{p r + (r + 1) (q + 1)} + \frac{q (q + 1)}{r q + (q + 1) (s + 1)} + \frac{s (s + 1)}{q s + (s + 1) (p + 1)} . \end{matrix}

Avégett, hogy ezt a kifejezést könnyebben tudjuk kezelni, vezessük be új változóknak az egyes nevezőkben álló kifejezéseket. Mivel

p + q = r + s = 1

, ezek értéke:

\begin{matrix} 1 + 2 p + r = 5 x, \\ 1 + 2 r + q = 5 y, & (6) \\ 1 + 2 q + s = 5 u, \\ 1 + 2 s + p = 5 v . \end{matrix}

Új változóinkkal a régieket kifejezve kapjuk, hogy

\begin{matrix} p + 1 = 2 x + v, p = 2 x - y, \\ r + 1 = 2 y + x, r = 2 y - u, & (7) \\ q + 1 = 2 u + y, q = 2 u - v, \\ s + 1 = 2 v + u, s = 2 v - x . \end{matrix}

Ezek alapján

\begin{matrix} \frac{2 Q}{P} = \frac{(2 x + v) (2 x - y)}{5 x} + \frac{(2 y + x) (2 y - u)}{5 y} + \frac{(2 u + y) (2 u - v)}{5 u} + \frac{(2 v + u) (2 u - x)}{5 v} = \\ = \frac{4}{5} (x + y + u + v) - \frac{1}{5} (\frac{v y}{x} + \frac{x u}{y} + \frac{y v}{u} + \frac{u x}{v}) = \frac{8}{5} - \frac{1}{5} (\frac{v y}{x u} + \frac{x u}{v y}) . \end{matrix}

Közben többször használtuk, hogy

x + u = y + v = 1

, ami (6)-ból közvetlenül látható. (5) alapján azt kell belátnunk, hogy

\begin{matrix} 2 ≦ \frac{v y}{x u} + \frac{x u}{v y} ≦ \frac{16}{3} . \end{matrix}

(8)

A bal oldal könnyen belátható, hiszen

x

y

u

v

pozitívak, így pozitív a

\frac{v y}{x u}

szám is, és egy pozitív számnak és reciprokának az összege valóban legalább

2

. Egyenlőség akkor és csak akkor teljesül, ha a mondott hányados

1

-gyel egyenlő; ez a helyzet pl. ha az eredeti négyszög négyzet. A jobb oldali egyenlőtlenség pedig abból fog következni, hogy megmutatjuk,

\frac{v y}{x u}

szám

\frac{2}{3}

és

\frac{3}{2}

között van.

\frac{3}{2}

-hez tetszőleges közeli értéket kapunk pl., ha a négyszög egyik oldala elég kicsi a többihez képest.
Mivel

0 ≦ p ≦ 1

0 ≦ r ≦ 1

, (7) alapján kapjuk, hogy az

x,

y

értéke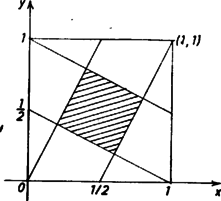k a

\begin{matrix} 0 ≦ 2 x - y ≦ 1, \\ 0 ≦ 2 y - x - 1 ≦ 1 & (9) \end{matrix}

egyenlőtlenségekkel meghatározott tartományban vannak, melyet az

x

y

síkon a 3. ábra mutat be.

3. ábra

Azt kell tehát megmutatnunk, hogy ezen a tartományon

\begin{matrix} \frac{2}{3} ≦ \frac{y (1 - y)}{x (1 - x)} ≦ \frac{3}{2} . \end{matrix}

Mivel

x

és

y

szerepét felcserélve a kifejezés értéke saját reciprokába megy át, és a vizsgált tartomány egy hasonló típusú tartományba, elegendő például a jobb oldalt bebizonyítanunk. Rögzített

x

értékek mellett a kifejezés értéke annál nagyobb, minél messzebb van

y

értéke

1 / 2

-tő1, a kifejezés legnagyobb értékét tehát a tartomány határán kapjuk. Például az

y = 2 x

egyenesen a kifejezés értéke

\begin{matrix} \frac{2 x (1 - 2 x)}{x (1 - x)} = 4 - \frac{2}{1 - x}, \end{matrix}

ami

x

-ben monoton változik. így szélső értékeit a vizsgált szakasz végpontjaiban veszi fel:

x = \frac{1}{5}

, illetve

x = \frac{2}{5}

mellett, ekkora kifejezés értélre

\frac{3}{2}

, illetve

\frac{2}{3}

Hasonló módon kapjuk, hogy a kifejezés értéke a többi oldalszakaszon is monoton változik, és a másik két csúcsban is

\frac{3}{2}

, illetve

\frac{2}{3}

az értéke, állításunkat ezzel bizonyítottuk.