| Feladat: | Pontversenyen kívüli P.31 | Korcsoport: - | Nehézségi fok: nehéz |
| Megoldó(k): | Beck József , Göndőcs Ferenc , Somorjai Gábor , Vajnági András | ||
| Füzet: | 1969/november, 155 - 156. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Inverzió, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1969/április: Pontversenyen kívüli P.31 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Feltehetjük, hogy és különböző pontok, hiszen ha azonosak, az állítás nyilvánvaló. Legyen a , pontokon átmenő, tetszőleges kör, és jelöljük -vel alkotott metszéspontjait -rel, -vel. (Mivel elválasztja a , pontokat, és mindig létrejön.) Az kört -re invertálva és pontja felcserélődik, az , pontok helyükön maradnak, így is önmagába megy át. Az , egyeneseken -nek csak egy-egy pontja lehet ( a kör középpontja), így ezek az egyenesek érintik -t, és tehát merőlegesen metszik egymást. 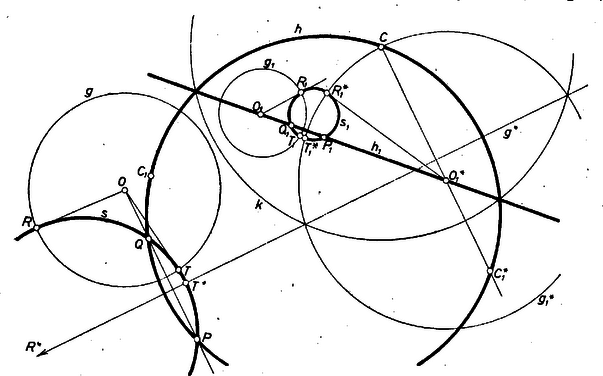 Hasonló állítás igaz, ha egyenes (a továbbiakban a megfelelő egyenest ‐ az egyértelműség kedvéért ‐ -gal jelöltük), hiszen ha átmegy a -ra szimmetrikus , pontokon, akkor középpontja -on van, vagyis és merőlegesek. A , pontokon átmenő tetszőleges kör tehát merőleges -re. (Ezek közé a körök közé sorolhatjuk a egyenest is, ez nyilvánvalóan merőleges -re.) Vigye át a középpontú körre vonatkozó inverzió -et -be, az , pontokat , -be. Mivel az inverzió szögtartó, is merőleges lesz -re, így , érintik -et ( a középpontja). (Hasonló állítás igaz a egyeneshez tartozó , metszéspontok , inverzére is: a kör is merőlegesen metszi -et, tehát , is érinti -et, ahol a kör középpontját jelöli.) Az kört -re invertálva, önmagába megy át, hiszen , pontjai helyükön maradnak, és az inverz képnek is merőlegesen kell metszenie -et. Állításunk tetszőleges, a , pontokon átmenő körre igaz, hiszen ha egy tetszőlegesen felvett körből indulunk ki, és ezt invertáljuk -ra, a kapott kör ‐ vagy egyenes ‐ átmegy a , pontokon. Ezek szerint a , pontokon átmenő köröket -re invertálva, azok mindegyike önmagába megy át. Ez az inverzió a körök egyik közös pontját, a -et csak olyan pontba viheti, amelyik mindegyik körön rajta van, tehát képe , amint azt bizonyítani akartuk. ( képe nem lehet önmaga, hiszen nincs rajta -en, mint ahogy sincs rajta -n.) Bizonyításunknak ez az utolsó része változtatás nélkül mondható el a körre is, feladatunk állítását tehát bebizonyítottuk. II. Legyen a , , pontok által meghatározott kör vagy egyenes (tehát a egyenes, ha rajta van -n, és a , , pontokon átmenő kör, ha ezek nincsenek egy egyenesen). Mint a , pontokon átmenő körök mindegyike, is merőlegesen metszi -t (és -ot is). Emiatt -nak -ra vonatkozó inverze is merőlegesen metszi -et (és -ot is). Az (és ) pont tehát rajta van -en. Másrészt -t -re invertálva (illetve -ra tükrözve) önmagába megy át, a pont -re vonatkozó inverze (illetve -ra vonatkozó tükörképe) szintén rajta van -n, és a -ra vonatkozó invertálás épp ezeket viszi az , pontokba, tehát a P.12. feladat állítását is bebizonyítottuk.
|