Kezdőlap


Feladat:	Pontversenyen kívüli P.29	Korcsoport: -	Nehézségi fok: nehéz
Megoldó(k):	Beck József , Göndőcs Ferenc
Füzet:	1969/november, 152 - 154. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat, Konstruktív megoldási módszer, Teljes indukció módszere, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/április: Pontversenyen kívüli P.29

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

\begin{matrix} f_{1} (x) = f (x) = a x^{2} + b x + c \end{matrix}

másodfokú függvényből kiindulva az

\begin{matrix} f_{i + 1} (x) = f (f_{i} (x)) (i = 1,2, ...) \end{matrix}

(2)

rekurzióval egy függvénysorozatot képezünk. Ha az

\begin{matrix} x_{1}, x_{2}, ..., x_{n + 1} \end{matrix}

számok eleget tesznek (1)-nek, akkor

\begin{matrix} x_{i + 1} = f_{i} (x_{1}), (i = 1, 2, ..., n) \end{matrix}

(3)

és így

x_{1}

gyöke az

\begin{matrix} f_{n} (x) = x \end{matrix}

(4)

egyenletnek. Megfordítva: a (4) egyenlet tetszőleges gyökét véve

x_{1}

nek, az

x_{2}

...

x_{n + 1}

számokat pedig (3) alapján definiálva, az (1) rendszer egy megoldásrendszerét kapjuk.
Könnyíti az áttekintést, ha az

f (x)

függvényt olyan szakaszon vizsgáljuk, ahol értékkészlete és értelmezési tartománya azonos: ez a közös halmaz lesz a (2) rekurzióval definiált függvények értelmezési tartománya is. Emiatt választjuk az

\begin{matrix} f (x) = f_{1} (x) = 2 x^{2} - 1 \end{matrix}

(5)

függvényt, mely a

(- 1,1)

zárt intervallumot önmagára képezi le. Megmutatjuk, hogy (5)-ből kiindulva és (2) szerint állítva elő az

f_{n} (x)

függvényt, a kapott (4) egyenletnek legalább három gyöke van, tehát

a = 2

b = 0

c = - 1

megfelelő együtthatók.
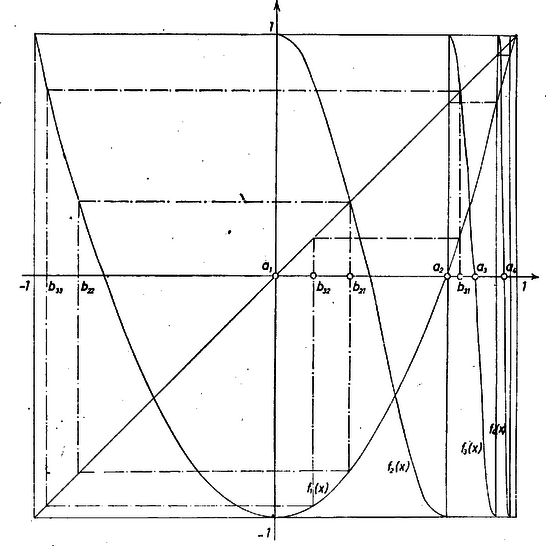
A (4) egyenlet nyilvánvaló gyöke az

\begin{matrix} f (x) = x \end{matrix}

egyenlet két gyöke, az

A = - 1 / 2

, és a

B = 1

szám, így egyetlen további gyök létezését kell kimutatnunk.

Az (5) függvény a

(0,1)

zárt szakaszon monoton nő

- 1

-től

+ 1

-ig, így egyértelműen meghatározott a

[- 1,1]

számközben az a

φ

függvény, amely az

x

számhoz azt a számot adja meg, amelyre

f

értéke

x

(ezt a függvényt nevezzük

f

inverzének). A

φ

függvény a

[- 1,1]

zárt szakaszbeli számokhoz a

[0,1]

zárt szakasz számait rendeli hozzá, az előbbi szakaszt az utóbbira képezi le. Az

a_{1} = 0

értékből kiindulva képezzük az

\begin{matrix} a_{i + 1} = φ (a_{i}) (i = 1, 2, ...) \end{matrix}

(6)

rekurzióval az

a_{i}

sorozatot. Mivel a

φ (x)

függvény is monoton nő, és értékkészlete a

(0,1)

zárt intervallum,

\begin{matrix} 0 = a_{1} < a_{2} < ... < a_{i} < ... ≦ 1. \end{matrix}

(7)

φ

függvény a

(- 1, 0)

szakaszt az

(a_{1}, a_{2})

szakaszra, ezt a szakaszt az

(a_{2}, a_{3})

szakaszra képezi le, és általában az

(a_{i}, a_{i + 1})

intervallumot a szomszédos

(a_{i + 1}

a_{i + 2})

intervallumba viszi, hiszen monotonitása miatt ha

\begin{matrix} a_{i} < x < a_{i + 1} \end{matrix}

akkor

\begin{matrix} φ (a_{i}) < φ (x) < φ (a_{i + 1}) . \end{matrix}

Emiatt, ha az

f_{n} (x)

függvényt csak az

(a_{n}, a_{n + 1})

zárt szakaszon tekintjük, azt ez a függvény, mivel a

φ

függvény inverzének

n

-szer egymás után való alkalmazását jelenti, a

(- 1, 1)

zárt szakaszra képezi le. Nevezetesen

\begin{matrix} f_{n} (a_{n}) = 1, f_{n} (a_{n + 1}) = - 1, \end{matrix}

(8)

ami

f_{n}

és

a_{n}

definíciójából teljes indukcióval közvetlenül következik, pl.:

\begin{matrix} f_{n} (a_{n}) = f_{n - 1} (f (a_{n})) = f_{n - 1} (a_{n - 1}) = 1. \end{matrix}

Hasonlóan indukcióval kapjuk, hogy az

f_{n} (x)

függvény az

(a_{n}, a_{n + 1})

szakaszon monoton fogy, tehát átmetszi az

y = x

egyenest. A kapott metszéspont abszcisszája lesz a (4) egyenlet keresett harmadik gyöke.

Göndőcs Ferenc

Megjegyzés. Az ábrán feltüntettük a (4) egyenlet

n = 2

-höz tartozó

b_{21}

és

n = 3

-hoz tartozó

b_{31}

gyökét, továbbá az (1) egyenletrendszer megfelelő

b_{21}, b_{22}

, ill.

b_{31}, b_{32}, b_{33}

, gyökrendszerét is.