Kezdőlap


Feladat:	Pontversenyen kívüli P.28	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beck József , Donga György , Gál Péter , Göndőcs Ferenc , Horváth Miklós , Reviczky János , Somorjai Gábor , Vajnági András
Füzet:	1969/december, 218 - 220. oldal		PDF \| MathML
Témakör(ök):	Inverzió, Körök, Síkgeometriai szerkesztések, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/március: Pontversenyen kívüli P.28

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel először, hogy $e$ és $f$ metszik egymást az $M$ pontban. Legyen $k$ tetszőleges, $r$ sugarú kör, középpontja $O$ , és $P$ a kerületének tetszőleges pontja. A $k$ -hoz $P$ -ben húzott érintővel $ε$ szöget bezáró ( $P$ -n átmenő) egyenes $O$ -tól mért $r_{1}$ távolsága független $P$ és az egyenes megválasztásától, hiszen $r$ átfogójú, $ε$ hegyesszöget tartalmazó derékszögű háromszög $ε$ melletti befogója. Hasonlóan legyen $r_{2}$ a $k$ -t $φ$ szögben metsző egyenesek $O$ -tól mért távolsága (1. ábra).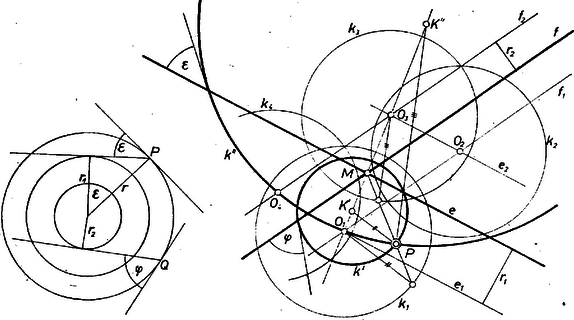

1. ábra 2. ábra

Egy

r

sugarú kör tehát akkor és csakis akkor metszi

e

-t

ε

f

-et

φ

szögben, ha középpontja

e

-től

r_{1}

f

-től

r_{2}

távolságra van. Négy ilyen pont van: az

e

-től

r_{1}

távolságra haladó

e_{1}

e_{2}

és az

f

-től

r_{2}

távolságra haladó

f_{1}

f_{2}

egyenesek által meghatározott paralelogramma csúcsai, legyenek ezek

O_{1}

O_{2}

O_{3}

O_{4}

. Tehát e négy pont körül

r

sugarú köröket rajzolva azok

e

-t

ε

f

-et

φ

szög alatt metszik; jelöljük ezeket

k_{1}

k_{2}

k_{3}

k_{4}

-gyel (2. ábra).
Ha

M

centrumú hasonlósággal a kapott köröket újabb körökbe visszük át, ezek az újabb körök is a megfelelő szögben metszik az egyeneseinket. Ilyen hasonlósággal pedig el tudjuk érni, hogy a körök

P

-n menjenek át. Annyi megfelelő kört kapunk, ahány metszéspont keletkezik az

M P

egyenesen, illetve az

M

-re való szimmetria miatt ezek a körök párosával megegyeznek, a megoldások száma tehát egyenlő a

k_{1}

és

k_{2}

köröknek az

M P

egyenesen levő metszéspontjainak a számával, ami

4

3

vagy

2

lehet.
Ha

e

és

f

párhuzamosak, és egy kör a megfelelő szögben metszi őket, akkor a kör középpontjának a tőlük mért távolságainak aránya megegyezik

r_{1} : r_{2}

-vel. E távolságok tehát, ha

e

és

f

távolsága

d

\begin{matrix} \frac{r_{1} d}{r_{1} + r_{2}}, \frac{r_{2} d}{r_{1} + r_{2}} vagy \frac{r_{1} d}{r_{1} - r_{2}}, \frac{r_{2} d}{r_{1} - r_{2}} \end{matrix}

aszerint, hogy a középpont a két egyenes között van-e vagy sem. (Itt feltettük, hogy

ε < φ

; az

ε = φ

esetben természetesen csak a két egyenes között lehet a középpont.) Ezek alapján szerkeszthetünk olyan köröket, amelyek az egyeneseket az adott szögben metszik, majd az

e

f

egyenesekkel párhuzamosan eltolva őket, elérhetjük, általában

2

-féleképpen, hogy

P

-n is átmenjenek.

Beck József

II. megoldás. Legyen

k

tetszőleges kör, melynek

P

a középpontja.

k

-ra invertálva¹ az

e

f

egyenesek

P

-n átmenő

k_{1}

k_{2}

körökbe mennek át, a keresett kör pedig olyan egyenesbe, mely

k_{1}

-et

ε

k_{2}

-t

φ

szögben metszi. A

k_{1}

-et

ε

szögben metsző egyenesek mind érintik a

k_{1}

-gyel koncentrikus

k'_{1}

kört (melyet tehát egy

k_{1}

-et

ε

szögben metsző, de különben tetszőlegesen felvett egyenes segítségével szerkeszthetünk meg). Hasonlóképpen kapjuk

k_{2}

-ből a

k'_{2}

kört: a keresett kör

x'

inverze tehát a

k'_{1}

és

k'_{2}

körök közös érintője, melyet

k

-ra invertálva megkapjuk a keresett

x

kört (3. ábra, a következő oldalon).

3. ábra

Mivel két kör közös érintőinek száma

4

3

2

1

vagy

0

, ennyi a keresett körök száma is.

Horváth Miklós (Veszprém, Lovassy L. Gimn., I. o. t. )

¹Lásd: Surányi János-Tusnády Gábor: Az inverzióról, K. M. L. 37 (1968) 97‐101. o.