Feladat: Pontversenyen kívüli P.21 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Beck József ,  Somorjai Gábor ,  Váli László 
Füzet: 1969/október, 71 - 73. oldal  PDF  |  MathML 
Témakör(ök): Ponthalmazok, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1969/február: Pontversenyen kívüli P.21

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel sem A intervallumainak, sem B-éinek nincs közös pontja, így a két rendszer közös részének minden egyes pontja A és B egy-egy meghatározott intervallumába esik. E két intervallum közös része egy intervallum, melynek kezdőpontja a két intervallum valamelyikének kezdőpontja, vagy a közös kezdőpontjuk, ha azok egybeesnek. Az utóbbi esetben rendeljük a közös rész részintervallumához az őt tartalmazó A-beli intervallumot, az előbbi esetben azt az A- vagy B-beli intervallumot, amelyikével a kezdőpontja egybeesik (1. ábra).

 

 

1. ábra
 

Így a közös részbeli különböző intervallumokhoz különböző intervallumokat rendeltünk, hiszen kezdőpontjaik különbözők, és bármely A- vagy B-beli intervallumot a közös résznek legfeljebb egy intervallumához rendeltünk hozzá. Így azonban az A és B első intervalluma közül az előbb kezdődőt, vagy ha kezdőpontjuk egybeesik, a B-belit nem rendeltük hozzá a közös rész egy intervallumához sem, ezért a közös rész legfeljebb 1-gyel kevesebb intervallumból állhat, mint amennyi A-ban és B-ben együtt van, vagyis n+m-1-ből.
Ennyiből viszont állhat, sőt jelöljük ki bárhogy az A- és B-beli intervallumok kezdőpontjait pl. úgy, hogy az elsők essenek egybe, a többiek viszont mind legyenek különbözők, és tartson minden intervallum az ugyanabba a halmazba tartozó következő kezdőpontig, az utolsó intervallumok pedig egy olyan végpontig, amelyiket az összes kezdőpont megelőz (2. ábra).
 

 

2. ábra*
 

Ekkor A is, B is, a közös rész is az első kezdőponttól az utolsó végpontig terjedő nyílt intervallum, elhagyva belőle az első esetben az A-beli, a második esetben a B-beli; a harmadik esetben az összes kezdőpontokat. Így valóban a 3 halmaz n, m, ill. m+n-1 intervallumból áll.
Ha A vagy B egyetlen intervallumot sem tartalmaz, akkor természetesen a közös részük sem; ezt az esetet a fentiekben kizártuk.
 

II. megoldás. Legyen a számegyenesen balról jobbra haladva az A halmaz j-edik szakaszának mj számú B-beli intervallummal nem üres közös része. Ekkor A∩B intervallumainak száma
k=m1+m2+...+mn.
Ennél az összeszámolásnál egy B-beli intervallumot 1-nél többször is számolhattunk, annyival többször, ahány A-beli szomszédos intervallumpárral van nem üres közös része. Mivel összesen n-1 ilyen szomszédos intervallumpár van, viszont lehetnek olyan B-beli intervallumok, amelyeket nem számoltunk, így azt kaptuk, hogy
k=m1+m2+...+mn≤m+n-1.
Itt egyenlőség is állhat, ha pl. n≥m, B l-edik intervalluma az A l-edik intervallumának utolsó harmadától l+1-edik intervallumának első harmadáig terjed l=1,...,m-1-re, B m-edik intervalluma pedig A m-edik intervallumának 2/3-ánál kezdődik és tartalmazza összes esetleges további szakaszát (3. ábra).
 

 

3. ábra*
 

Beck József (Budapest, I. István Gimn., III. o. t.)
 

III. megoldás. A közös rész két szomszédos intervallumát olyan pontok választják el (esetleg 1 pont), amelyek A és B közül legalább az egyikben nincsenek benne. Ezek a pontok együtt a számegyenes A-ba nem tartozó pontjainak ‐ az A-hoz a számegyenesre vonatkozóan tartozó kiegészítő (komplementer) halmaznak, szokásos jelével A¯-nak ‐ és a B-be nem tartozó pontok B¯ halmazának az egyesítése: A¯∪B¯. Ez éppen A∩B komplementere:
A∩B¯=A¯∪B¯.
Ha A az (ai,bi) i=1,...,n intervallumokból áll (a1<b1≤a2< <b2...an-1<bn-1≤an<bn, akkor A¯ az a1-ig terjedő és a bn-től kezdődő félegyenesből és a [bi,ai+1] zárt intervallumokból áll (i=1,...,n-1), amelyek egy-egy pontra is redukálódhatnak (4. ábra).
 

 

4. ábra
 

Hasonlóan B¯ két félegyenesből és m-1 zárt intervallumból áll.
Az A¯∪B¯ ugyancsak két félegyenesből és zárt szakaszokból áll. Az utóbbiak számát jelöljük k-val. A¯∪B¯ nyilván legfeljebb annyi szakaszból áll, mint A¯ és B¯ együtt, azaz
k≤m+n-2,
mert az egyesítésnél több intervallum alkothat egy nagyobbat, de új intervallum nem keletkezhet. A k intervallum közt A∩B-nek k-1 intervalluma van, ezen kívül az első félegyenes és az első szakasz, továbbá az utolsó szakasz és a második félegyenes közt egy-egy, így A∩B intervallumainak száma
k+1≤m+n-1.

Itt az egyenlőség bekövetkezhet pl. ha A első szakasza tartalmazza B első m-1 szakaszát és még az utolsóval is van nem üres közös része, B utolsó szakasza pedig tartalmazza A többi szakaszait. Ekkor ugyanis A¯ és B¯ szakaszainak sem egymással, sem a félegyenesekkel nincs közös pontja (5. ábra).
 

 

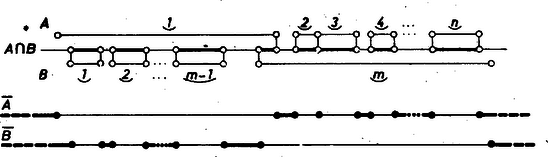5. ábra
 
*A 2. ábra kiegészítendő: a bal szélén alul is kell osztásvonal.

*A 3. ábrán m+1 és n közé 3 pont teendő.