Kezdőlap


Feladat:	Pontversenyen kívüli P.15	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csirmaz László , Váli LÁszló
Füzet:	1969/szeptember, 25 - 28. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Szabályos sokszögek szerkesztése, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1968/december: Pontversenyen kívüli P.15

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy a szerkesztés pontos, $α = 2 π / 17$ jelöléssel 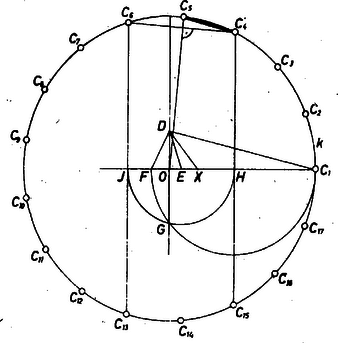$C_{1} O C_{4} ∢ = 3 α$ és $C_{1} O C_{6} ∢ = 5 α$ .

Válasszuk hosszúságegységnek a

k

kör sugarát. Így

cos C_{1} O C_{4} ∢ = O H

és

cos C_{1} O C_{6} ∢ = O J

, pozitívnak véve az

O C_{1}

irányt, és meg kell határoznunk

cos 3 α

-t és

cos 5 α

-t.
Kiindulunk a

\begin{matrix} cos n α = cos α cos (n - 1) α - sin α sin (n - 1) α \end{matrix}

összefüggésből. Ezt az

n = 1,2, ...,17

értékekre felírva és összeadva

\begin{matrix} cos α + cos 2 α + cos 17 α = \\ = cos α (1 + cos α + cos 2 α + ... + cos 16 α) - sin α (sin α + sin 2 α + ... + sin 16 α) . \end{matrix}

A második zárójel értéke

0

, hiszen

sin n α + sin (17 - n) α = 0

, így pedig az első zárójel értéke is

0

, hiszen

cos 17 α = 1

folytán egyenlő a bal oldallal, és szorzója,

cos α \neq 1

. Így

\begin{matrix} cos α + cos 2 α + ... + cos 16 α = - 1, \end{matrix}

ami a

\begin{matrix} t_{n} = cos n α + cos (17 - n) α = 2 cos n α \end{matrix}

jelölés bevezetésével így alakul:

\begin{matrix} t_{1} + t_{2} + ... + t_{8} = - 1. \end{matrix}

(1)

A bevezetett számokra egyrészt nyilvánvalóan

\begin{matrix} t_{n} = t_{- n} & = t_{17 - n}, & (2) \\ t_{n} \cdot t_{m} = t_{n - m} & + t_{n + m}, & (3) \end{matrix}

másrészt mint könnyen belátható,

\begin{matrix} 2 > t_{1} > t_{2} > 2 cos 60^{\circ} = 1 > t_{3} > t_{4} > 0 > t_{5} > t_{6} > t_{7} > t_{8} > - 2. \end{matrix}

(4)

Tekintsük most a következő két összeget:

\begin{matrix} U = t_{1} + t_{2} + t_{4} + t_{8}, u = t_{3} + t_{5} + t_{6} + t_{7}, \end{matrix}

ezekre (1)‐(3) alapján a következő egyenletrendszert kapjuk:

\begin{matrix} U + u = - 1, U \cdot u = 4 (t_{1} + t_{2} + ... + t_{8}) = - 4, \end{matrix}

(5)

tehát a másodfokú egyenlet gyökei és együtthatói közti összefüggések alapján

\begin{matrix} U = \frac{- 1 + \sqrt[]{17}}{2}, u = \frac{- 1 - \sqrt[]{17}}{2}, \end{matrix}

(6)

ugyanis (4) miatt

U > 0

.
Ezek alapján hasonlóan számíthatjuk ki a következő két-két összeget:

\begin{matrix} V = t_{1} + t_{4}, v = t_{2} + t_{8}; w = t_{3} + t_{5}, W = t_{6} + t_{7}, \end{matrix}

ugyanis ezekre

\begin{matrix} V + v = U és V \cdot v = - 1, illetőleg w + W = u és w \cdot W = - 1, \end{matrix}

és mivel még (4) szerint

V > 0

és

W < 0

, azért

\begin{matrix} v = \frac{U - \sqrt[]{U^{2} + 4}}{2}, & (7) \\ w = \frac{u + \sqrt[]{u^{2} + 4}}{2} . & (8) \end{matrix}

Végül a

w

összeg tagjainak szorzata (3) szerint

\begin{matrix} t_{3} t_{5} = t_{2} + t_{8} = v, \end{matrix}

így a keresett két érték

2

-szerese:

2 cos 3 α = t_{3}

és

2 cos 5 α = t_{5}

a következő másodfokú egyenlet két gyöke:

\begin{matrix} x^{2} - w x + v = 0, \end{matrix}

(9)

előrebocsátott megjegyzésünk szerint azt kell tehát megvizsgálnunk, hogy az előjeles

O H

O J

szakaszok

2

-szerese is kielégíti-e (9)-et.
A szerkesztés szerint

O D = 1 / 4

D C_{1} = \sqrt[]{17} / 4

. Legyen

X

O D C_{1}

háromszög

D

-beli szögfelezőjének

O C_{1}

-gyel való metszéspontja. A szögfelező-tétel alkalmazásával, majd felismerve a (6)-beli második kifejezést, továbbá az

O D X

derékszögű háromszögből

\begin{matrix} O X = \frac{O D \cdot O C_{1}}{O D + O C_{1}} = \frac{\frac{1}{4}}{\frac{1}{4} + \frac{\sqrt[]{17}}{4}} = - \frac{1}{2 u}, \\ D X = \sqrt[]{O D^{2} + O X^{2}} = - \frac{1}{4 u} \sqrt[]{u^{2} + 4} . \end{matrix}

Hasonlóan, mivel

D E

O D X

háromszög szögfelezője, mindjárt felismerve a (8) kifejezést

\begin{matrix} O E = \frac{O D \cdot O X}{O D + D X} = \frac{- \frac{1}{4} \cdot \frac{1}{2 u}}{\frac{1}{4} - \frac{1}{4 u} \sqrt[]{u^{2} + 4}} = \frac{1}{2 (\sqrt[]{u^{2} + 4} - u)} = & (10) \\ = \frac{1}{4} \cdot \frac{u + \sqrt[]{u^{2} + 4}}{2} = \frac{w}{4}, \end{matrix}

és ebből

\begin{matrix} tg E D O ∢ = \frac{O E}{O D} = w . \end{matrix}

Ennek alapján kifejezhetjük

O F

-et. (8) és (5) felhasználásával, majd felismerve a (7) kifejezést

\begin{matrix} O F = - O D tg (45^{\circ} - E D O ∢) = - \frac{1}{4} \cdot \frac{1 - w}{1 + w} = - \frac{1}{4} \cdot \frac{(2 - u) - \sqrt[]{u^{2} + 4}}{(2 + u) + \sqrt[]{u^{2} + 4}} = & (11) \\ = \frac{2 - \sqrt[]{u^{2} + 4}}{- 4 u} = \frac{2 U - \sqrt[]{{(u U)}^{2} + 4 U^{2}}}{- 4 u U} = \frac{1}{4} \cdot \frac{U - \sqrt[]{U^{2} + 4}}{2} = \frac{v}{4} . \end{matrix}

Most már képezhetjük a kérdéses

2 O H

2 O J

előjeles szakaszok összegét és szorzatát.

E

felezi a

J H

szakaszt, ezért (10) alapján

\begin{matrix} \frac{O H + O J}{2} = O E, 2 O H + 2 O J = 4 O E = w, \end{matrix}

(12)

a közös magasságú

H J G

és

G_{1} F G

derékszögű háromszögekből pedig (11) alapján

\begin{matrix} 2 O H \cdot 2 O J = - 4 O H \cdot | O J | = - 40 G^{2} = - 4 \cdot O C_{1} \cdot | O F | = 4 \cdot O F = v, \end{matrix}

(13)

és (12), (13) együtt azt jelenti, hogy az

O H

O J

előjeles szakaszok

2

-szerese szintén kielégíti a (9) egyenletet. És mivel (9)-nek csak két gyöke van, a két úton kapott gyökök páronként azonosak, (4) figyelembevételével

\begin{matrix} 2 O H = t_{3} = 2 cos 3 α, 2 O J = t_{5} = 2 cos 5 α, \end{matrix}

ami állításunkat bizonyítja.

Csirmaz László (Budapest, I. István Gimn., IV. o. t. )

Megjegyzés. C. F. Gauss német matematikus bebizonyította (19 éves korában, 1796-ban), hogy szabályos sokszög eukleidészi szerkesztéssel akkor és csak akkor szerkeszthető, ha oldalai számának prímfelbontása

2^{m} \cdot p_{1} \cdot p_{2} ... \cdot p_{r}

alakú, ahol

p_{1}, ..., p_{r}

egymástól különböző,

2^{s} + 1

alakú prímek,

s = 2^{t}

alakú kitevővel. (A

t = 0

és

1

esetek, szabályos háromszög és szabályos ötszög, közismertek.) Azóta számos eljárást adtak meg a szabályos

17

-szög szerkesztésére, a fentiekben H. W. Richmond eljárását ismertük meg (1893). Az

α = 2 π / 17

szögre Gauss a következő eredményt közölte egy tanítványával:

\begin{matrix} cos α = - \frac{1}{16} + \frac{\sqrt[]{17}}{16} + \frac{1}{16} \sqrt[]{34 - 2 \sqrt[]{17}} + \\ + \frac{1}{8} \sqrt[]{17 + 3 \sqrt[]{17} - \sqrt[]{34 - 2 \sqrt[]{17}} - 2 \sqrt[]{34 + 2 \sqrt[]{17}}} . \end{matrix}