Feladat: Pontversenyen kívüli P.14 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Beck József ,  Csirmaz László 
Füzet: 1969/május, 216 - 217. oldal  PDF  |  MathML 
Témakör(ök): Numerikus és grafikus módszerek, Numerikus módszerek, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1968/december: Pontversenyen kívüli P.14

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megadott t0, értékek mellett a sorozatok első értékeit az alábbi táblázat tartalmazza:

 

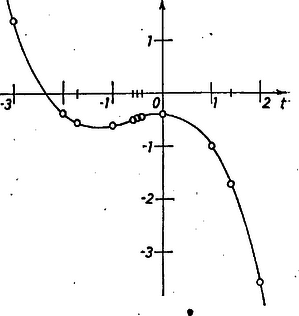
t01 -3 -2 -1 -1/2   0   1   2t11 +1,4 -0,4 -0,6 -0,475-0,4 -1 -3,6t21 -1,73 -0,4512 -0,5007 -0,4512 -0,6 +3,7472t31 -0,562

Ezek alapján ábrázoljuk az f(t)=-15(t3+2t2+2) függvényt.
 

 

Mivel t=-0,4 mellett f(t)<t és t=-0,5 mellett f(t)>t, a t=f(t) egyenletnek van a (-0,5;-0,4) számközben gyöke, jelöljük ezt t*-gal:
-0,5<t*<-0,4.(2)
Legyen tn=t*+ε, akkor (1) alapján
tn+1=-15[(t*3+2t*2+2)+ε(3t*2+4t*)++ε2(3t*+2)+ε3]=t*+ε5(A+Bε-ε2),


ahol A=-3t*2-4t*;B=-3t*-2. (Felhasználtuk, hogy t* gyöke az egyenletnek, azaz f(t*)=t*.) (2) alapján ‐ mivel e számközben A monoton ‐
1,12<A<1,25,(3)-0,8<B<-0,5.(4)


Megmutatjuk, hogy ha -1≤tn≤0, akkor tn-től kezdve a sorozat monoton, mégpedig tn<t* esetén monoton növekvő és tn>t* mellett monoton fogyó. (2) miatt ugyanis ekkor |ε|<0,6, tehát (3), (4) alapján
A+Bε-ε2<A+|B|⋅|ε|<1,25+0,6⋅0,8=1,73<2,A+Bε-ε2>A-|B|⋅|ε|-ε2>1,12-0,48-0,36=0,28>0.
Ezek alapján pedig
0<tn+1-t*tn-t*<0,4,(5)
vagyis tn+1 a t* gyöknek ugyanazon az oldalán van, mint tn, de közelebb kerül a gyökhöz, a hiba határozottan csökken. Ez utóbbi megállapításból következik, hogy tn+1 is a (-1,0) számközben van, tehát a fenti tulajdonság az összes további lépésnél megmarad.
A t0=2 kiinduló érték kivételével az összes többi sorozat az első néhány lépés során bejut a (-1,0) számközbe, és ettől kezdve monoton lesz. Mivel a hiba minden lépésben az előző hiba felénél kisebbre csökken, ezekben a sorozatokban a t* gyök tetszőlegesen jó közelítése megtalálható.
A t0=2 kezdeti értékből kiindulva egyre nagyobb abszolút értékű számokat kapunk váltakozó előjellel a sorozat elemeire. Megmutatjuk, hogy ez mindig így van, ha a hiba legalább 3, azaz |ε|≥3.
A+Bε-ε2<-ε2(1-Bε-Aε2)<-ε2(1-0,53-1,259)<-6,tn+1-t*tn-t*<-1,2.


Tehát ha a hiba 3-nál nagyobb, akkor minden lépésben megváltozik az előjele, és abszolút értékben növekszik.
 

 Beck József, Csirmaz László